3.0 Gegeben ist die Funktion $k:x \mapsto \frac{x^2}{4\ln(2x + 4)}$, ihre Ableitungsfunktion k' und die Funktion $h:x \mapsto \frac{1}{k(x)}$ jeweils in ihren maximalen reellen Definitionsmengen.

3.1 Zeigen Sie rechnerisch, dass für die Funktion k gilt: $\mathbb{D}_k=\left] ; \infty \right[ \setminus \left\{-1{,}5\right\}$. (3 BE)

3.2 Ordnen Sie jedem Graphen der Bilder $a$, $b$ und $c$ einer der Funktionen $k$, $k'$ oder $h$ zu und begründen Sie Ihre Wahl. (4 BE)

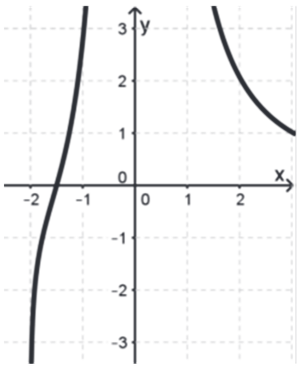
Bild a

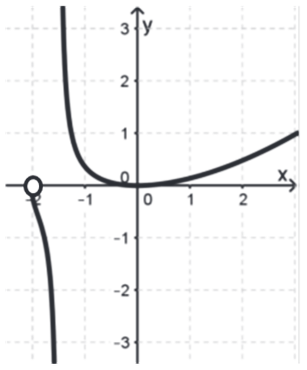
Bild b

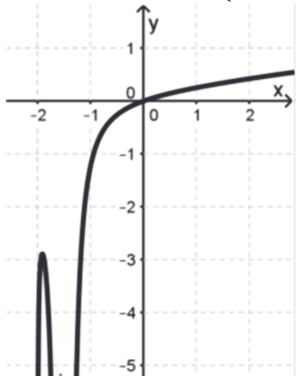
Bild c

3.3 Untersuchen Sie das Verhalten der Funktionswerte von $k(x)$ für $x \rightarrow \infty$. (2 BE)