A II

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die reelle Funktion $f : x \mapsto \frac{2 x + 1}{x^{3}}$ mit der maximalen Definitionsmenge $𝔻_{f} \subset ℝ$ . Ihr Graph wird mit $G_{f}$ bezeichnet.
1. Geben Sie $𝔻_{f}$ und die Art der Definitionslücke von $f$ an und bestimmen Sie die Nullstelle von $f$ . (3 BE)
2. Untersuchen Sie das Verhalten der Funktionswerte an den Rändern von $𝔻_{f}$ und geben Sie Art und Gleichungen aller Asymptoten von $𝔾_{f}$ an. (5 BE)
3. Ermitteln Sie die maximalen Monotonieintervalle von $𝔾_{f}$ und bestimmen Sie Art und Koordinaten des Extrempunktes von $𝔾_{f}$ . (7 BE)
  $[Mögliches Teilergebnis: f^{'} (x) = \frac{- 4 x - 3}{x^{4}}]$
4. Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und mittels geeigneter zusätzlicher Funktionswerte $G_{f}$ für $- 5 \leq 5 x \leq 5$ in ein kartesisches Koordinatensystem (5 BE)
5. Zeigen Sie, dass sich der Funktionsterm $f (x)$ auch durch $f (x) = \frac{2}{x^{2}} + \frac{1}{x^{3}}$ darstellen lässt und bestimmen Sie seine Stammfunktion F der Funktion f mit $𝔻_{F} = 𝔻_{f}$ . (3 BE)
6. Der Graph $G_{f}$ , die Geraden $x = 1, x = b (b > 1)$ und die x-Achse schließen ein Flächenstück ein. Kennzeichnen Sie dieses Flächenstück für $b = 4$ im Koordinatensystem der Teilaufgabe 1.4. Zeigen Sie, dass sich für die Maßzahl des Flächeninhalts $A (b) = - \frac{2}{b} - \frac{0,5}{b^{2}} + 2,5$ ergibt. Bestimmen Sie den Grenzwert von A(b) für $b \to \infty$ . (6 BE)
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Zum Ende des Jahres 1995 (Zeitpunkt $t = 0$ ) lebten laut der Organisation der Vereinten Nationen (UNO) 5,74 Milliarden Menschen auf der Erde. Ende 2016 hatte die Erdbevölkerung gegenüber $t = 0$ um $29,1 %$ zugenommen. Mit der vereinfachenden Annahme einer exponentiellen Entwicklung gilt für die Gesamtzahl $N$ der Weltbevölkerung in Milliarden in Abhängigkeit von der Zeit $t$ in Jahren die Gleichung $N (t) = a \cdot e^{b t}$ mit $t \geq 0$ und $a, b \in ℝ$ . Runden Sie Ihre Ergebnisse sinnvoll.
1. Bestimmen Sie aus den obigen Angaben die Parameter $a$ und $b$ . $[Ergebnisse: a \approx 5,74; b \approx 0,01216]$ (4 BE)
2. Berechnen Sie, wie viele Menschen zum Ende des Jahres 2005 nach dem Modell von 2.0 auf der Erde lebten. Vergleichen Sie das Ergebnis mit der tatsächlichen Weltbevölkerung Ende 2005 von 6,52 Milliarden (UNO), indem Sie die prozentuale Abweichung berechnen und bewerten Sie damit die Güte des Modells. Geben Sie außerdem stichpunktartig drei Gründe an, die eine genaue Ermittlung der weltweiten Bevölkerungszahl erschweren. (6 BE)
3. Ermitteln Sie, um wie viele Menschen die Weltbevölkerung voraussichtlich im Jahr 2017 zunehmen wird. (2 BE)
4. Bestimmen Sie die Gleichung der Ableitungsfunktion $\dot{N}$ und berechnen Sie $\dot{N} (21)$ .Interpretieren Sie diesen Wert im Sachzusammenhang und vergleichen Sie ihn mit Ihrem Ergebnis der Teilaufgabe 2.3. (4 BE)
5. Bestimmen Sie das Jahr, in dem sich die Weltbevölkerung gegenüber dem 31.12.1995 nach dem Modell von 2.0 verdoppelt haben wird. (3 BE)
6. Berechnen Sie, welche Bevölkerungszahl sich am Ende des Jahres 2052 ergeben würde, wenn man - in einem anderen Szenario - ab Ende des Jahres 2016 von einer linearen Zunahme um 90 Mio. pro Jahr ausgeht. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Multiplikation
  1. von 1995 bis 2016 sind es 21 Jahre.
  Nach dem Modell werden also Ende 2016 etwa $5,74 \cdot e^{0,01216 \cdot 16} \approx 7,41$ Milliarden Menschen auf der Erde leben.
  2. Es kommen $2052 - 2016 = 36$ Jahre dazu.
  3. $36 \cdot 90 = 3240 Millionen$ . Es kommen also $3,24$ Milliarden Menschen dazu.
  4. Es leben dann etwa $7,41 + 3,24 = 10,65$ Milliarden Menschen auf der Erde.
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  1. Ausrechnen wie viele Menschen $2016$ auf der Erde leben
  2. Berechnen, wie viele weitere Jahre bis $2052$ dazukommen werden
  3. Lösung aus 2. mit jährlich $90$ Millionen multiplizieren (Ergebnis in Milliarden umrechnen)
  4. Ergebnis von 3. mit Ergebnis von 1. addieren
3
3.0 Gegeben ist die Funktion $k : x \mapsto \frac{x^{2}}{4 \ln (2 x + 4)}$ , ihre Ableitungsfunktion k' und die Funktion $h : x \mapsto \frac{1}{k (x)}$ jeweils in ihren maximalen reellen Definitionsmengen.
3.1 Zeigen Sie rechnerisch, dass für die Funktion k gilt: $𝔻_{k} =]; \infty [∖ {- 1,5}$ . (3 BE)
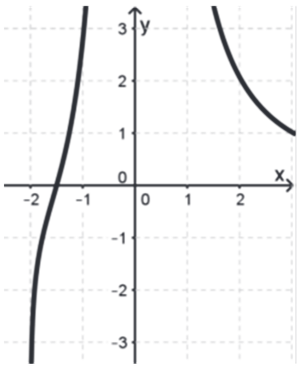
3.2 Ordnen Sie jedem Graphen der Bilder $a$ , $b$ und $c$ einer der Funktionen $k$ , $k^{'}$ oder $h$ zu und begründen Sie Ihre Wahl. (4 BE)
Bild a
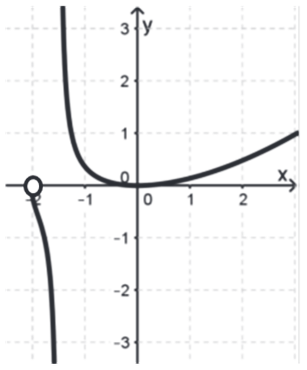
Bild b
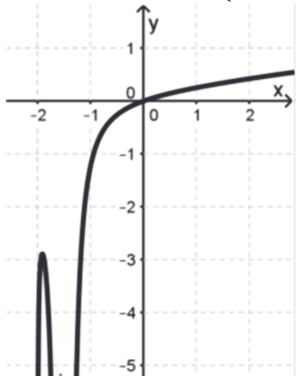
Bild c
3.3 Untersuchen Sie das Verhalten der Funktionswerte von $k (x)$ für $x \to \infty$ . (2 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

A II

Hast du eine Frage oder Feedback?