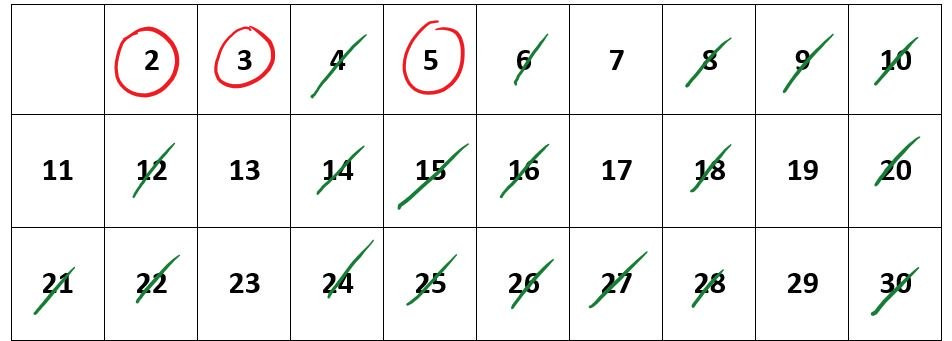
Beim Ermitteln der Primzahlen nach dem Sieb des Eratosthenes lässt sich folgendes feststellen: Die Verfahrensschritte müssen in einer Liste nur für alle Primzahlen mit angewendet werden. Denn die Vielfachen von Primzahlen mit sind bereits durchgestrichen.
Erkläre diesen Zusammenhang!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?