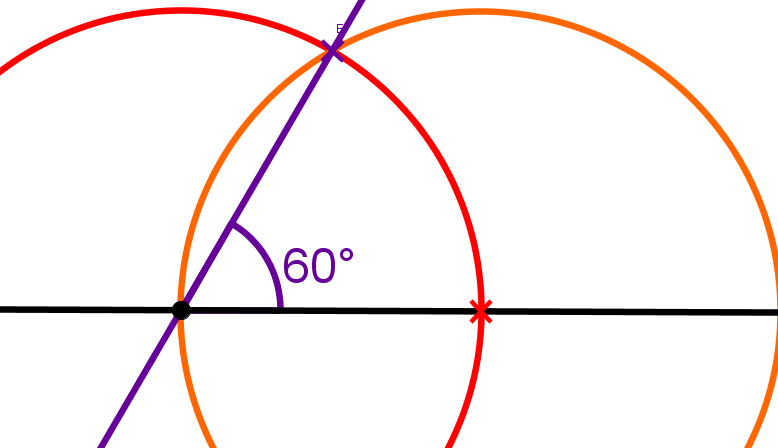Konstruiere einen 52,5° - Winkel nur mit Zirkel und Lineal.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel konstruieren
In konstruierbare Teilwinkel aufteilen
Mathematisch lässt sich der 52,5°- Winkel durch andere Winkel ausdrücken. Diese Umformungen führen auf 60° und 90° zurück.
| 52,5° | ||
| = | 30°+22,5° | |
| = | 21⋅60°+21⋅45° | |
| = | 21⋅60°+21⋅21⋅90° |
Der 90°- und der 60°- Winkel und ihre Hälften sind konstruierbar. 52,5° kann also aus einer Kombination dieser Winkel und einiger Winkelhalbierungen konstruiert werden.
Winkel konstruieren
Konstruiere die Winkelhalbierende und erhalte somit einen 30° Winkel.
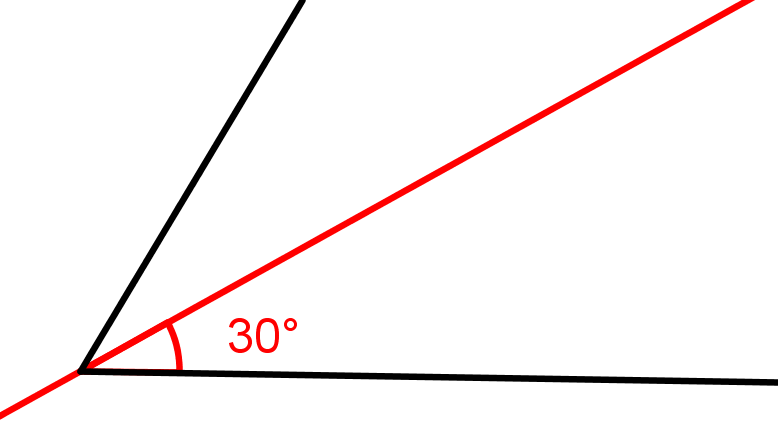
Konstruiere auf dem oberen Schenkel des 30° Winkels ein Lot, welches auch durch den Scheitelpunkt geht.
Konstruiere die Winkelhalbierende des 90° Winkels (des Lots !), und erhalte somit einen 45° Winkel.
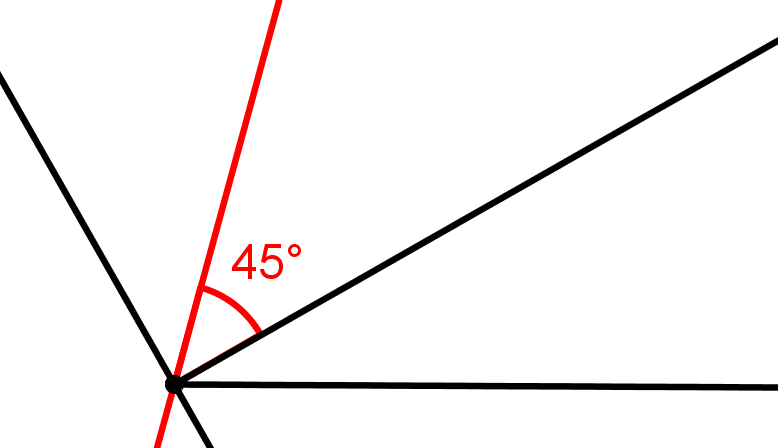
Konstruiere die Winkelhalbierende des 45° Winkels, und erhalte somit einen 22,5° Winkel.
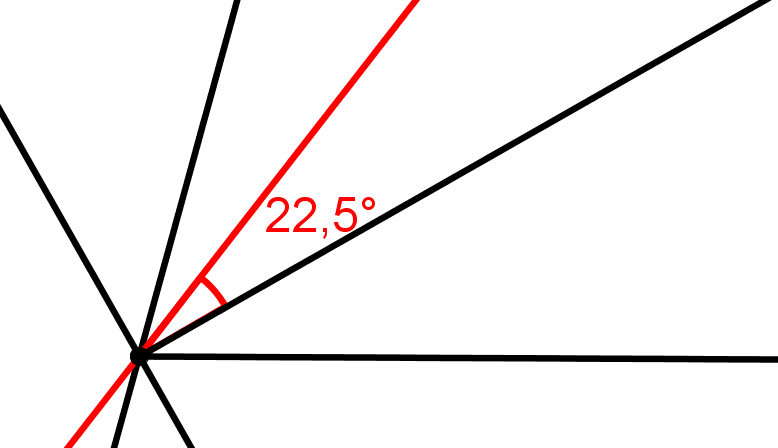
Der 52,5°- Winkel hat nun die erste Gerade und die eben konstruierte Winkelhalbierende als Schenkel.
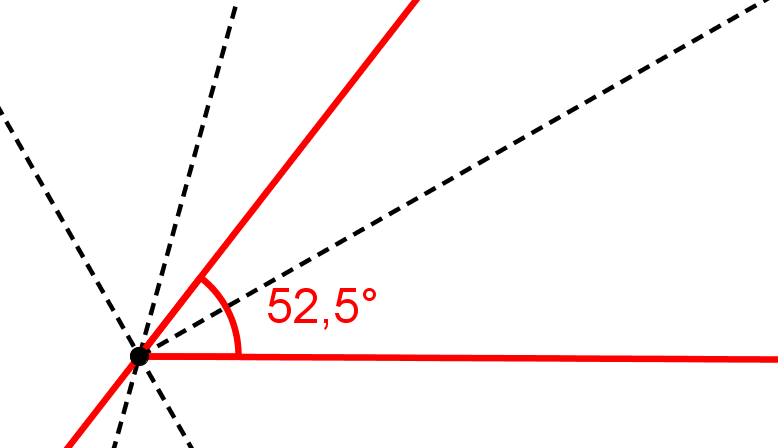
Winkel wie 90° und 60° sind konstruierbar. Außerdem können Winkel geometrisch halbiert werden. Überlege, wie sich aus 90°, 60° bzw. Hälften davon der Winkel 52,5° bilden lässt.
