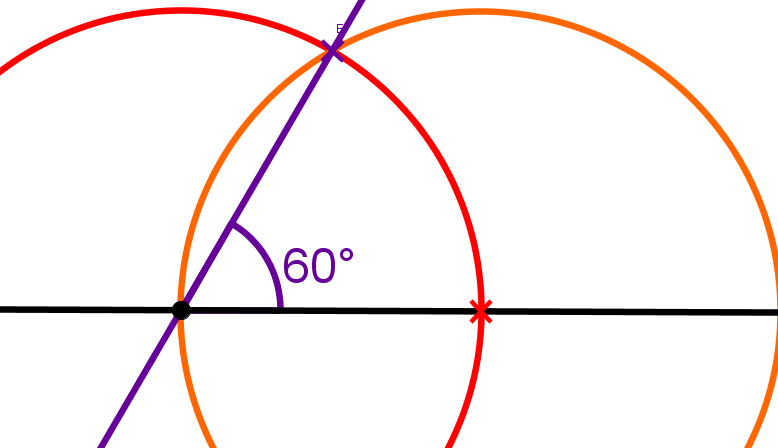Aufgaben zur Konstruktion von geometrischen Objekten
Hier findest du Aufgaben zur Konstruktion von Strecken, Winkeln und Formen. Schaffst du sie alle?
- 1

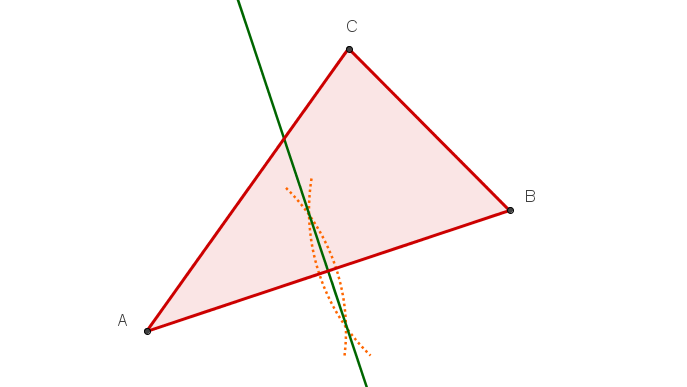
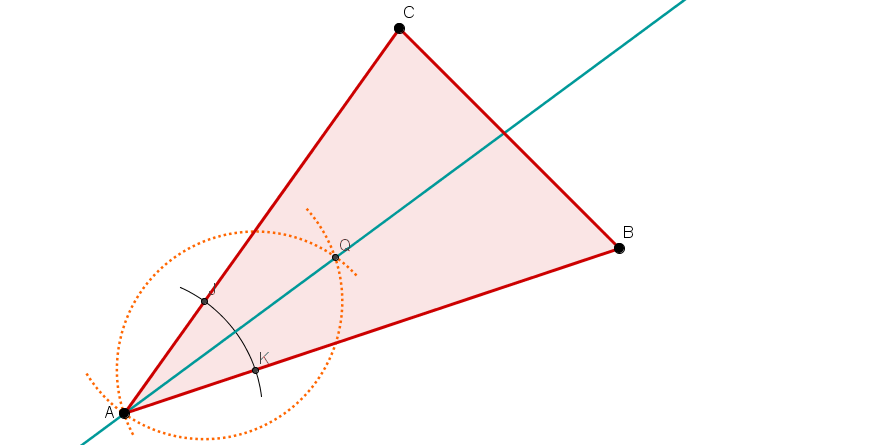
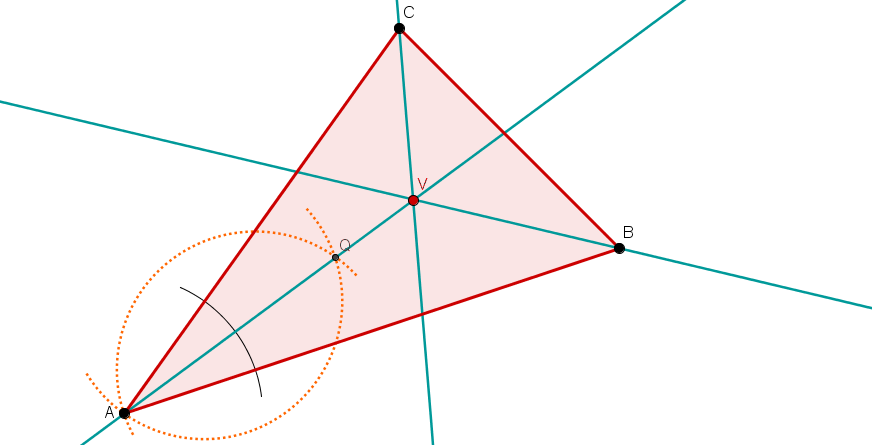
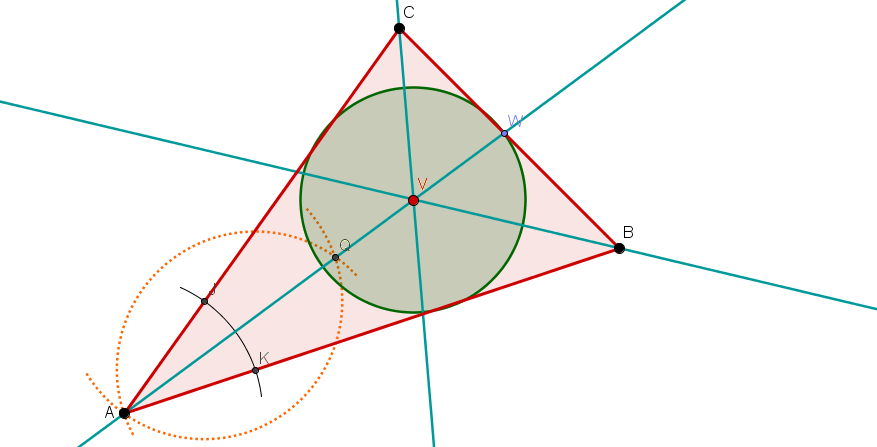
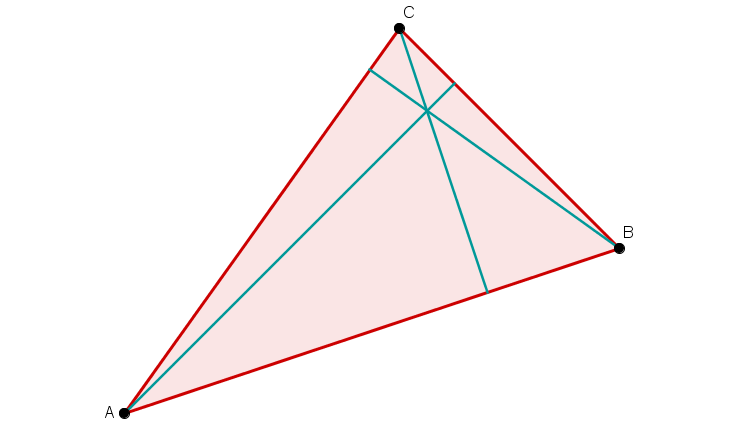
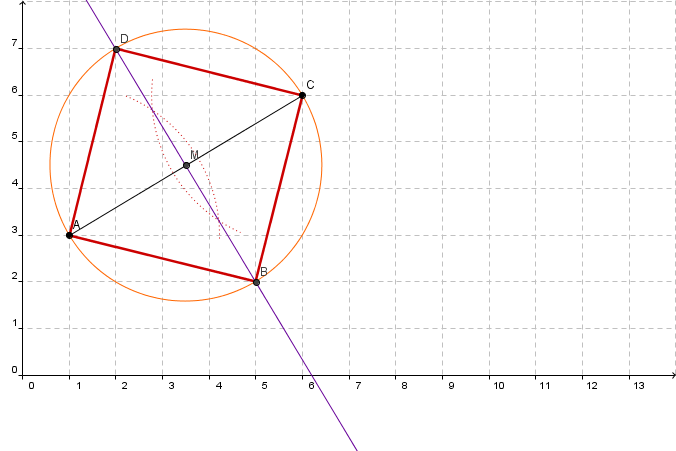
Zeichne ein beliebiges Dreieck (wie im Bild rechts).
Konstruiere dann nacheinander folgende Linien:
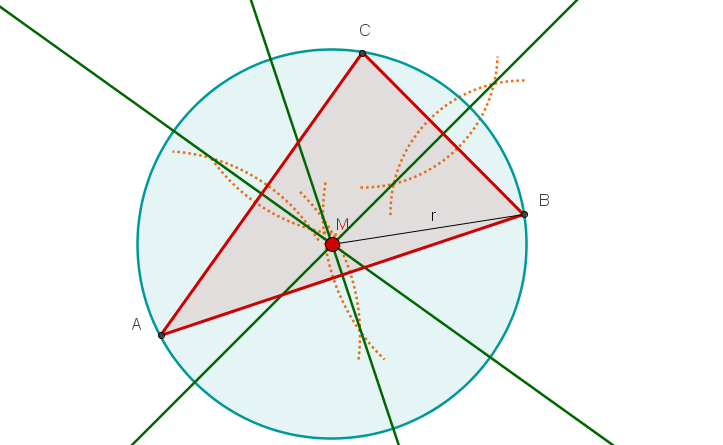
Alle drei Mittelsenkrechten und den Umkreis.
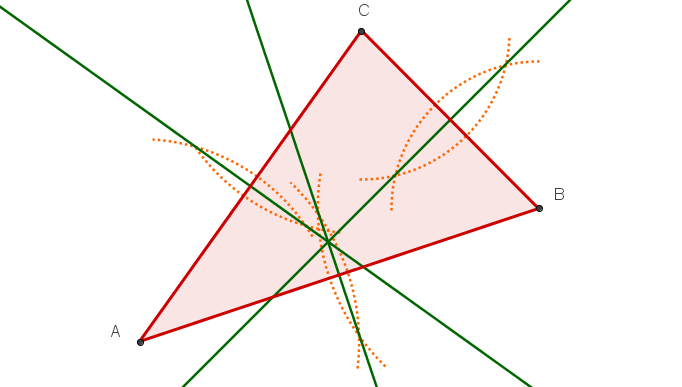
Alle drei Winkelhalbierenden und den Inkreis
Alle drei Höhen.
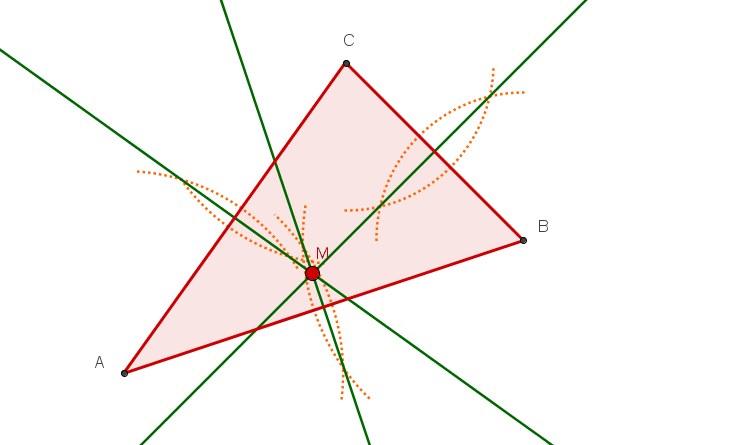
Alle drei Seitenhalbierenden.
- 2
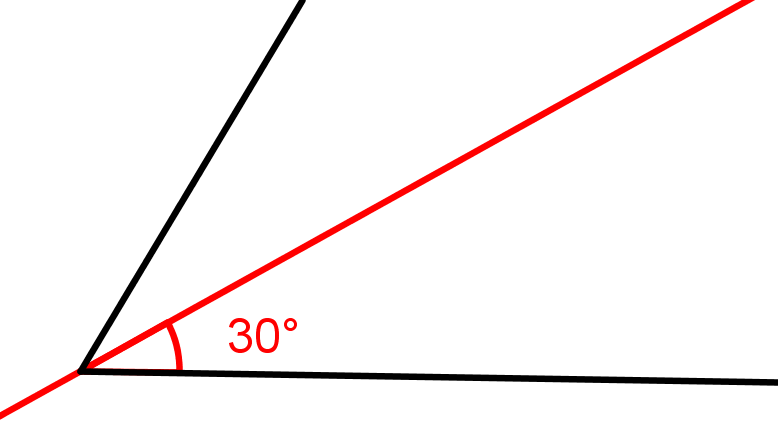
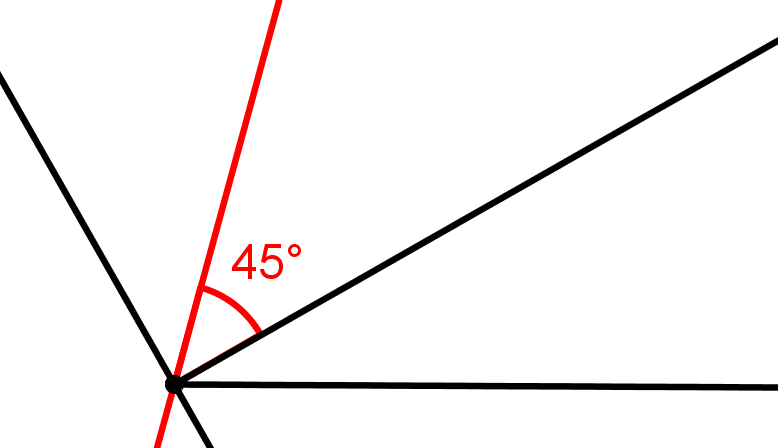
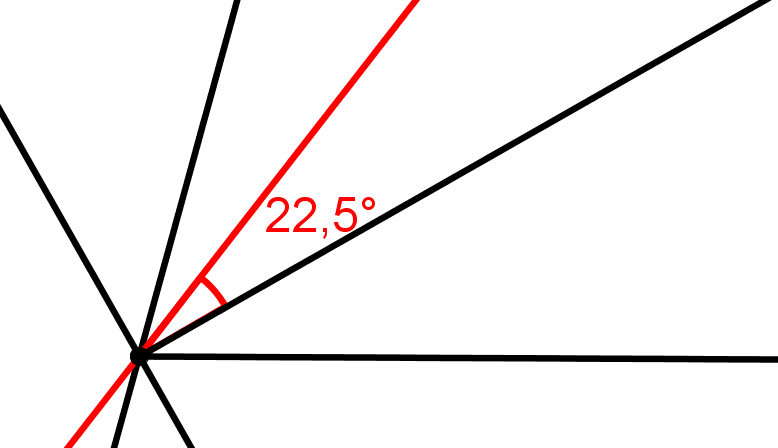
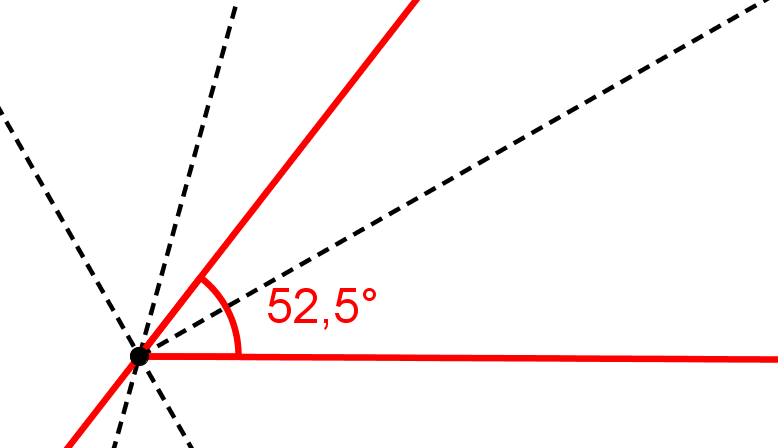
Konstruiere einen - Winkel nur mit Zirkel und Lineal.
- 3
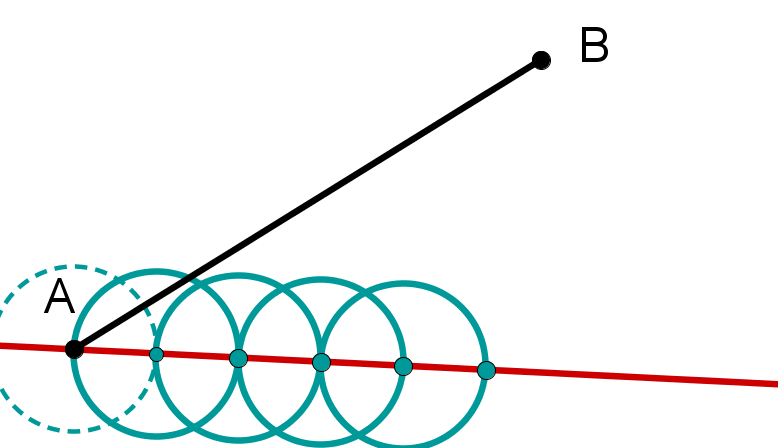
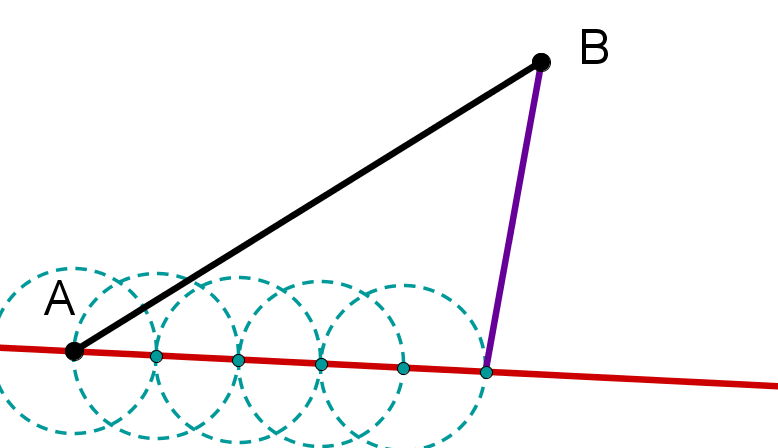
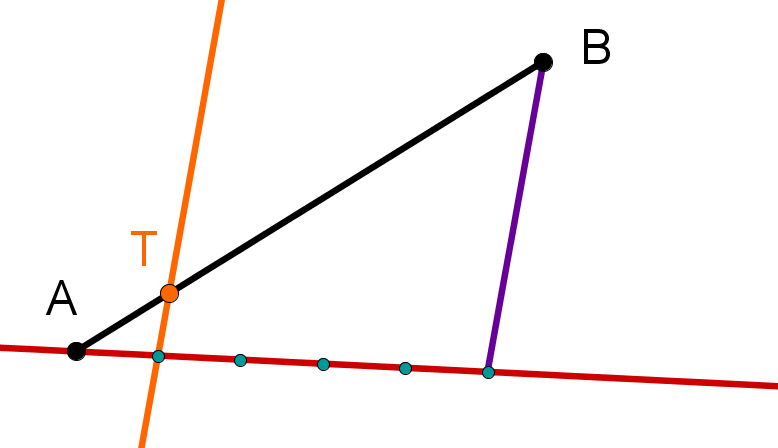
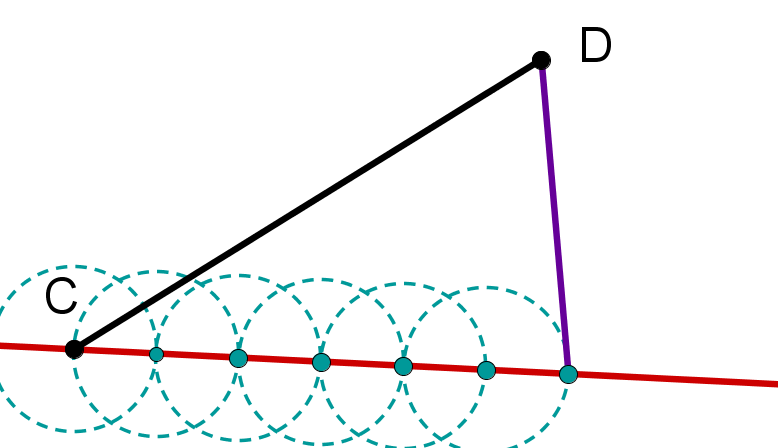
Teile die Strecken im angegebenen Verhältnis und bestimme die Längen der Teilstrecken.
im Verhältnis 1:4
im Verhältnis 4:2
- 4
Das Quadrat ist durch die Koordinaten von und eindeutig festgelegt.

Konstruiere die fehlenden Punkte und . Zeichne das Quadrat.
Berechne den Schnittpunkt der Diagonalen und gib ihn in das Eingabefeld ein.
Punkte kannst du wie "(3;-2,5)" in das Eingabefeld eingeben.
- 5

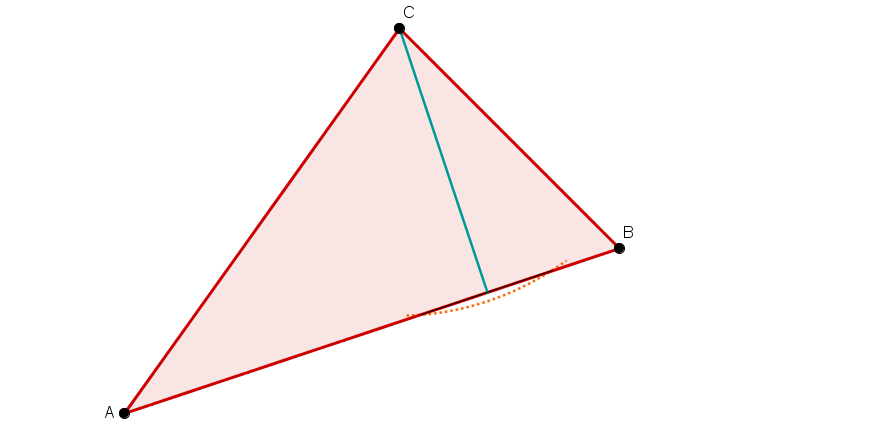
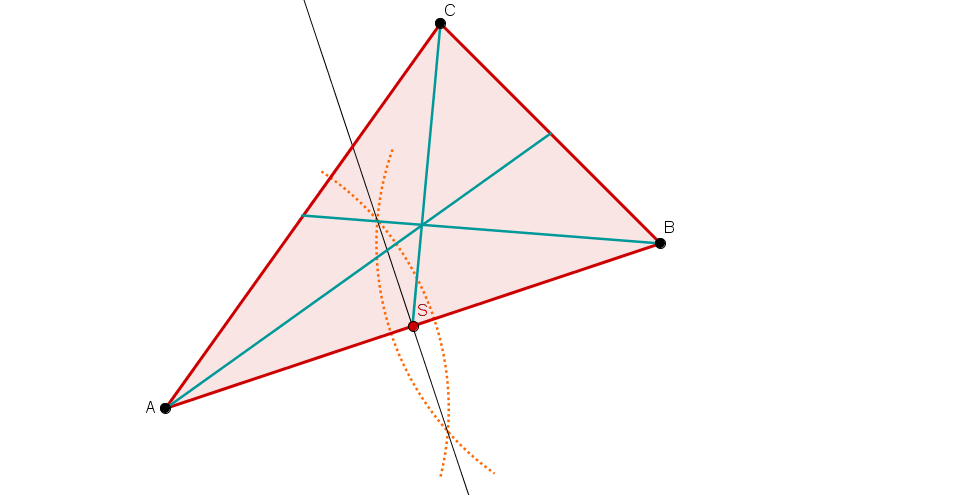
Zeichne ein beliebiges Dreieck (wie im Bild rechts).
Konstruiere dann nacheinander folgende Linien:
Alle drei Mittelsenkrechten und den Umkreis.
Alle drei Winkelhalbierenden und den Inkreis.
Alle drei Höhen.
Alle drei Seitenhalbierenden.
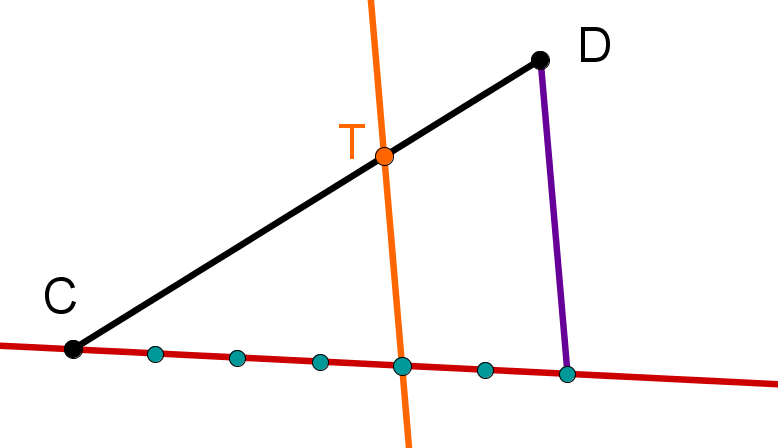
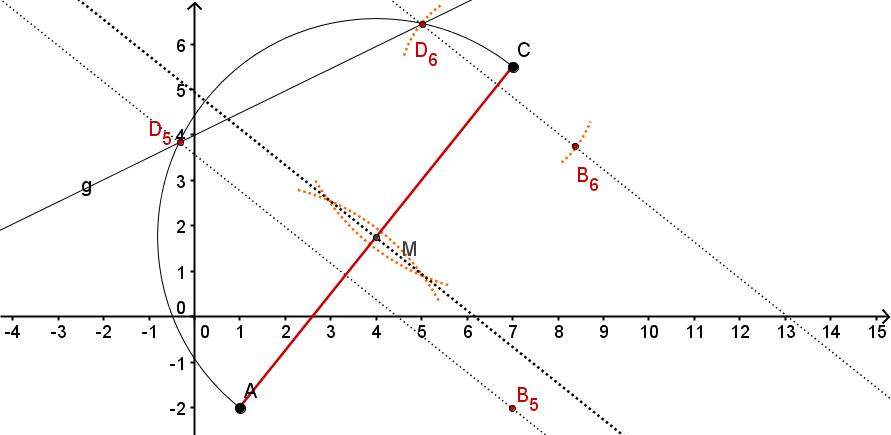
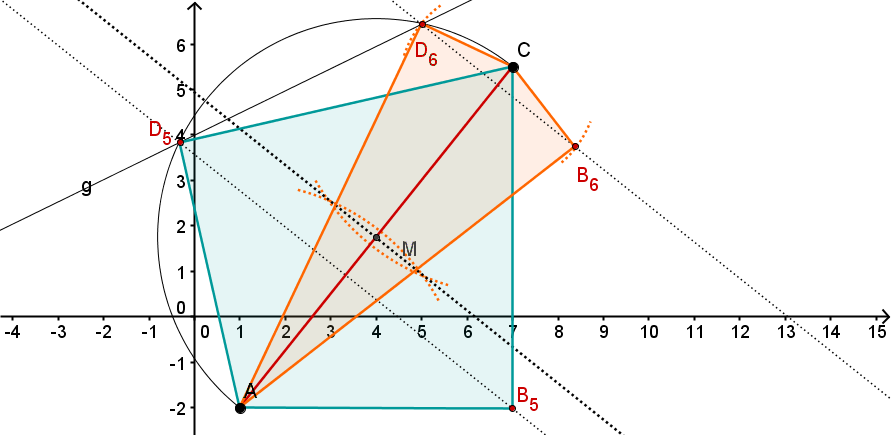
- 6
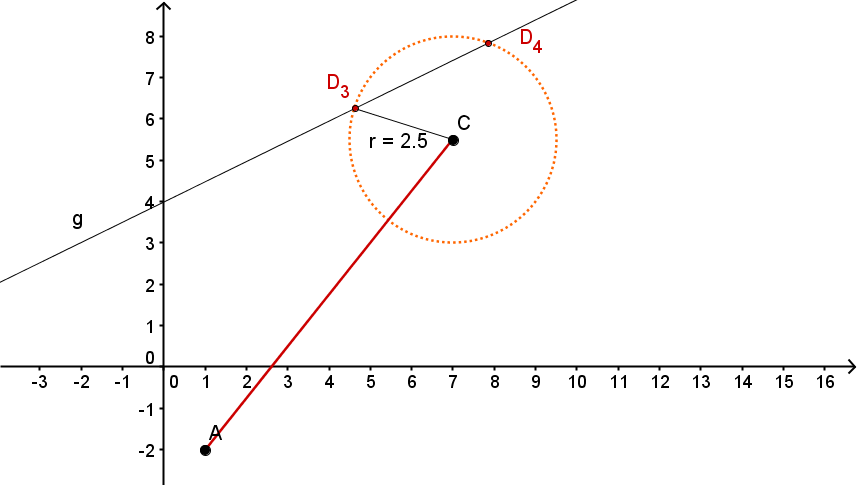
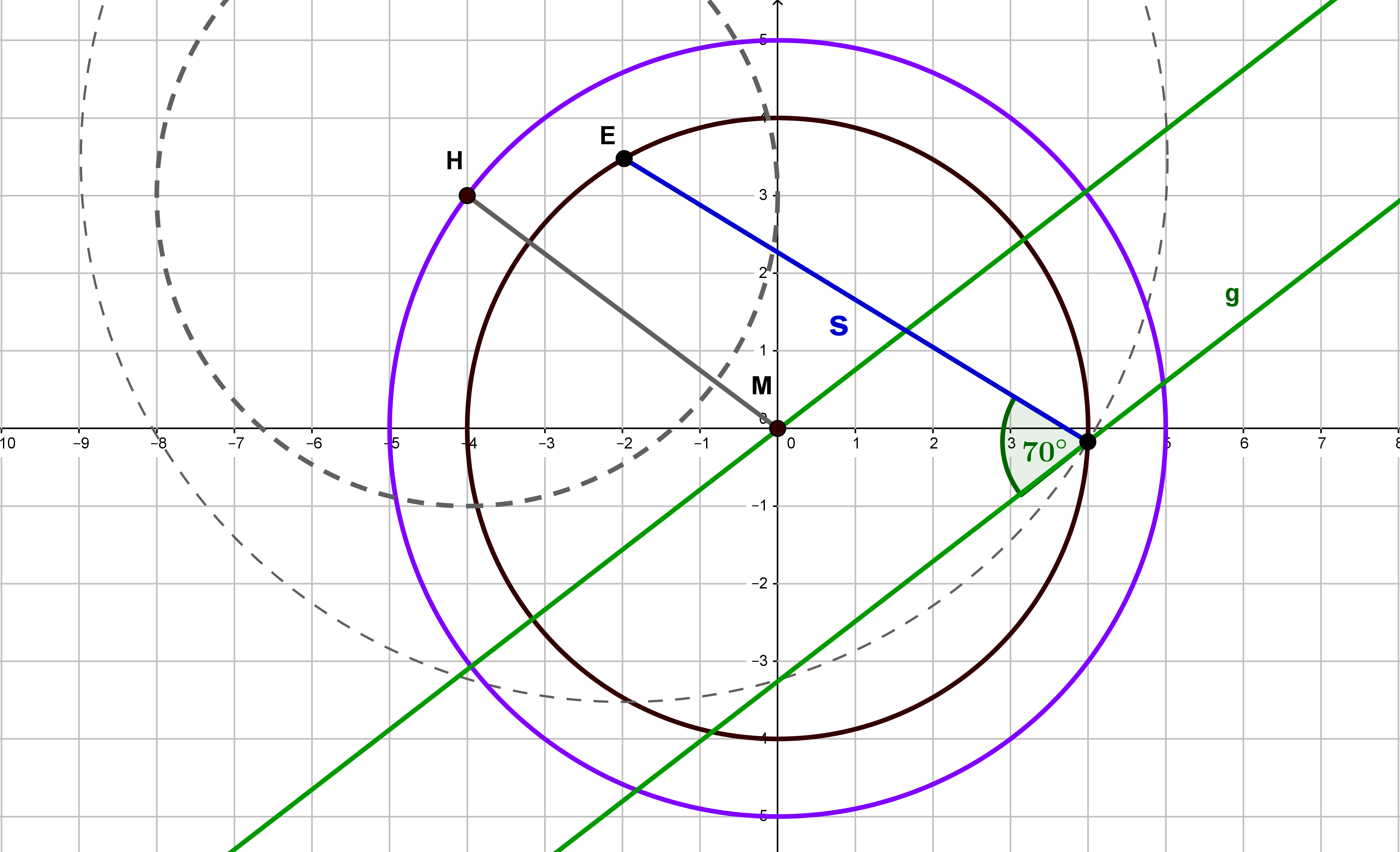
Gegeben sind die Punkte , und eine Schar von Drachenvierecken mit der Symmetrieachse .
Die Punkte liegen alle auf der Geraden .
(Es sind unendlich viele solcher und irgendwie sollen sie unterschieden werden – daher der Index : )
(Bewege den Regler und erhalte so verschiedene mögliche Punkte )
Konstruiere die Drachenvierecke und für die Werte bzw. x = - 2. (Unter verstehen wir die x-Koordinate des Punktes .)
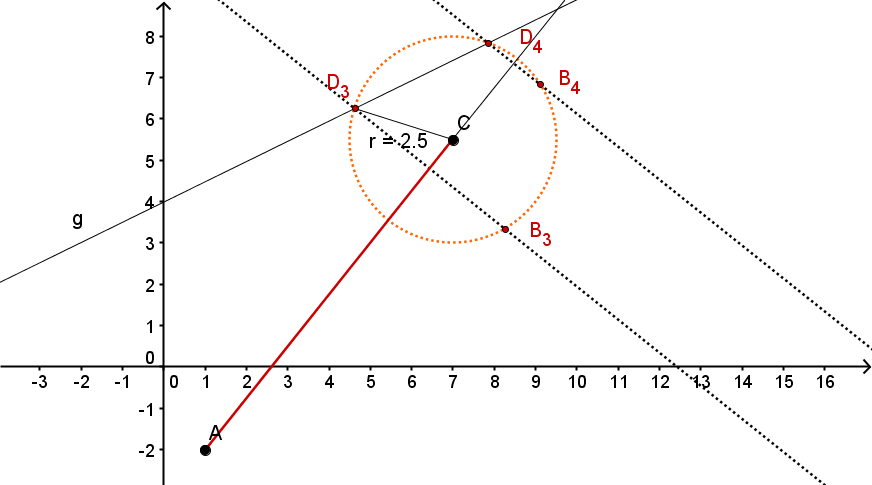
Konstruiere die Drachenvierecke und deren Seite das Maß hat.
Konstruiere die beiden Drachenvierecke und , bei denen das Maß des Winkels beträgt.
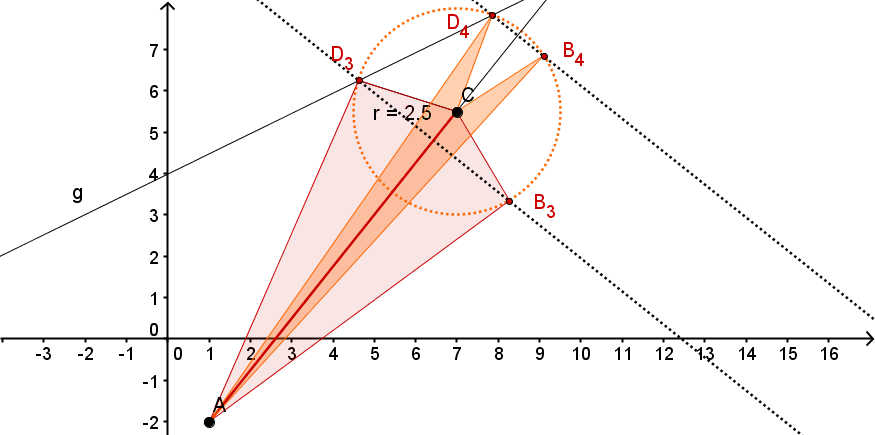
Unter den Drachen existiert auch eine Raute . Konstruiere sie.
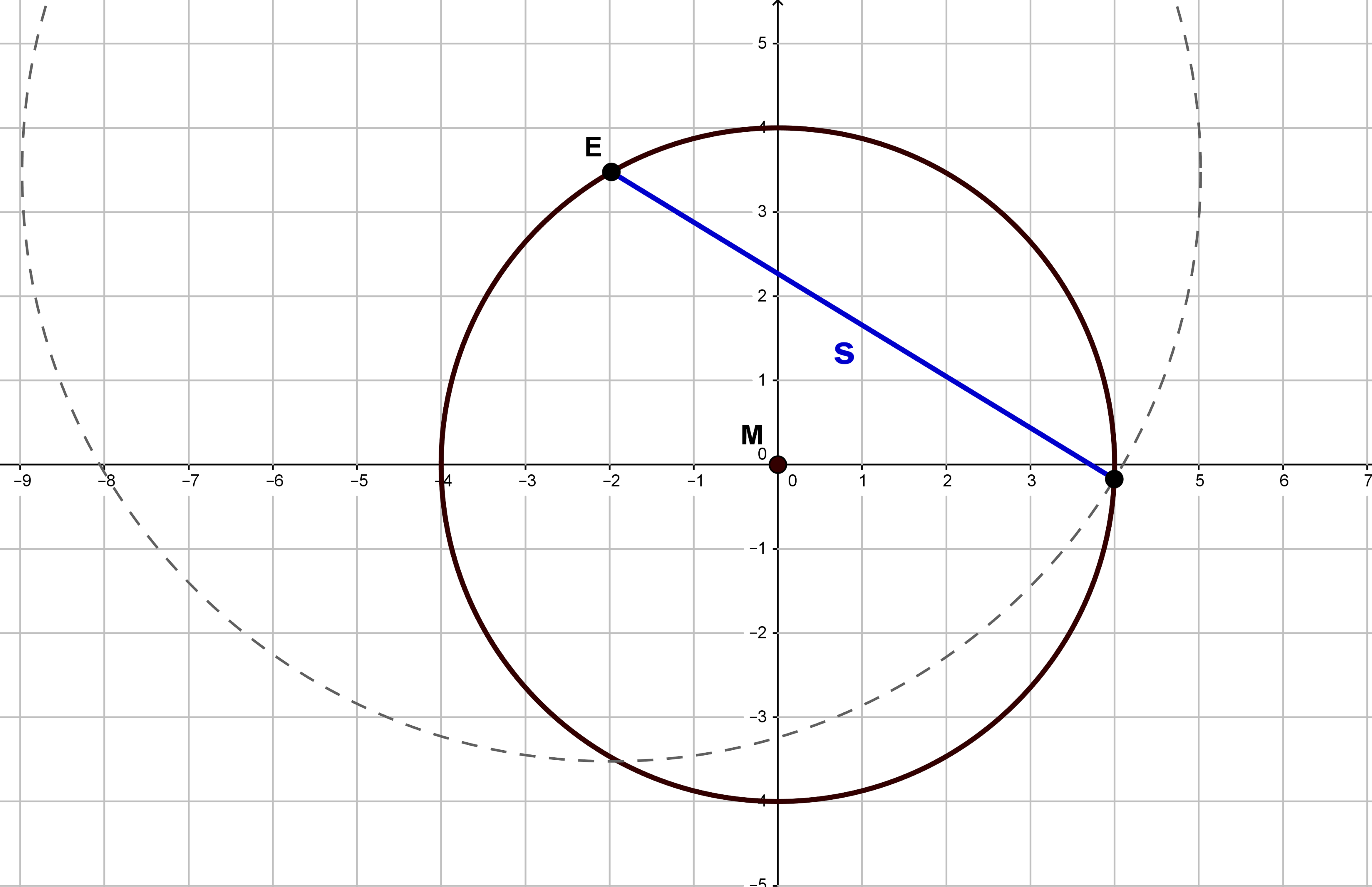
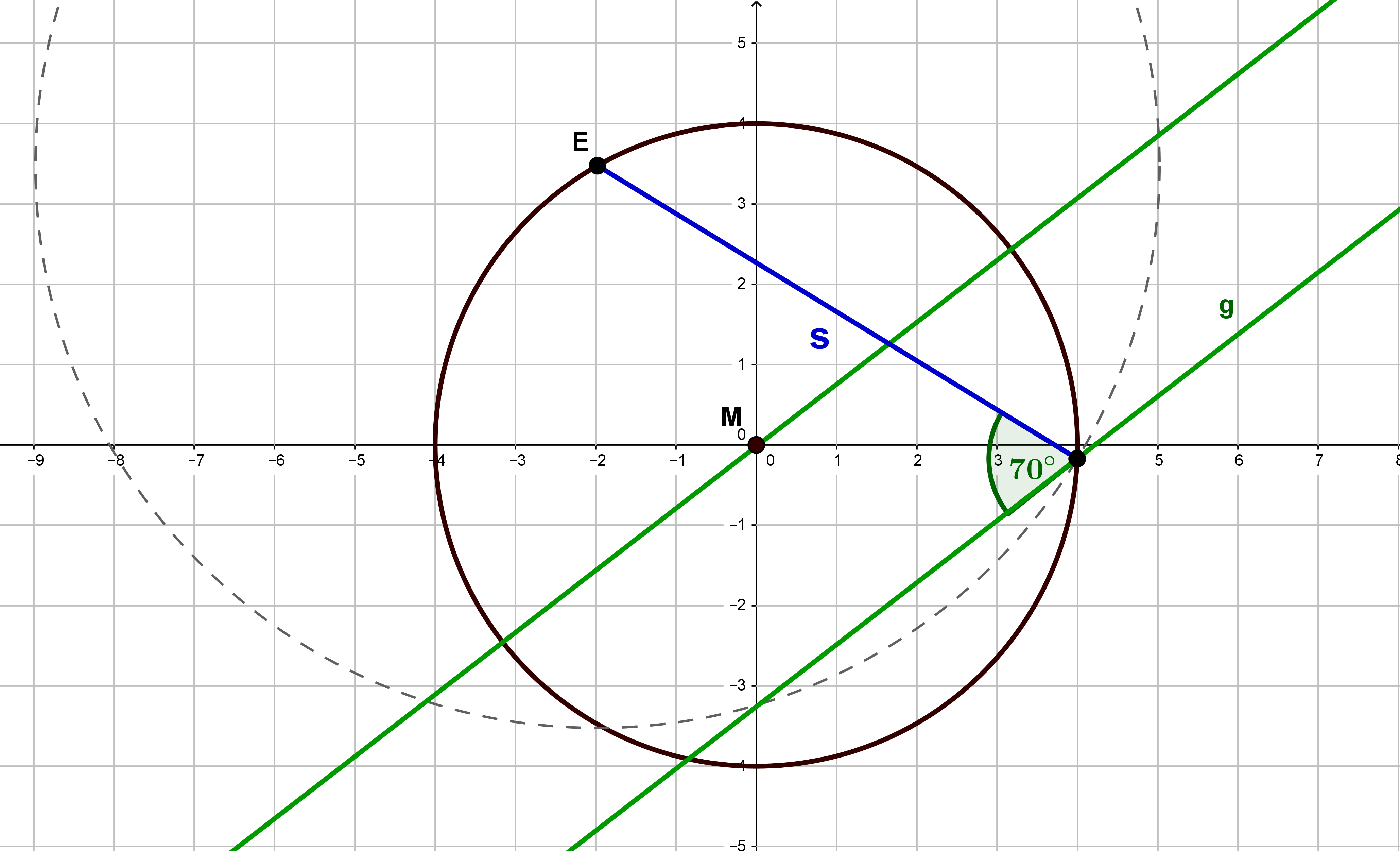
- 7
Führe die folgenden Konstruktionen durch und achte dabei darauf, dass sämtliche Konstruktionslinien deutlichen erkennbar sind. Schreibe die einzelnen Konstruktionsschritte auf.
Zeichne einen Kreis mit dem Radius und in diesen Kreis eine Sehne der Länge .
Konstruiere alle Sekanten durch , die mit einen Winkel von Grad einschließen und die Länge besitzen.
- 8
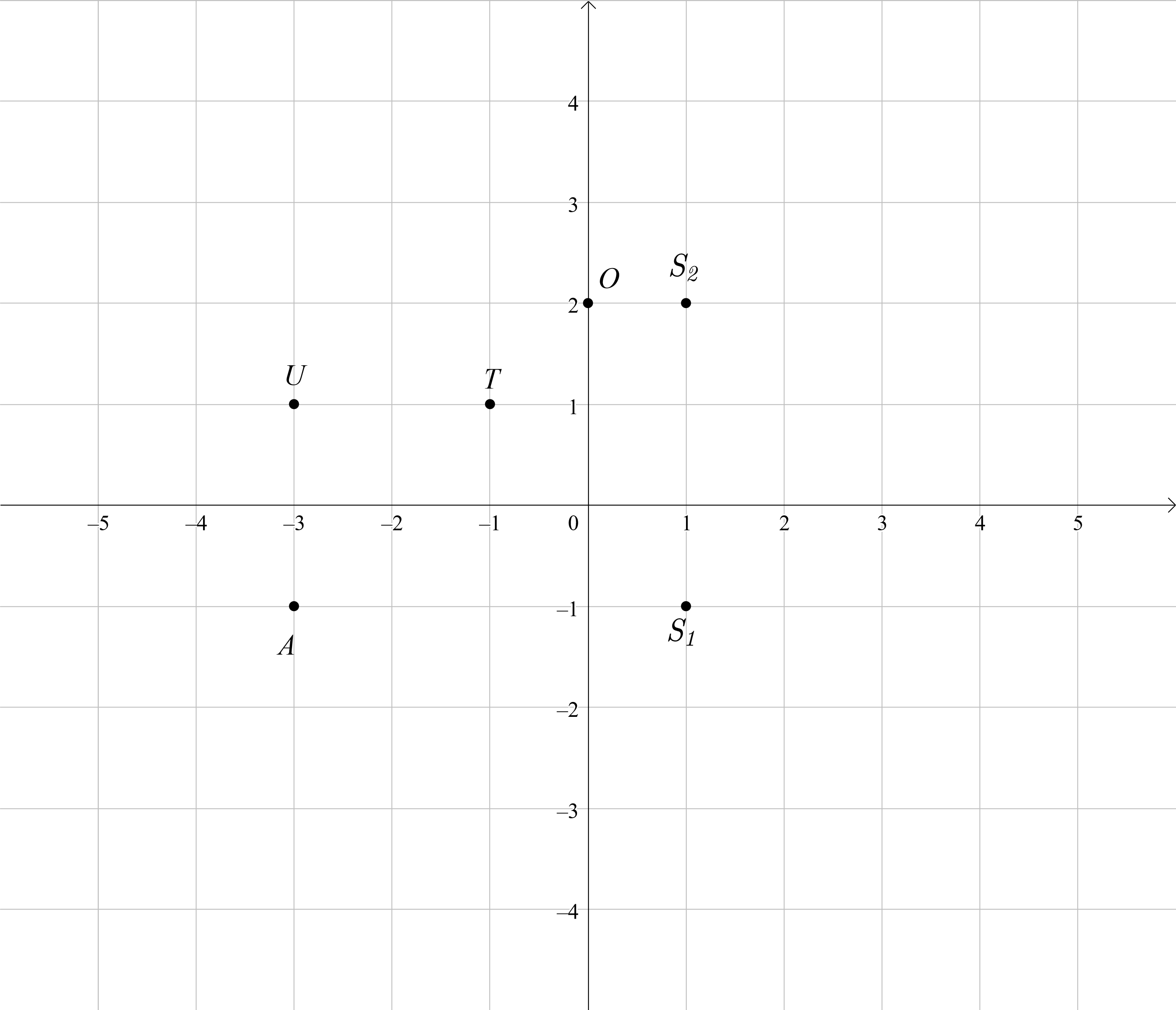
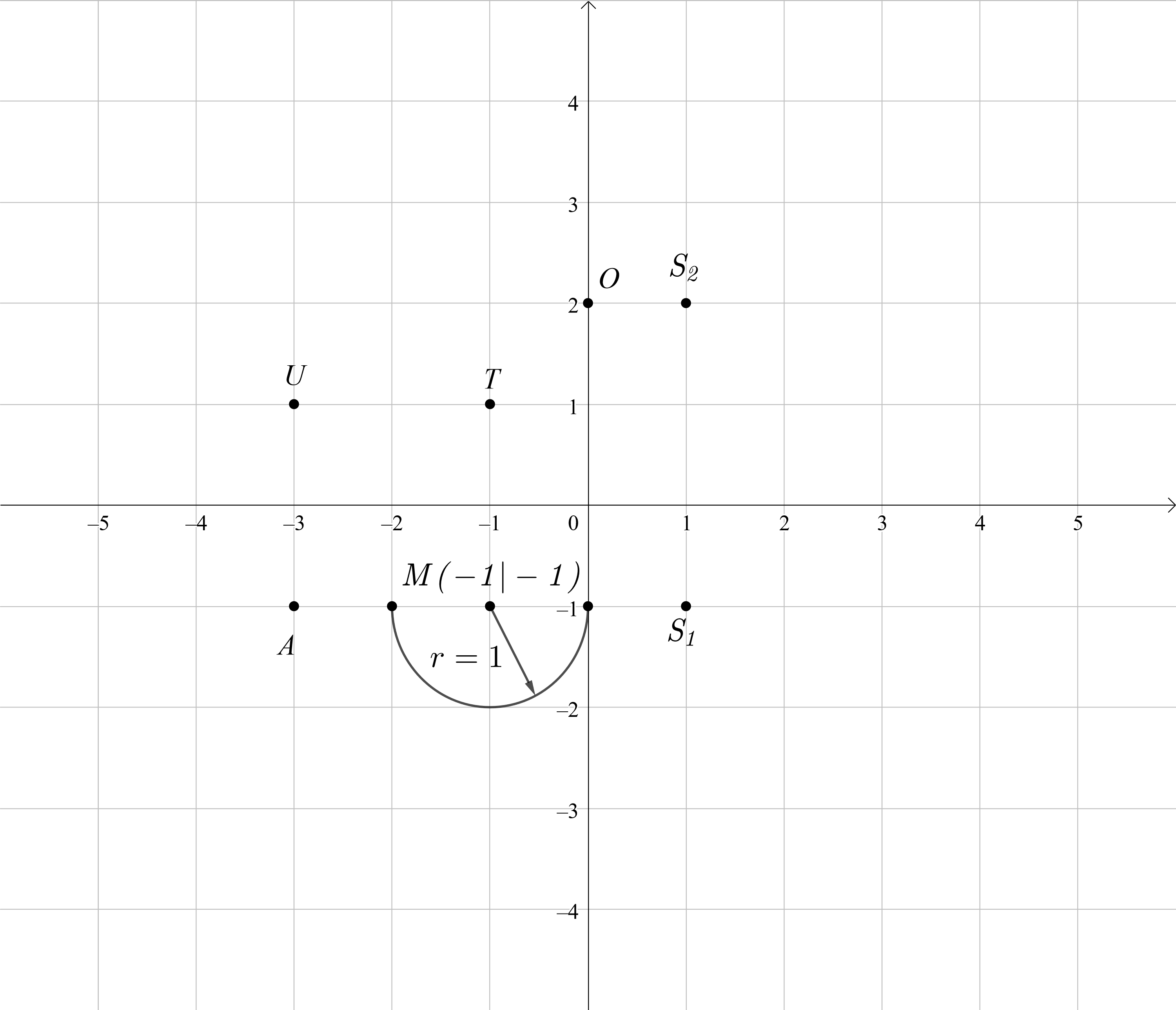
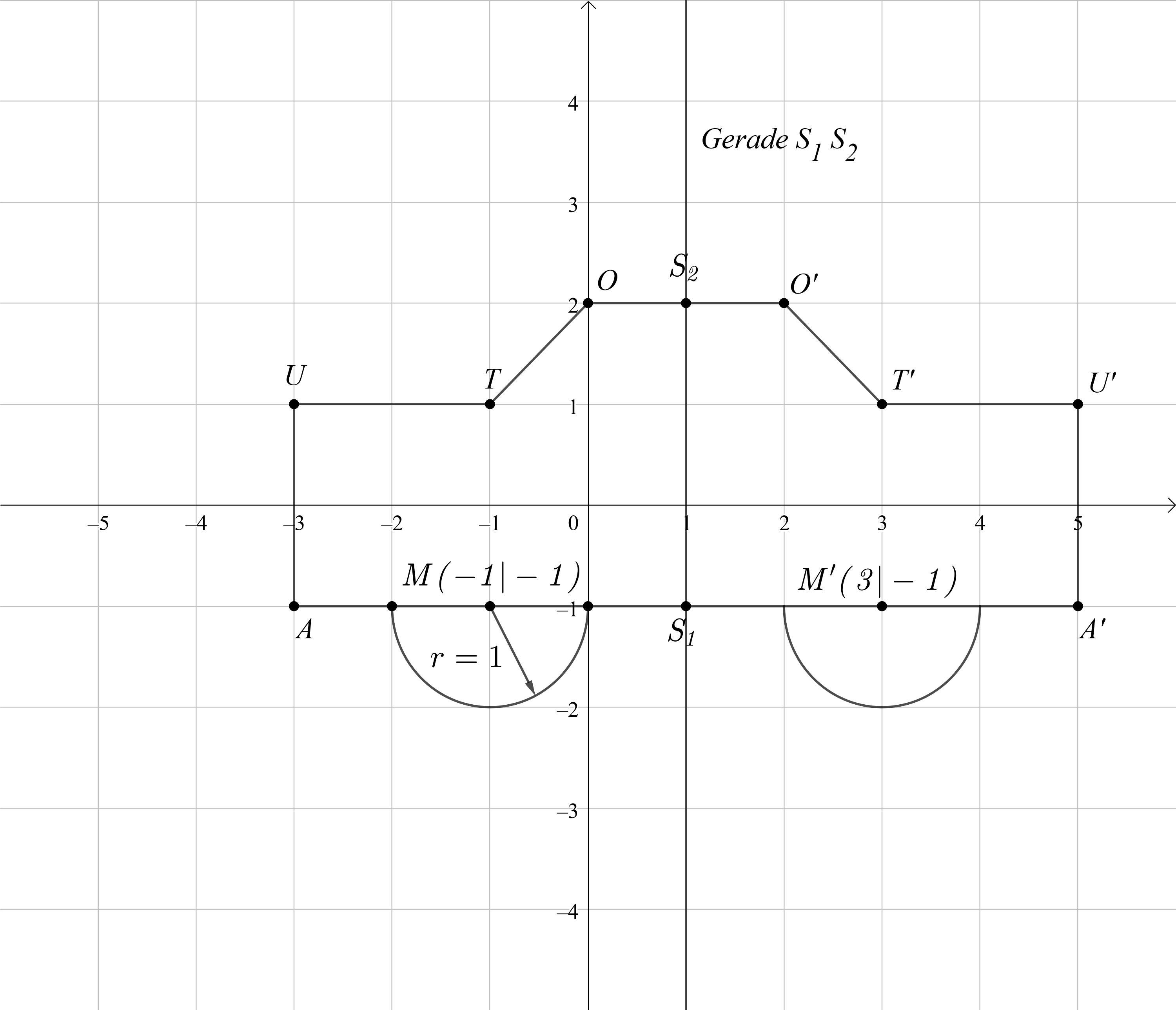
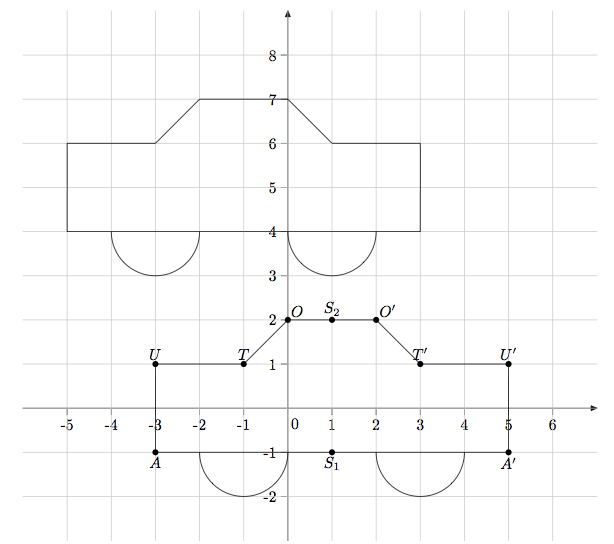
Zeichne die Punkte und in ein Koordinatensystem mit der Einheit .
Füge im Koordinatensystem einen nach oben geöffneten Halbkreis mit Mittelpunkt und Radius hinzu.
Spiegle die Punkte und den Halbkreis an der Gerade . Zeichne das Auto ein!
Verschiebe das Auto im Koordinatensystem um 2 Einheiten nach links und 5 Einheiten nach oben. Gib die Koordinaten der neu entstandenen Punkte an.
Formuliere eine Regel, wie man die Koordinaten der verschobenen Punkte berechnen kann.
Welche Koordinaten haben die Punkte, wenn das Auto um 13 Einheiten nach rechts und um 7 Einheiten nach unten verschoben wird?
- 9
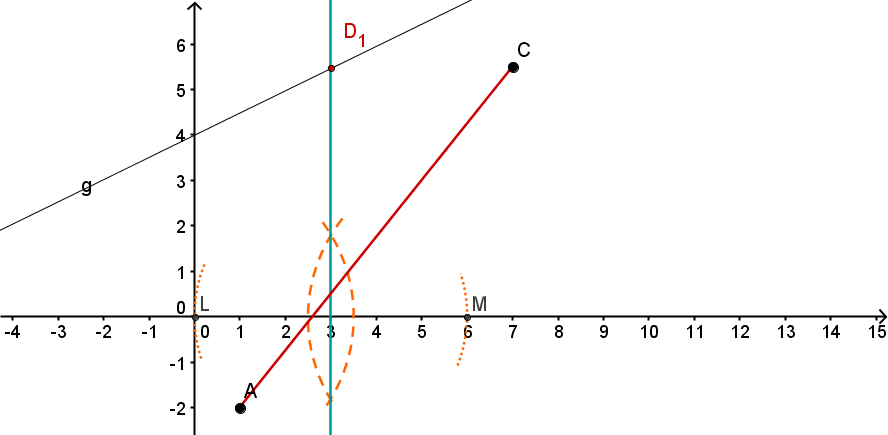
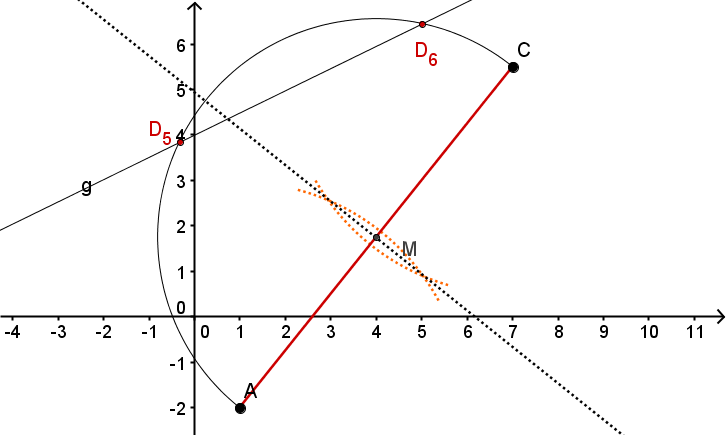
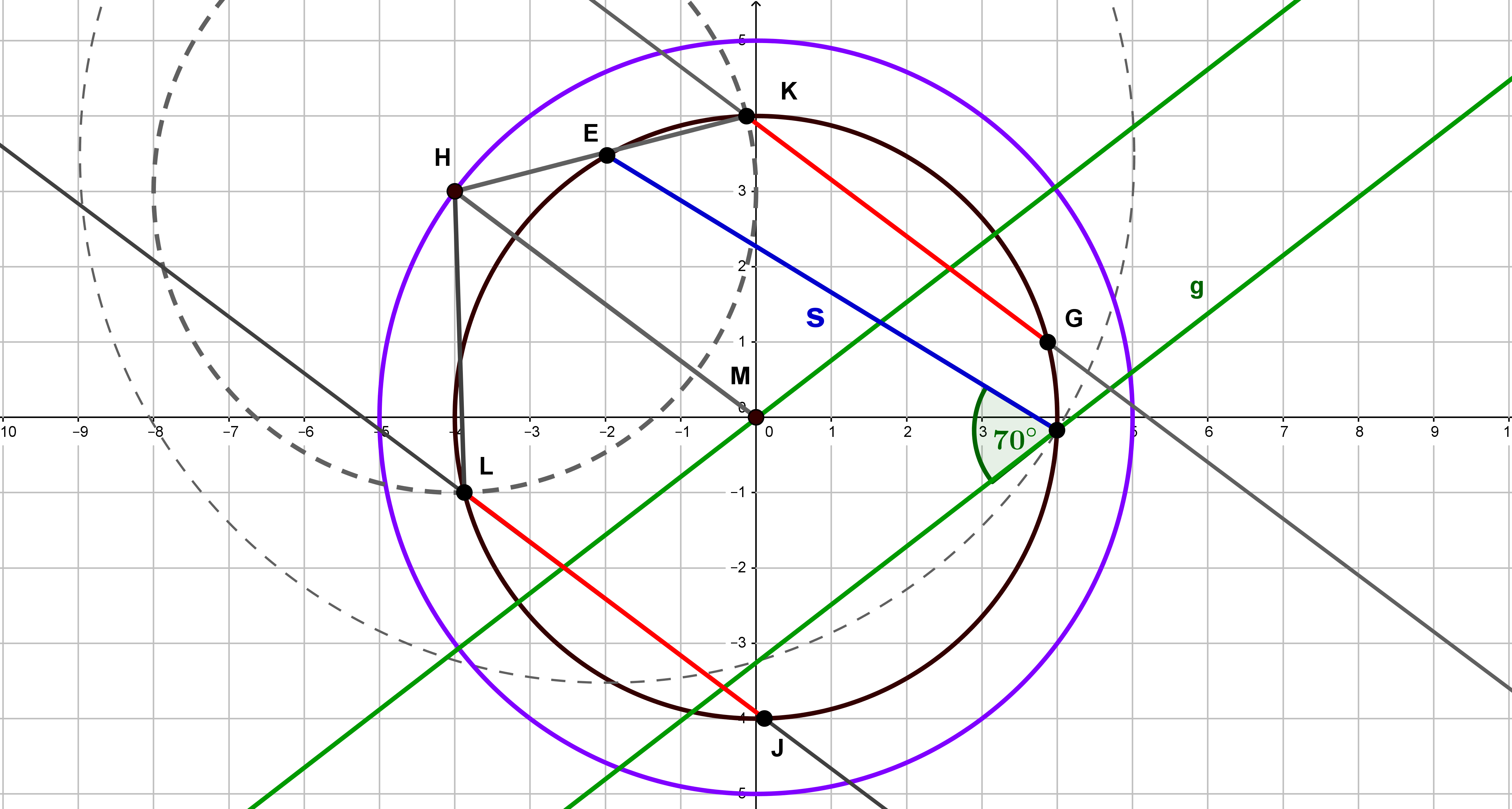
Gegeben ist eine Schar von (unendlich vielen) Vierecken .
Alle Punkte liegen auf der Geraden . Unter verstehen wir die -Koordinate eines Punktes . Unter seine -Koordinate.
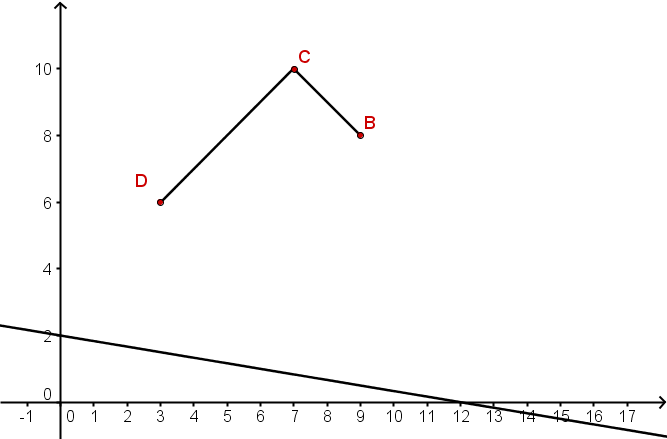
Konstruiere das Viereck , für . Was ist die y-Koordinate des Punktes ?
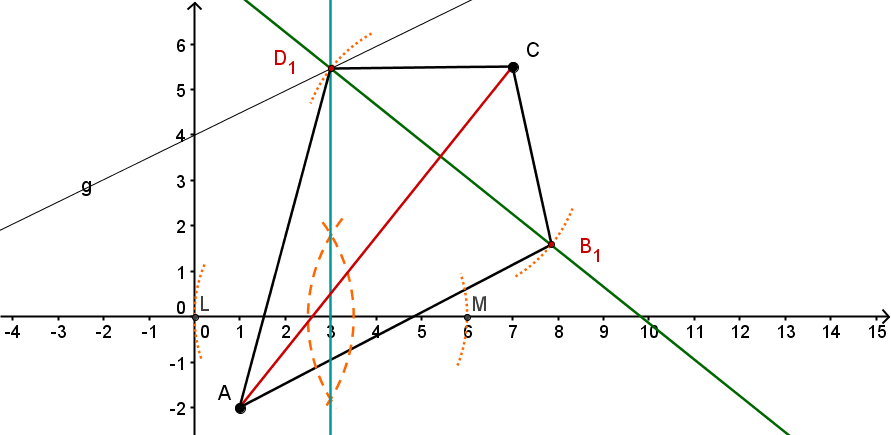
Unter den Vierecken gibt es genau zwei Trapeze, die wir und nennen. Konstruiere sie und gib die Koordinaten der Punkte und an.
Unter den Vierecken gibt es auch ein Drachenviereck . Konstruiere es und gib die Koordinaten des Punktes an.
Die Diagonalen des eben gezeichneten Drachenvierecks schneiden sich im Punkt . Berechne die Koordinaten vom Punkt .
Zeichne das Viereck , das man für erhält. Was ist an diesem Viereck anders als gewohnt?
Gibt es Werte von , für die man kein Viereck erhält? Bestimme sie durch Konstruktion.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?