Aufgaben zur Konstruktion von geometrischen Objekten

Gegeben sind die Punkte $A (1 | - 2)$ , $C (7 | 5,5)$ und eine Schar von Drachenvierecken $A B_{n} C D_{n}$ mit der Symmetrieachse $[A C]$ .

Die Punkte $D_{n} (x | y)$ liegen alle auf der Geraden $g$ .

(Es sind unendlich viele solcher $D_{n}$ und irgendwie sollen sie unterschieden werden – daher der Index $n$ : $D_{n}$ ⁣)

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/cqgnpdmb]

(Bewege den Regler und erhalte so verschiedene mögliche Punkte $D_{n}$ )

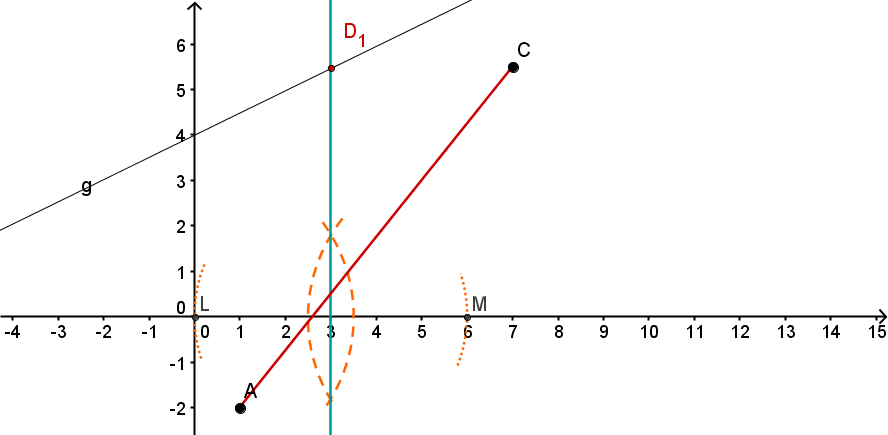
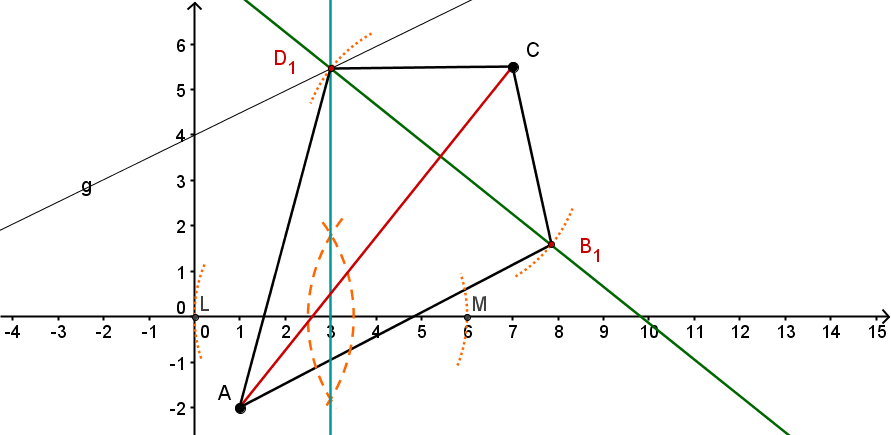
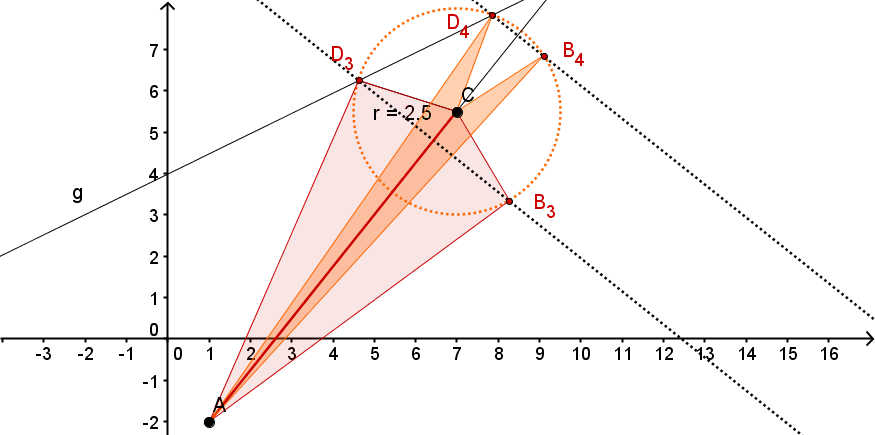
Konstruiere die Drachenvierecke $A B_{1} C D_{1}$ und $A B_{2} C D_{2}$ für die Werte $x = 3$ bzw. x = - 2. (Unter $x$ verstehen wir die x-Koordinate des Punktes $D_{n}$ .)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Mittelsenkrechte
Für x=3
Schritt 1
Konstruiere eine Senkrechte zur $x$ -Achse durch den Punkt $(3 | 0)$ . In der Zeichnung wird als eine Möglichkeit die Mittelsenkrechte der Strecke $[(0 | 0) (6 | 0)]$ konstruiert.
(Wie konstruiere ich eine Mittelsenkrechte?). $D_{1}$ ist der Schnittpunkt der Geraden $g$ mit dem Lot.
Schritt 2
Spiegle den Punkt $D_{1}$ an der Strecke $[AC]$ (Wie spiegle ich einen Punkt an einer Strecke?) und erhalte so $B_{1}$ . Verbinde dann die Punkte.
Für x=-2
Wiederhole die Schritte 1 und 2.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
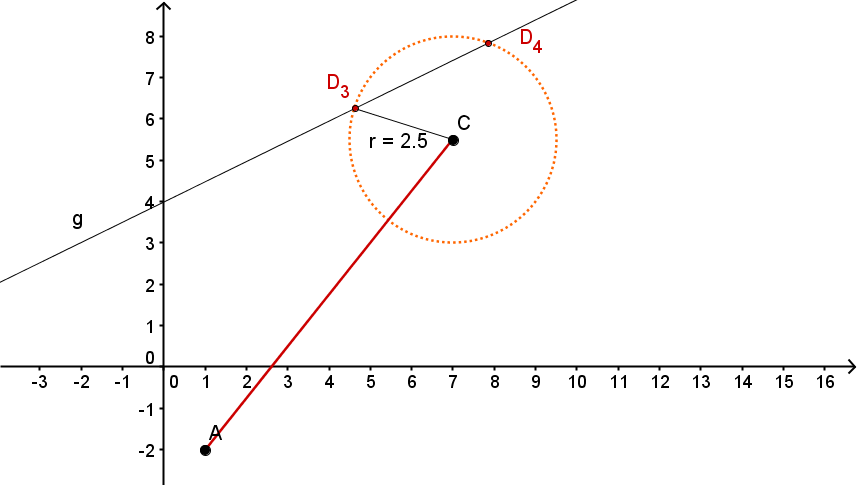
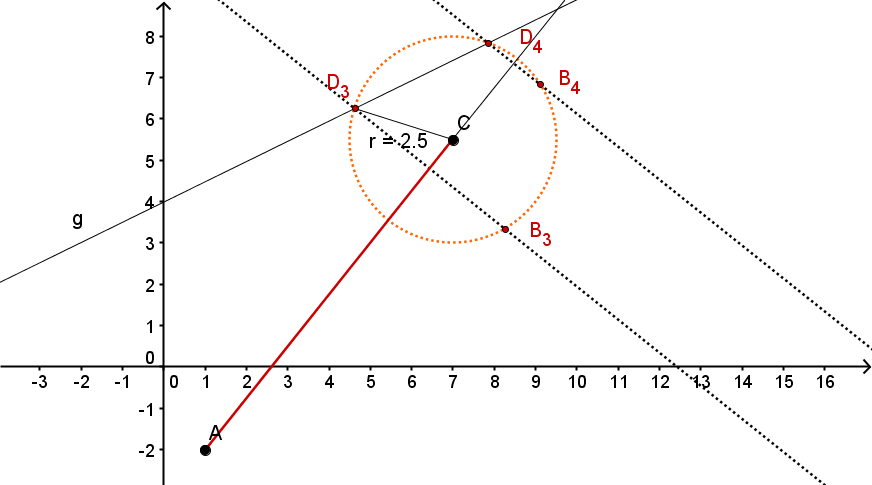
Konstruiere die Drachenvierecke $A B_{3} C D_{3}$ und $A B_{4} C D_{4}$ deren Seite $[C D]$ das Maß $2,5 cm$ hat.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Strecken/Geraden spiegeln
Schritt 1
Ziehe einen Kreis um $C$ mit Radius $r = 2,5$ . Erhalte $D_{3}$ und $D_{4}$ als Schnittpunkte des Kreises mit der Geraden $g$ .
Schritt 2
Lege eine Gerade durch die Strecke $[AC]$ . Spiegle $D_{3}$ und $D_{4}$ an der Gerade (Wie spiegle ich einen Punkt an einer Gerade/Strecke?) und erhalte so die Punkte $B_{3}$ und $B_{4}$ .
Schritt 3
Zeichne die Drachenvierecke $A B_{3} C D_{3}$ und $A B_{4} C D_{4}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
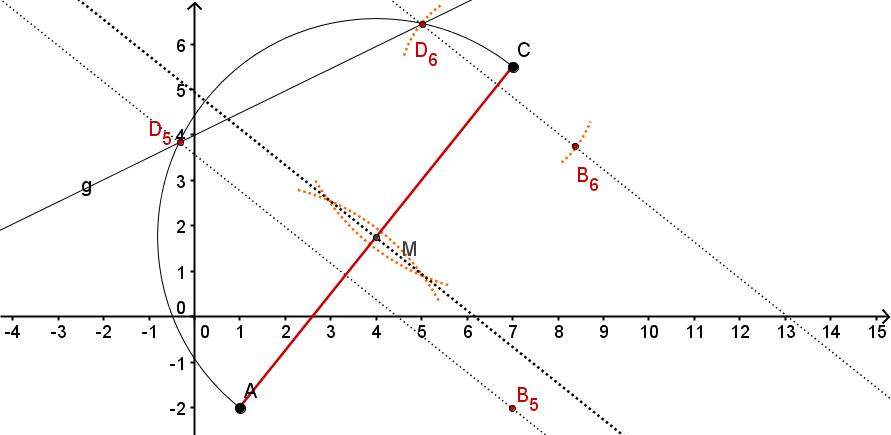
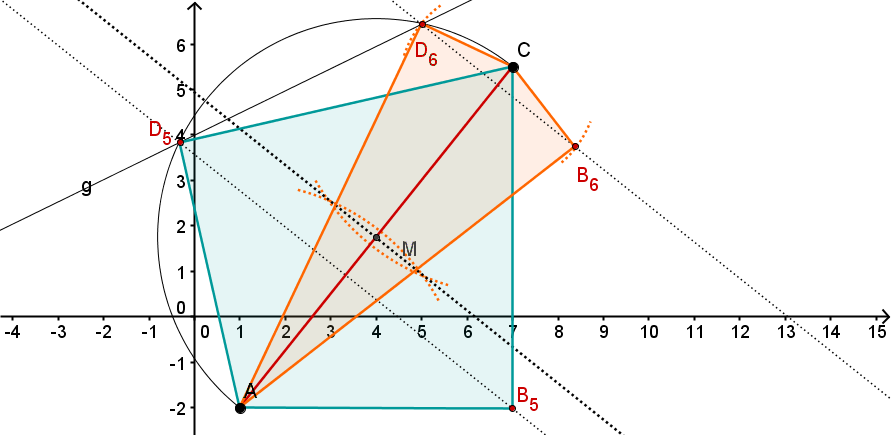
Konstruiere die beiden Drachenvierecke $A B_{5} C D_{5}$ und $A B_{6} C D_{6}$ , bei denen das Maß des Winkels $A D C$ $90^{\circ}$ beträgt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion eines Thaleskreises
Schritt 1
Konstruiere den Thaleskreis der Strecke $[AC]$ .(Wie konstruiere ich den Thaleskreis einer Strecke?). Dort liegen alle Punkte, die mit $B$ und $C$ einen rechten Winkel aufspannen. Erhalte $D_{5}$ und $D_{6}$ als Schnittpunkte des Kreises mit der Geraden.
Schritt 2
Spiegle die Punkte $D_{5}$ und $D_{6}$ an der Strecke $[AC]$ wie in Teilaufgabe a) und erhalte so die Punkte $B_{5}$ und $B_{6}$ .
Schritt 3
Verbinde die jeweiligen Punkte
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
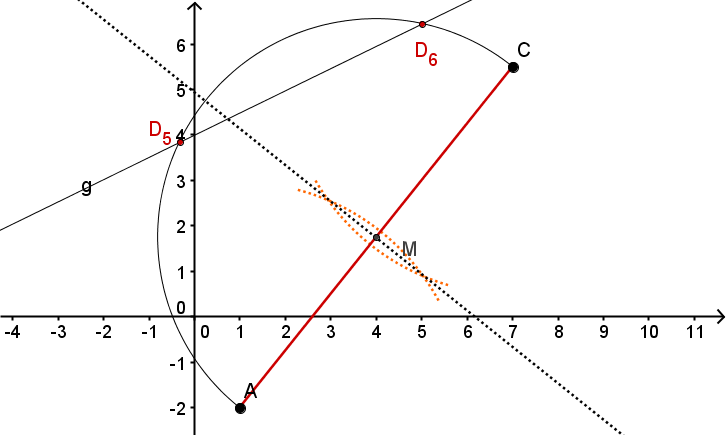
Unter den Drachen existiert auch eine Raute $A B_{7} C D_{7}$ . Konstruiere sie.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Bei einer Raute stehen die Diagonalen senkrecht aufeinander und halbieren sich.
Konstruiere daher die Mittelsenkrechte der Strecke $[A C]$ .
Der Schnittpunkt mit $g$ ist der Punkt $D_{7}$ .
$B_{7}$ erhältst du durch Spiegeln von $D_{7}$ an der Geraden durch $A$ und $C$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇