1 Kursübersicht

Malu befindet sich in einem Klassenraum und schaut sich genau um. Und bemerkt dabei an vielen verschiedenen Stellen Winkel.
Er findet Winkel an den Ecken der Tische, der Fenter, der Tafel, und sogar die Zeiger an der Uhr bilden einen Winkel.
In diesem Themenbereich erkundest du gemeinsam mit Malu den Klassenraum und beschäftigst dich dabei mit den folgenden Themen:
Was sind Winkel und wie entstehen sie?
Welche Arten von Winkeln gibt es?
Wie messen wir Winkel?
Wie zeichnen wir Winkel?
Wie Verhalten sich die Winkel in einem Dreieck?
Wir wünschen Dir viel Spaß beim Lernen!
2 Was sind Winkel und wie entstehen sie?
An der Wand des Klassenzimmers entdecken Malu und Bente eine Uhr. Den beiden fällt auf, dass alle Zeiger einen gemeinsamen Punkt haben, in dem sie sich treffen. Nur zeigen sie in verschiedene Richtungen. Die Zeiger der Uhr bilden jeweils Winkel:
Mit Winkeln (rot) können wir beschreiben, wie zwei Geraden, Strahlen oder Strecken auf einander treffen.

Mit Winkeln (rot) können wir beschreiben, wie zwei Geraden, Strahlen oder Strecken auf einander treffen.
Winkel können groß oder klein sein, je nachdem, wie weit sich die Linien oder Strahlen voneinander entfernen. Große Winkel bedeuten, dass die Linien weiter auseinander sind, während kleine Winkel bedeuten, dass sie näher beieinander liegen.

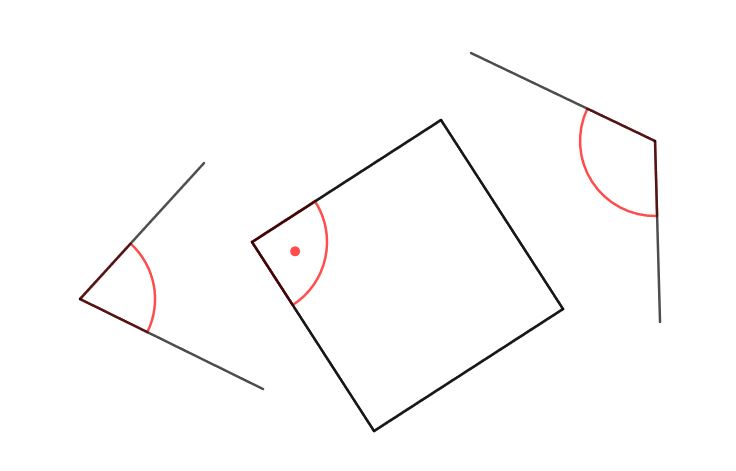
Bild 1: Drei Winkel (rot)

In diesem Bild siehst du einige Beispiele von Winkeln im Klassenraum
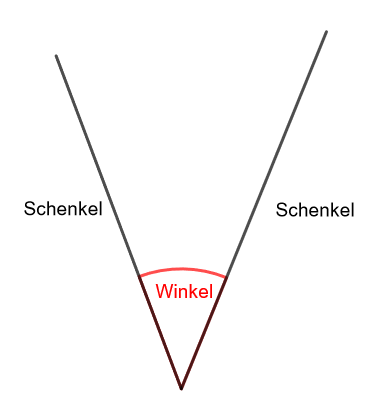
Was sind Schenkel?
Wie bereits erklärt, entsteht ein Winkel, wenn sich zwei Linien (also Geraden, Strahlen oder Strecken) treffen. Diese beiden Linien nennen wir Schenkel.
Was ist ein Scheitelpunkt?
Ein Scheitelpunkt ist der Punkt, in dem sich zwei Schenkel berühren.
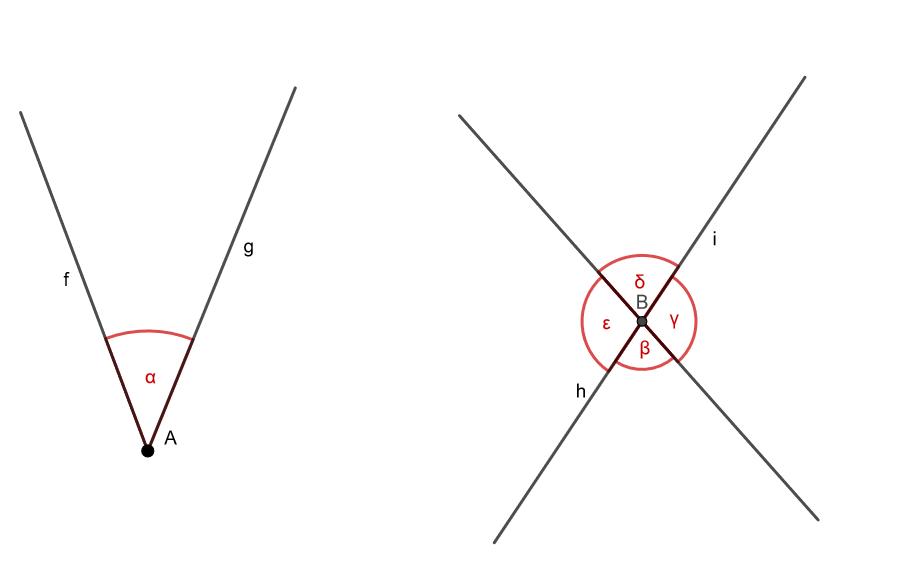
Die Punkte A und B sind Scheitelpunkte.
Warum Winkel?
Malu möchte versuchen die Lage zwischen zwei Geraden zu beschreiben, indem er Entfernungen zwischen den Schenkeln misst.
Er wählt einen Punkt auf dem ersten Schenkel (Punkt A), dann einen Punkt auf dem zweiten Schenkel (Punkt B). Anschließend Misst er die Entfernung zwischen den zwei Punkten.
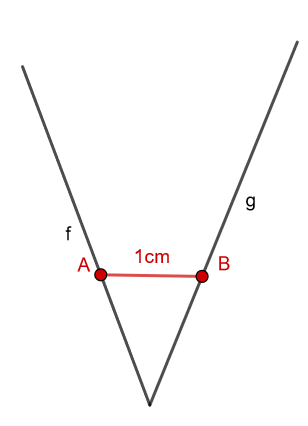
Malu misst die Entfernung zwischen A und B
Bente macht nun dasselbe.
Er misst die Entfernung der Punkte C und D.
Die beiden erkennen, dass die Entfernung unterschiedlich ist.
Die Entfernung der beiden Schenkel zueinander hängt also davon ab, wo man misst.
Deshalb können wir mit dieser Methode nicht gut beschreiben, wie die beiden Linien zu einander stehen. Genau deshalb benötigen wir Winkel.
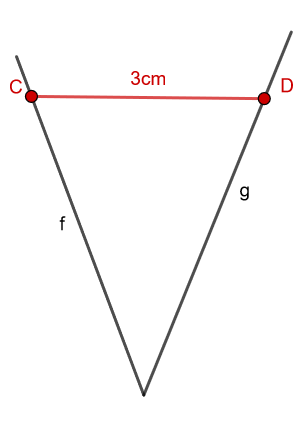
Bente misst die Entfernung zwischen C und D.
Die Größe eines Winkel hängt nicht davon ab, wo man misst.
Der Bogen für den Winkel α ist viel weiter oben gezeichnet als der Bogen für den Winkel β.
Dennoch sind beide Winkel gleich groß. Sie betragen 42°!
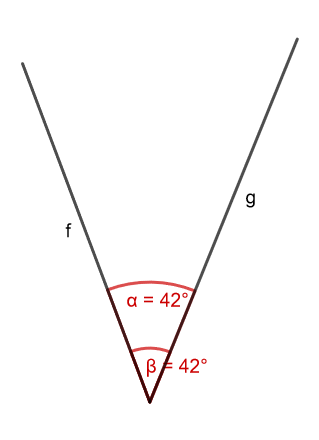
Wie du siehst, sind Winkel das richtige Maß, mit dem wir beschreiben können, wie zwei Geraden, Strahlen oder Strecken zueinander stehen.
Übungsaufgaben zum Erkennen vom Winkeln findest du hier.
3 Was sind Winkel und wie entstehen sie? - Teil 2
Winkel entstehen immer dann, wenn Geraden, Strahlen oder Strecken sich kreuzen oder berühren.
Wenn sie so zu einander stehen, dass sie sich nirgendwo schneiden oder berühren, dann entsteht auch kein Winkel.
Abbildung 1: Die beiden Strecken schneiden sich nicht. Deshalb entsteht hier kein Winkel.

Abbildung 1
Abbildung 2: Hier berühren sich die Geraden in einem Punkt und verlaufen in verschiedene Richtungen.
Wie du siehst, entstehen hier zwei Winkel. Du kannst diese auch als Innen- und Außenwinkel betrachten, mehr zu dem Thema folgt auf den nächsten Seiten.
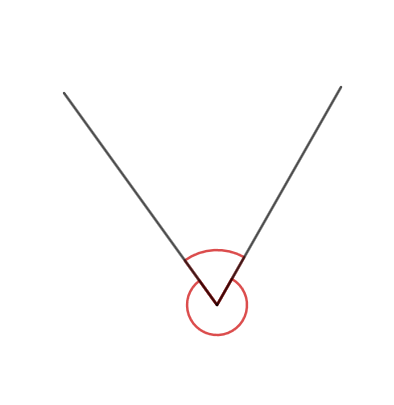
Abbildung 2:
Abbildung 3: Die beiden Strecken schneiden sich und es entstehen Winkel.
Hier kannst du etwas wichtiges beobachten:
Wenn sich zwei Geraden, Strahlen oder Strecken kreuzen, dann entstehen vier Winkel.
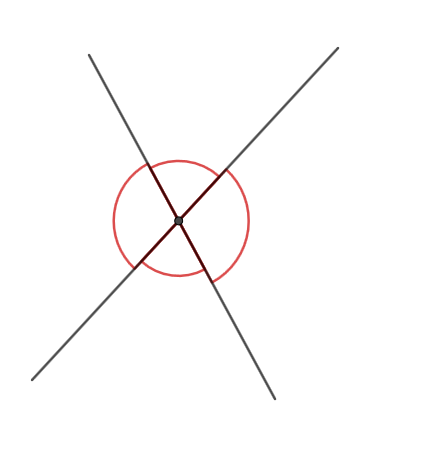
Abbildung 3
4 Welche Arten von Winkeln gibt es?
Du hast bereits gelernt, dass wir mit Winkeln beschreiben können, wie Strecken aufeinander treffen. Wir möchten uns nun anschauen, welche verschiedene Arten von Winkeln es gibt.
Nullwinkel
Ein Nullwinkel entsteht, wenn zwei Strecken genau aufeinanderliegen. Dieser beträgt 0° und ist nicht sichtbar.

Abbildung: Nullwinkel. Der Winkel beträgt 0° und ist nicht sichtbar, da die beiden Strecken auf einander liegen.
Spitze Winkel
Wenn zwei Gerade spitz auf einander zutreffen, dann heißt der Winkel spitzer Winkel. Spitze Winkel betragen zwischen 0° und 90°. Um dir leichter merken zu können, wie spitze Winkel aussehen, kannst du dir eine Bleistiftspitze vorstellen.
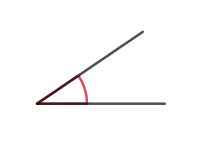
Abbildung: Spitzer Winkel. Spitze Winkel betragen zwischen 0° und 90°.
Rechte Winkel
Rechte Winkel sind in der Geometrie besonders wichtig und begegnen uns im Alltag am häufigsten. Egal ob die es die Ecken deines Heftes sind, deines Zimmers oder deines Schreibtisches. Rechte Winkel begegnen uns überall!
Für rechte Winkel gibt es eine besondere Beschriftung: Wir zeichnen in rechte Winkel einen Punkt ein.
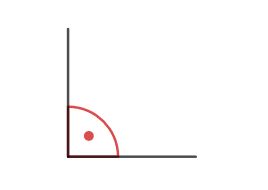
Abbildung: Rechter Winkel. Rechte Winkel betragen immer 90° und werden mit einem Punkt gekennzeichnet.
Stumpfe Winkel
Stumpfe Winkel sind Winkel, die zwischen rechten Winkeln und gestreckten Winkeln (siehe unten) liegen.
Ein stumpfer Winkel beträgt zwischen 90° und 180°. Um dir sein Aussehen zu merken, kannst du dir einen stumpfen Winkel als sehr stumpfe Bleistiftspitze vorstellen. Viele Hausdächer haben einen stumpfen Winkel, wobei es auch Dächer mit rechten oder mit spitzen Winkeln gibt.
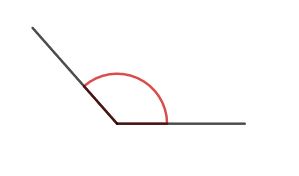
Abbildung: Stumper Winkel. Stumpfe Winkel betragen zwischen 90° und 180°.
Gestreckte Winkel
Gestreckte Winkel entstehen, wenn zwei Strecken auf einer Linie aufeinander treffen. Stelle dir einen Punkt vor, von dem aus zwei Strecken in entgegengesetze Richtungen verlaufen.
Gestreckte Winkel betragen immer 180°.
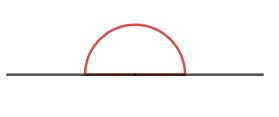
Abbildung: Gestreckter Winkel. Gestreckte Winkel betragen immer 180°.
Überstumpfe Winkel
Überstumpfe Winkel sind Winkel, die zwischen 180° und 360° betragen. Du kannst sie dir als Gegenstück zu spitzen, rechten und stumpfen Winkel vorstellen: Immer wenn zwei Strecken aufeinander treffen und ein spitzer, rechter oder stumpfer Winkel entsteht, so entsteht auf der gegenüberliegenden Seite ein überstumpfer Winkel.

Abbildung: Überstumpfer Winkel. Überstumpfe Winkel betragen zwischen 180° und 360°.
Vollwinkel
Wie bei den überstumpfen Winkeln bereits angedeutet kannst du Winkel immer an zwei Seiten messen (siehe Abschnitt Innen- und Außenwinkel//todo:Verlinkung). Vollwinkel sind das Gegenstück zu Nullwinkeln. Ein Vollwinkel entsteht, genau wie beim Nullwinkel, wenn zwei Strecken aufeinander liegen. Nur messen wir nun statt von innen (0°) von Außen und erhalten eine komplette Umrundung (360°).
Abbildung: Vollwinkel. Vollwinkel betragen immer 360°.
Übersicht aller Winkelarten
Bezeichnung | Größe des Winkels | Bemerkung |
|---|---|---|
Nullwinkel | α = 0° | Beide Geraden liegen aufeinander, Winkel nicht sichtbar |
spitzer Winkel | 0° < α < 90° | Merke: Bleistiftspitze |
rechter Winkel | α = 90° | Merke: Ecken deines Hefts |
stumpfer Winkel | 90° < α < 180° | Merke: Sehr stumpfe Spitze oder Dach eines Hauses |
gestreckter Winkel | α = 180° | Beide Geraden zeigen in die entgegengesetzte Richtung |
überstumpfer Winkel | 180° < α < 360° | Gegenstück zu spitzen, rechten und stumpfen Winkeln |
Vollwinkel | α = 360° | Beide Geraden liegen aufeinander, Gegenstück zum Nullwinkel |
In dem folgenden Geogebra-Applet kannst du dir nochmal anschauen, wie alle Winkel aussehen. Klicke jeweils auf den Winkel, den du betrachten möchtest.
In diesem Abschnitt hast du sieben Arten von Winkeln kennengelernt. Von klein nach groß:
Nullwinkel, spitzer Winkel, rechter Winkel, stumpfer Winkel, überstumpfer Winkel und Vollwinkel.
Aufgaben zu Arten von Winkeln findest du hier.
5 Welche Arten von Winkeln gibt es? - Teil 2
Wir möchten uns auf dieser Seite den Unterschied zwischen Innen- und Außenwinkeln anschauen.
Wenn man von einem Innenwinkel spricht, dann meint man damit den Winkel innerhalb eines Körpers oder einer Fläche.
Zu jedem Innenwinkel lässt sich auch ein Außenwinkel finden. Der Außenwinkel ist der Winkel, der sich ergibt, wenn man stattdessen außen, also außerhalb des Körpers oder Fläche misst.
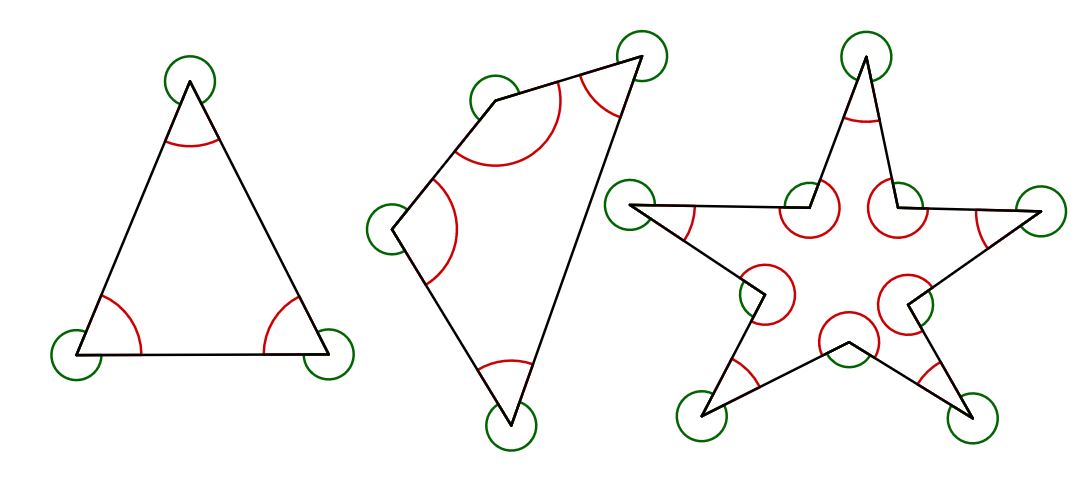
Abbildung: Drei verschiedene Flächen. Alle Innenwinkel sind rot und alle Außenwinkel sind grün.
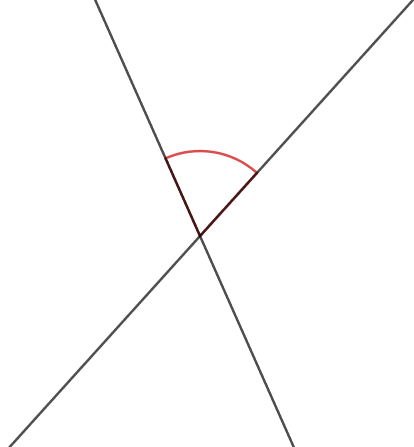
Abbildung: Spitzer Winkel an zwei Geraden
Handelt es sich bei dem obigen Winkel um einen Innenwinkel oder einen Außenwinkel? Das können wir nicht sagen, da es sich hier um zwei Geraden handelt. Um Innenwinkel und Außenwinkel bestimmten zu können, brauchen wie eine geschlossene Fläche oder eine Figur. Ansonsten können wir nicht sagen ob ein Winkel ein Innenwinkel oder ein Außenwinkel ist.
Wann immer du einen Innenwinkel (rot) und seinen Außenwinkel (grün) zusammenaddierst, dann ist die Summe 360°.
Übungsaufgaben zu Innenwinkeln und Außenwinkeln findest du hier.
6 Wie messen wir Winkel?
Das Geodreieck
Bevor dir Malu zeigt, wie du mit dem Geodreieck Winkel misst, haben wir für dich eine kurze Einführung zum Geodreieck vorbeitet: (WIP)
Nun hast du sehen, wie du das Geodreieck benutzen kannst. Das wichtigste hier nochmal in Kürze:
Auf dem Geodreieck gibt es zwei Zahlenbögen, die von 0° bis 180° und von 180° bis 0° gehen
Öffnet sich der Winkel von rechts, wird die Gradzahl auf dem Geodreieck von rechts nach links größer
Öffnet sich der Winkel von links, wird die Gradzahl auf dem Geodreieck von links nach rechts größer
Winkel mit dem Geodreieck messen
Jetzt zeigt dir Malu nochmal in Kürze, wie genau du Schritt für Schritt einen Winkel messen kannst. Schaue aufmerksam zu:
Winkel, die über 180° groß sind
Wie dir vermutlich schon aufgefallen ist, kannst du mit dem Geo-Dreieck nur bis 180°
messen. Wir möchten dir nun zwei Methoden zeigen, wie du Winkel messen kannst,
die über 180° sind.
1. Methode: 180° + Rest
Jeden Winkel, der 180° groß ist, kannst du aufteilen. Genauer gesagt beachtest du den Winkel bis 180° nicht und misst nur den restlichen Teilwinkel aus, der von 180° bis zum eigentlichen Winkel geht. Diese Methode zeigt dir Malu hier:
2. Methode: Differenz von 360°
Wie du in einem vorherigen Kapitel gelernt hast, entspricht eine komplette Umdrehung ("ein Mal im Kreis drehen") 360°. Das können wir uns zu Nutze machen:
Jeder Winkel α, egal wie klein oder groß α ist, hat einen gegenüberliegenden Winkel β.
Dabei gilt immer: α + β = 360°.
Malu wird dir nun genauer zeigen, was damit gemeint ist:
Übungsaufgaben zum Messen von Winkel findest du hier.
Aufgaben zum Messen von Winkeln findest du hier.
7 Wie zeichnen wir Winkel?
In dem folgenden Geogebra Applet zeigt die Malu Schritt für Schritt, wie du einen Winkel zeichnest.
8 Wie beschriften wir Winkel?
In der folgenden Grafik siehst du beispielhaft, wie man in einer Figur alles richtig beschriftet.
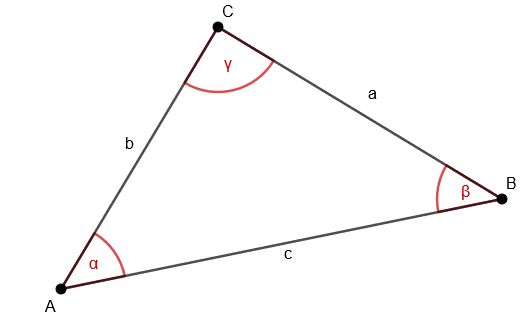
Abbildung: Vollständig beschriftetes Dreieck
In der Geometrie gelten die folgenden Regeln:
Punkte bezeichnen wir mit lateinischen Großbuchstaben (hier: A, B, C)
Seiten bezeichnen wir mit lateinischen Kleinbuchstaben (hier: a, b, c)
Zuletzt das, worum es in diesem Kurs eigentlich geht:
Winkel bezeichnen wir mit griechischen Kleinbuchstaben (hier: α, β, γ)
Unser deutsches Alphabet stammt vom lateinischen Alphabet ab. Im deutschen Alphabet haben wir zusätzlich G, Y, Z, und die Umlaute Ä, Ö, Ü. Diese Buchstaben gibt im lateinischen Alphabet nämlich nicht.
Immer dann, wenn du auf Groß- oder Kleinbuchstaben aus unserem "normalen" Alphabet triffst (z.B. a, B, N oder k), dann nennen sich diese Buchstaben lateinische Buchstaben.
Das griechische Alphabet
Keine Sorge, du musst nicht das gesamte griechische Alphabet auswendig lernen, das wäre viel zu viel. In der Schule reichen für die Geometrie meistens die ersten fünf griechischen Buchstaben aus.
Und das sind sie:
Deutscher (lateinischer) Kleinbuchstabe | Griechischer Kleinbuchstabe | Griechischer Großbuchstabe | Ausgeschrieben |
|---|---|---|---|
a | α | Α | alpha (das "ph" spricht man wie "f" aus, also "alfa") |
b | β | Β | beta |
c | γ | Γ | gamma |
d | δ | Δ | delta |
e | ε | Ε | epsilon |
Aufgaben zur Beschriftung von Winkeln findest du hier.
9 Wie Verhalten sich die Winkel in einem Dreieck?
Dreiecke haben eine interessante Eigenschaft. Egal, wie das Dreieck aussieht.
Messen wir die drei Innenwinkel und summieren sie auf, so erhalten wir immer 180°!
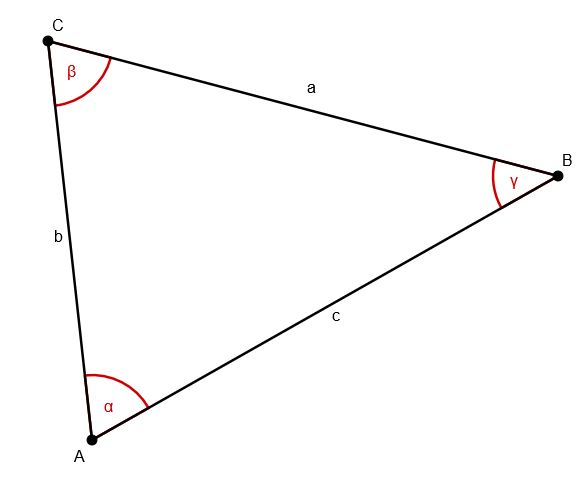
Merke: für jedes Dreieck gilt α+β+γ=180°.
In dem folgenden Applet kannst du den Punkt C verschieben. Wie du siehst ändern sich zwar die Größen der einzelnen Winkel. Jedoch bleibt die Winkelsumme stets gleich!
Übungsaufgaben zur Winkelsumme von Dreiecken findest du hier.
