Wir wollen in diesem Artikel verstehen wie wir zur Flächeninhaltsformel für das Rechteck kommen.
Zur Erinnerung die Formel lautet:
wobei a und b die Längen zweier anliegenden Seiten im Rechteck sind.
Dafür müssen wir zuerst einmal klären, was der Flächeninhalt überhaupt sein soll. Betrachten wir mal folgende Flächen:
Der Flächeninhalt einer geometrischen Form ist die Menge an "Farbe" die in die Form hineinpasst. Nun ist es oftmals gar nicht so leicht zu sagen, wie viel Farbe in eine Form hineinpasst; vor allem wenn diese eine komplizierte Gestalt hat.
Was wir nun also zuerst brauchen ist ein "Messeinheit", sodass wir die Farbe die wir in die Form gießen vorher abmessen können. In der Mathematik hat man sich darauf geeinigt als "Messeinheit" (kleine) Einheitsquadrate zu nehmen. Einheitsquadrate sind Quadrate, bei denen die Seitenlänge 1 ist. Denn mit diesen kann man besonders gut viele wichtige Flächen unterteilen. Wenn wir also zum Beispiel wissen, dass in eine vorgegebene Form 5 Einheitsquadrate passen, dann können wir sagen: In diese Form passt 5 mal so viel Farbe wie in ein Einheitsquadrat. Auf diese Weise können wir dann Flächen miteinander vergleichen. Passt in eine erste Form mehr Einheitsquadrate als in eine zweite, so muss der Flächeninhalt der ersten größer sein, als die der zweiten. Wir verschieben also sozusagen die Frage, wie groß der Flächeninhalt eines Objekts ist hinzu der Frage, wie viele Einheitsquadrate in dieses hineinpassen. Wir wollen nach diesen Überlegungen folgenden Merksatz festhalten:
Wie kann man nun herausfinden, wie viele Einheitsquadrate in ein vorgegebenes Rechteck passen?
Betrachten wir dazu folgendes Rechteck und seine Unterteilung in Einheitsquadrate:
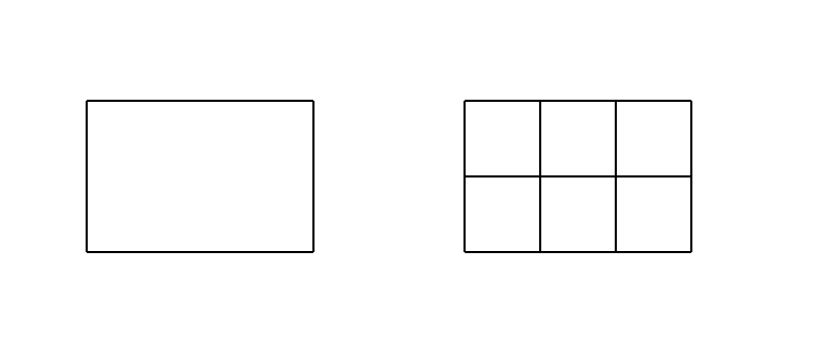
In das obige Bild gehen nun genau 6 Einheitsquadrate hinein, indem wir sie einfach zählen und zwar auf folgende Weise: Zuerst zählen wir die unterste Reihe (von links nach rechts)
