1 Ritter Theo
Ritter Theo wollte die Aussicht von einer alten Burg genießen. Da der Eingang verschlossen war, entdeckte er eine Leiter, die an die Mauer gelehnt war. Um sicher die 8 Meter hohe Mauer zu erklimmen, musste er wissen, ob die Leiter lang genug war. Die Leiter war 2 Meter von der Mauer entfernt aufgestellt.
Wie lang muss die Leiter mindestens sein, damit Theo sicher die Mauer erreichen kann?
8.25 m
8.5 m
10.72 m
7.3 m
2 Der schiefe Turm
Einst gab es einen schiefen Turm in der Stadt Geometrika, und alle Bürger waren besorgt, dass er umfallen könnte. Der Turm stand schräg, sodass der Winkel zum Boden
𝛼=49 Grad betrug. Ein Ingenieur namens Alex wurde gerufen, um die Länge des Seils zu berechnen, das benötigt wird, um den Turm zu stabilisieren. Das Seil sollte vom oberen Punkt des Turms bis zu einem sicheren Punkt auf dem Boden gespannt werden, und die Höhe des Turms betrug a=1,6 m.
Wie lang muss das Seil b sein, um den Turm zu stabilisieren?
1,39 m
1,35 m
1,50 m
1,05 cm
3 Die Hängebrücke
In einem kleinen Dorf in den Bergen plante der Architekt Leo den Bau einer Hängebrücke über einen Fluss. Die Brücke sollte zwei Uferpunkte A und B verbinden, wobei der Punkt A auf dem rechten Ufer und der Punkt B auf einem Felsen am linken Ufer lag. Leo wusste, dass die Höhe des Felsens (die senkrechte Entfernung) a=5,1 m und die horizontale Entfernung zwischen den beiden Uferpunkten b=7,5 m betrug. Um die Gesamtlänge der Brücke zu berechnen, musste Leo die Länge des schrägen Seils c ermitteln, das zwischen den Punkten A und B gespannt werden sollte.
9,07 m
8,92 m
9,22 m
9,12 m
4 Der mutige Vogel
Ein kleiner Vogel namens Pico wollte zu einem hohen Baum fliegen, um dort sein Nest zu bauen. Um dorthin zu gelangen, flog Pico von einem Punkt C am Boden auf den Ast eines Baumes (Punkt B), der a = 3,1 m über dem Boden lag. Der Baum bildete einen Winkel von β=54 Grad
mit dem Boden. Pico wollte wissen, wie weit der Ast (Punkt A) vom Stamm entfernt ist, um zu wissen, wie weit er fliegen musste.
Wie weit muss Pico fliegen, um von Punkt B direkt auf den Ast A zu gelangen?
5,27 m
4,20 m
4,50 m
3,80 m
5 Die Bergverbindung
Die Geschichte von der Hängebrücke in den Bergen
In einem abgelegenen Bergdorf gab es drei wichtige Punkte: das Dorf A, den Aussichtspunkt B und die Spitze des Berges C. Die Dorfbewohner wollten eine Hängebrücke zwischen dem Aussichtspunkt B und der Bergspitze C bauen, um die Reisezeit zu verkürzen. Die Länge der Strecke von A nach C betrug b=1,7 m, und die Winkel betrugen α=81 Grad
und γ=60 Grad.
Nun wollten die Dorfbewohner wissen, wie lang die Brücke a sein müsste, um die Punkte B und C direkt zu verbinden.
a = 2,67 m
2,25 m
2,10 m
1,95 m
6 Der Dreiecksteich
In einem kleinen Dorf gab es einen mysteriösen Teich in der Form eines Dreiecks. Die Dorfbewohner nannten ihn den „Dreiecksteich“, weil er von drei großen Steinen an den Punkten A, B und C umgeben war. Um den Teich zu vermessen, legte der Geometer Leonore ein Dreieck über den Teich, wobei die Seitenlängen des Dreiecks a=4,6 m und b=4,9 m betrugen. Der Winkel
𝛾 zwischen diesen beiden Seiten betrug 80 ∘ . Leonore wollte nun wissen, wie lang die Seite c war, die die Punkte A und B direkt verband.
6,11 m
6,07 m
6,19 m
6,43 m
7 Die Architektenprüfung
In einem weit entfernten Land lebte eine talentierte junge Architektin namens Sofia. Um ihre Fähigkeiten unter Beweis zu stellen, musste sie eine schwierige Prüfung bestehen. Ihr wurde ein gleichschenkliges Dreieck ABC gezeigt, bei dem die Seiten und jeweils 11 m lang waren. Der Winkel betrug und .
Sofia soll den Winkel berechnen.
14,12°
9,45°
62,12°
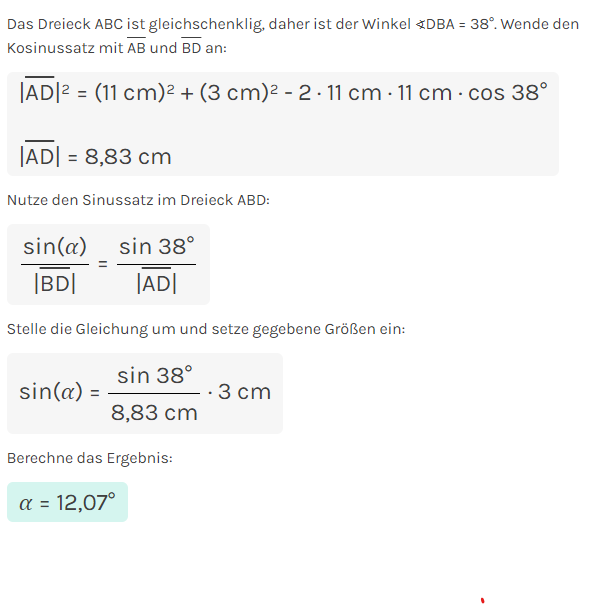
8 Die geheime Schatzkarte
In einem alten Schloss entdeckte der junge Entdecker Max eine alte Schatzkarte. Auf der Karte war ein gleichschenkliges Dreieck ABC abgebildet, das den Weg zu einem verborgenen Schatz zeigte. Die Seiten |AB| und |AC| waren jeweils 11 cm lang, und der Winkel ∢ACB betrug 38°.
Um die genaue Position des Schatzes zu bestimmen, muss Max den Winkel 𝛼 berechnen.
9,41°
12,21°
7,34°
8,28°