Stackautomat

Die Sprache $L = \{\mathsf a^n\mathsf b^n ~|~ n \in\mathbb N \}$ ist nicht regulär, daher kannst du sie nicht mit einem endlichen Automaten erkennen. Aber du kannst sie wunderbar einfach mit einem Stackautomaten erkennen.

Ein Stackautomat ist quasi ein endlicher Automat, der aber zusätzlich mit einem Stack ausgerüstet ist.

Ein Stack ist ein Speicher, der wie ein Stapel funktioniert: Wenn du Daten hinzufügst, legst du sie oben auf den Stapel, wenn du Daten wieder entnimmst, dann immer nur vom oberen Ende des Stapels. Du kannst nicht auf weiter unten im Stapel liegende Daten zugreifen.

Funktionsweise

Stell dir vor, du bist der Stackautomat: Während du ein Wort $\mathsf a^n\mathsf b^n$ der Sprache $L$ einliest, packst du jedes gelesene a auf den Stack. Sobald ein b kommt, schaltest du um und entfernst von nun an für jedes gelesene b ein a vom Stack. Wenn du das gesamte Wort eingelesen hast und der Stack leer ist, hast du das Wort erkannt (Ablauf wie im folgenden Bild).

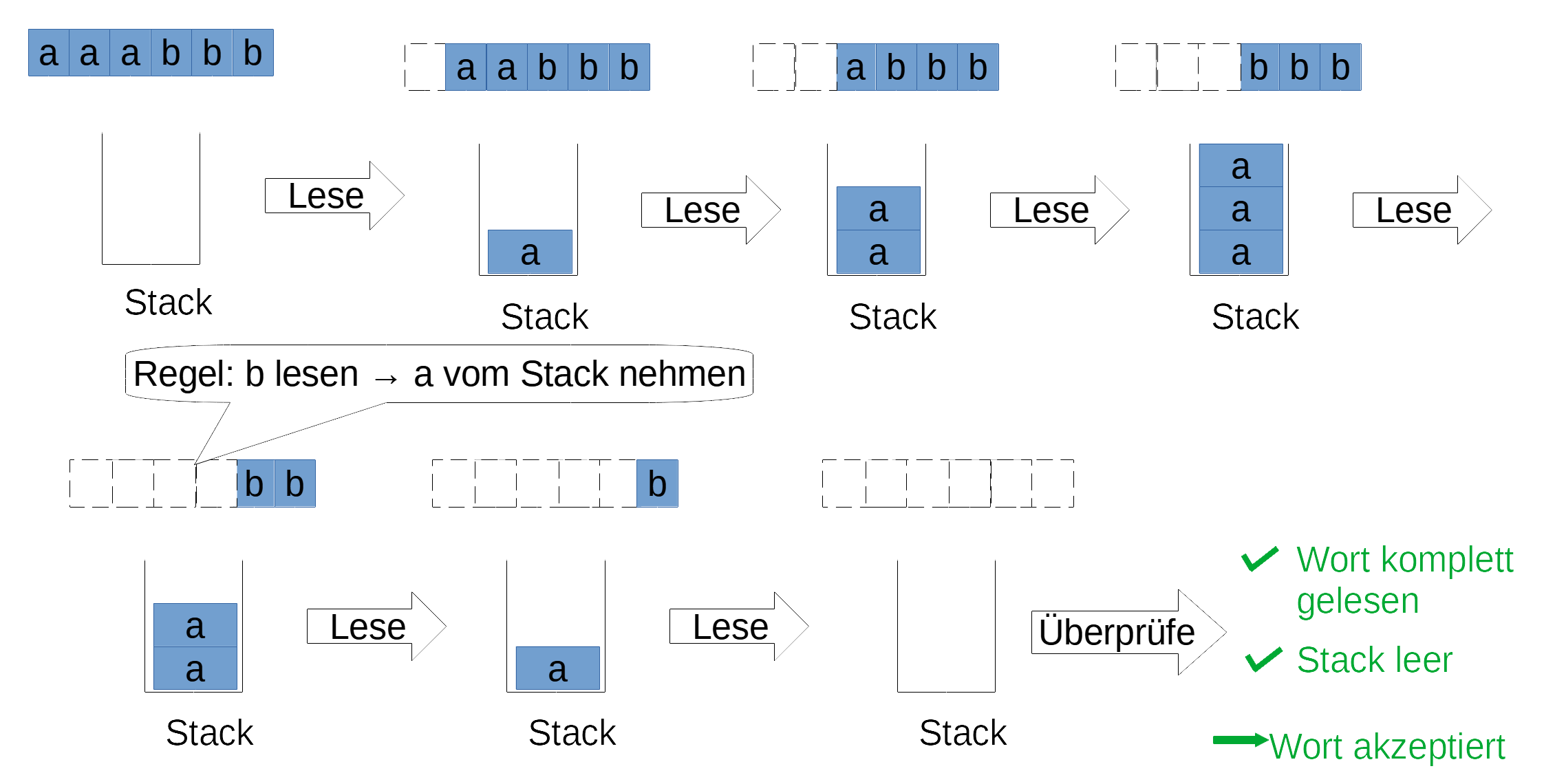
In allen anderen Fällen weist du das Wort zurück. Etwa wenn du schon dabei bist, a's vom Stack zu entfernen, und du liest erneut ein a. Oder wenn du das gesamte Wort eingelesen hast und der Stack anschließend nicht leer ist. Oder wenn der Stack leer ist, aber du noch nicht das ganze Wort eingelesen hast (siehe folgendes Bild).

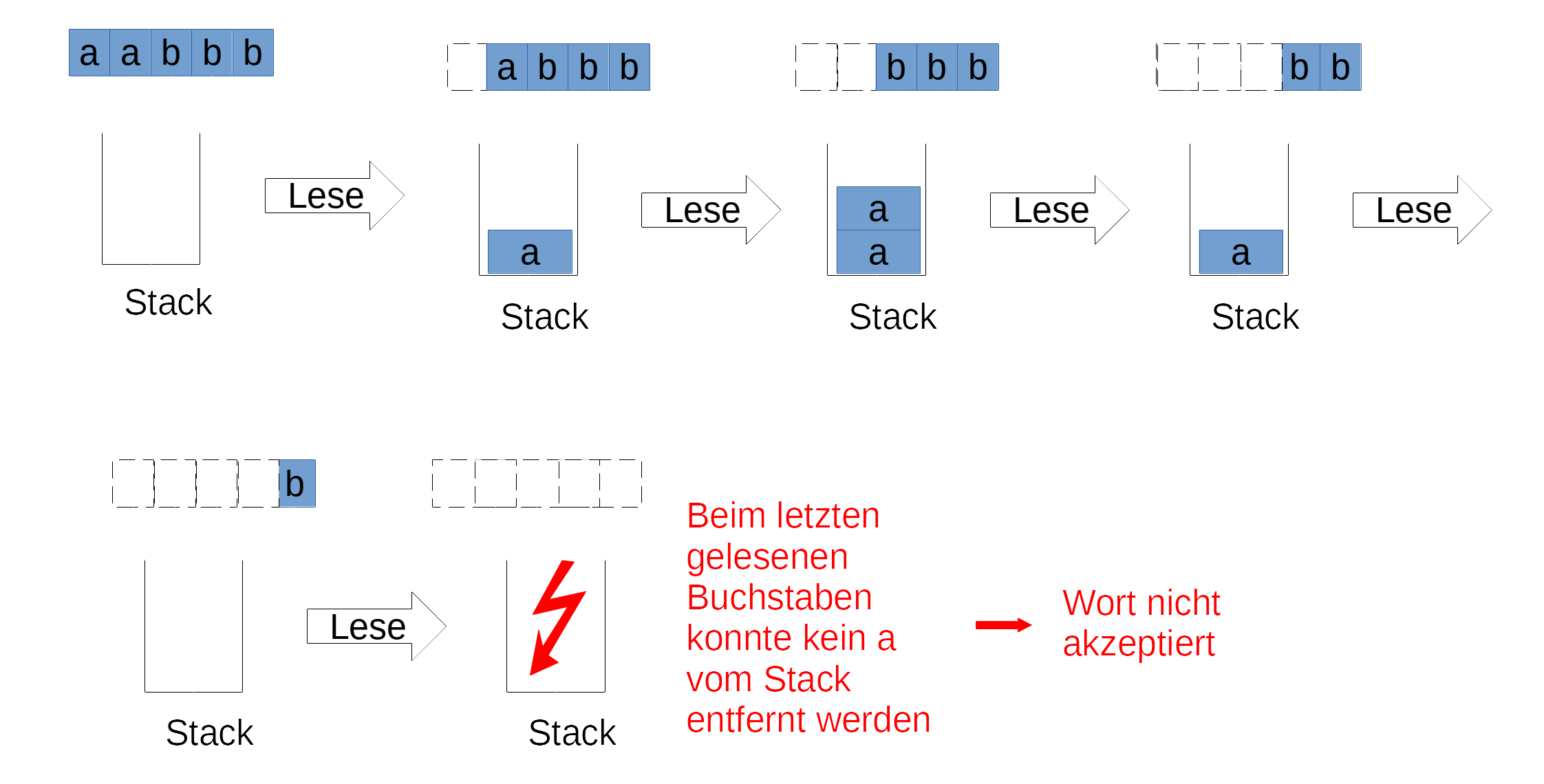
In folgendem Ablauf ist am Ende der Stack nicht leer, weil das Eingabewort zu wenig b's enthält.

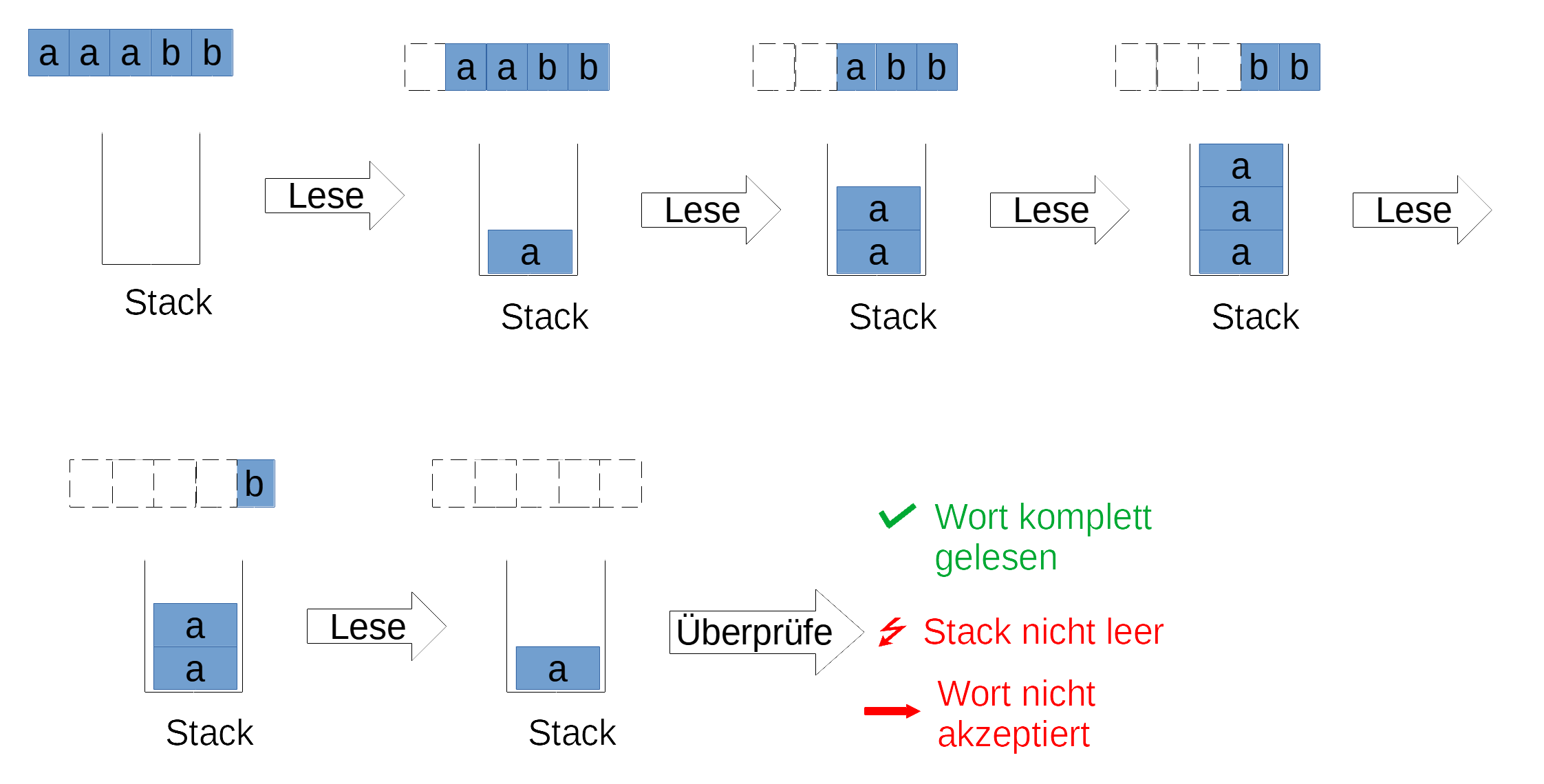
Der Stack ist unbegrenzt, du kannst also beliebig viele a's im Stack speichern.

Zustandsmenge, Übergangsrelation

Genau wie der endliche Automat hat auch der Stackautomat eine Zustandsmenge $Z$, und er hat einen Startzustand $q$; in den folgenden Beispielen ist dies immer der Zustand 0.

Die Übergangsrelation $d$ besteht beim endlichen Automaten aus Tripeln $(s, e, s')$, bestehend aus aktuellem Zustand $s$, gelesenem Eingabezeichen $e$ und Folgezustand $s'$. Beim Stackautomaten besteht die Übergangsrelation aus 5-Tupeln $(s, e, h, h', s')$ bestehend aus aktuellem Zustand $s,$ gelesenem Eingabezeichen $e$, vom Stack entferntem Zeichen $h$, neu auf dem Stack abgelegtem Zeichen $h'$ und Folgezustand $s'$.

Eine Besonderheit dabei: Sowohl $e$ als auch $h$ und $h'$ können gleich $\varepsilon$, also leer sein. Der Stackautomat kann also einen Zustandsübergang ausführen, ohne ein Zeichen $e$ einzulesen oder ohne ein Zeichen $h$ vom Stack zu entfernen oder ohne ein Zeichen $h'$ auf dem Stack abzulegen.

Beispielsweise ist $(1,\mathsf{a},\varepsilon,\mathsf{a},1)$ ein Tupel der Übergangsrelation des eben verwendeten Stackautomaten: Der Stackautomat befindet sich im Zustand 1, liest das Zeichen a, entfernt nichts vom Stack, legt das a auf dem Stack ab und bleibt im Zustand 1.

Außerdem ist $(1, \mathsf b, \mathsf a, \varepsilon, 2)$ ein Tupel der Übergangsrelation: Der Stackautomat befindet sich im Zustand 1, liest ein b, entfernt ein a vom Stack, legt nichts Neues auf dem Stack ab und geht in den Zustand 2 über.

Hier ist der wesentliche Teil der Übergangsrelation des Stackautomaten, der die Sprache $$ $L = \{\mathsf a^n\mathsf b^n ~|~ n \in\mathbb N \}$ erkennt, als Tabelle dargestellt:

$1 ~ \mathsf a ~ \varepsilon ~ \mathsf a ~ 1$

$1 ~ \mathsf b ~ \mathsf a ~ \varepsilon ~ 2$

$2 ~ \mathsf b ~ \mathsf a ~ \varepsilon ~ 2$

Der Stackautomat bleibt so lange im Zustand 1, wie er a's einliest und auf dem Stack ablegt. Sobald das erste b kommt, entfernt er ein a vom Stack und geht in den Zustand 2 über. Im Zustand 2 bleibt er so lange, wie er b's einliest und zugehörige a's vom Stack entfernt.

Der Stackautomat stoppt,

• wenn er das Eingabewort vollständig eingelesen hat, oder

• wenn er kein Tupel der Übergangsrelation anwenden kann.

Beispielsweise weiß der Stackautomat nicht weiter, wenn er im Zustand 2 ein a liest. Oder wenn er im Zustand 1 ein b liest, aber kein a auf dem Stack vorfindet. Dann stoppt er.

Genau wie der endliche Automat hat der Stackautomat eine Menge $F$ von Endzuständen. Wenn der Stackautomat das Eingabewort vollständig eingelesen hat und sich in einem Endzustand befindet, erkennt er das Eingabewort.

Damit der Stackautomat in einen Endzustand übergehen kann, wenn der Stack leer ist, muss er dies irgendwie erkennen. Der Trick ist, zu Beginn ein Stack-Ende-Zeichen $\$$ in den Stack zu schreiben. Wenn dann zum Schluss nur noch das Stack-Ende-Zeichen im Stack vorhanden ist, ist der Stack sozusagen leer, und der Stackautomat geht in einen Endzustand über.

Die so ergänzte, vollständige Übergangsrelation lautet somit

$0 ~ \varepsilon ~ \varepsilon ~ \$ ~ 1$

$1 ~ \mathsf a ~ \varepsilon ~ \mathsf a ~ 1$

$1 ~ \mathsf b ~ \mathsf a ~ \varepsilon ~ 2$

$2 ~ \mathsf b ~ \mathsf a ~ \varepsilon ~ 2$

$2 ~ \varepsilon ~ \$ ~ \varepsilon ~ 3^*$

Startzustand ist der Zustand 0. Mit dem ersten Tupel der Übergangsrelation schreibt der Stackautomat das Stack-Ende-Zeichen $\$$ in den Stack. Mit dem letzten Tupel erkennt der Stackautomat das Stack-Ende und geht in den Zustand 3 über. Der Zustand 3 ist ein Endzustand, hier mit einem * gekennzeichnet. Die Menge der Endzustände ist in diesem Fall also $F = \{3\}$.

Simuliere einmal diesen Stackautomaten mit unterschiedlichen Eingabewörtern auf der Seite https://hwlang.de/theor/stackautomat-anbn.htm.