Aufgaben zu vernetzten Strukturen
Mit diesen Übungsaufgaben lernst du das Arbeiten mit vernetzten Strukturen. Schaffst du sie alle?
- 1
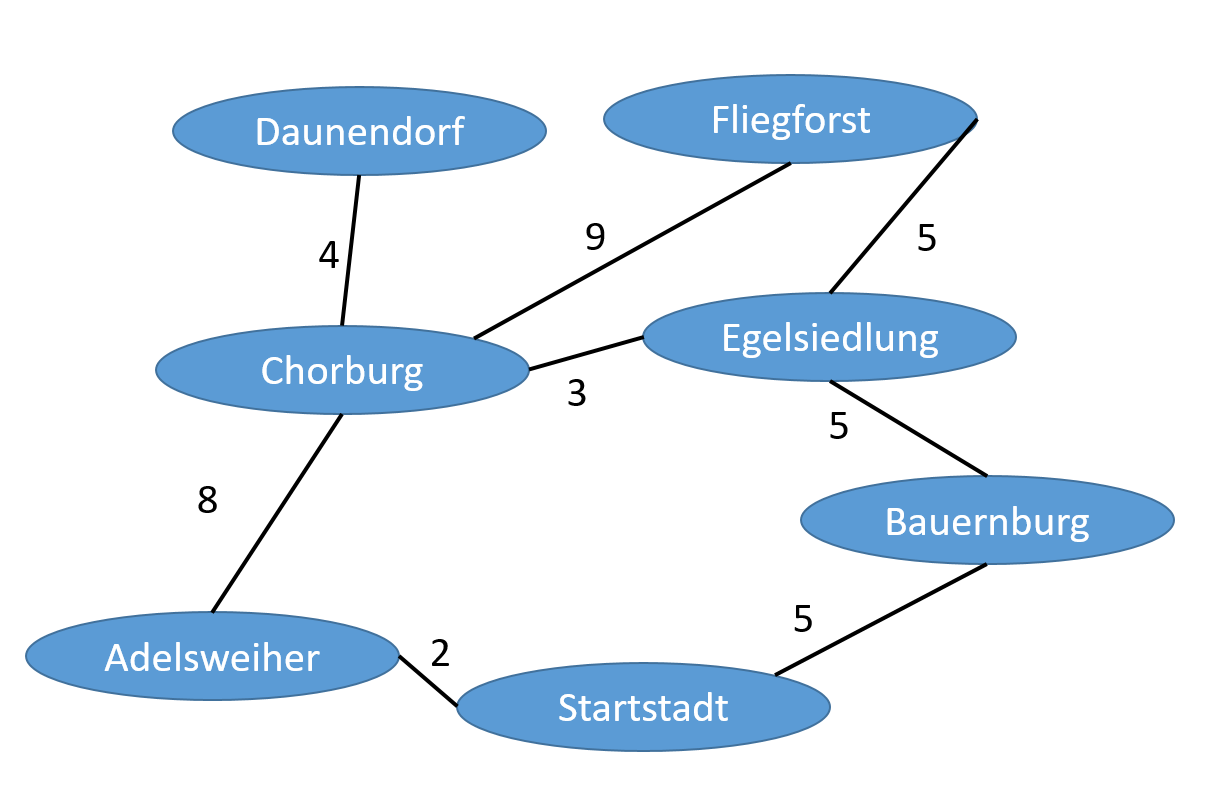
Bestimme die kürzesten Wege zu allen Orten ausgehend vom Startort "Startstadt"
Schnellkontrolle
Der letzte Ort, den man bei der kürzesten Strecke durchquert, bevor man Fliegforst erreicht, ist:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dijkstra Algorithmus (Kurs)
Vorbereitung: Tabelle mit allen Knoten
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
-
Bauernburg
-
Chorburg
-
Daunendorf
-
Egelsiedlung
-
Fliegforst
-
Startort als ersten akutellen Knoten festlegen und Nachbarn betrachten
Beginne bei Startstadt und betrachte alle Orte, die du von dort aus direkt erreichen kannst. Die neue Distanz zu diesen Knoten ist in jedem Fall kleiner als die bisherige und wird ersetzt:
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
2
Startstadt
Bauernburg
5
Startstadt
Chorburg
-
Daunendorf
-
Egelsiedlung
-
Fliegforst
-
Adelsweiher und seine Nachbarn betrachten
Sind alle Nachbarknoten von Startstadt in der Tabelle vermerkt, kannst du den nächsten aktiven Ort festlegen und dessen Nachbarn betrachten. Aus der Tabelle lernst du, dass Adelsweiher der Ort mit der kleinsten Distanz zum Startort ist, der noch nich besucht wurde. Chorburg erhält dadurch eine Distanz , da es von Adelsweiher aus erreicht werden kann:
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
2
Startstadt
Bauernburg
5
Startstadt
Chorburg
10
Adelsweiher
Daunendorf
-
Egelsiedlung
-
Fliegforst
-
Bauernburg und seine Nachbarn betrachten
Bauernburg ist der nächste unbesuchte Knoten, da er eine kleinere Distanz zum Startort hat als alle anderen bisher unbesuchten Knoten. Die Distanz zur Egelsiedlung verringert sich dadurch:
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
2
Startstadt
Bauernburg
5
Startstadt
Chorburg
10
Adelsweiher
Daunendorf
-
Egelsiedlung
10
Bauernburg
Fliegforst
-
Auswahl bei gleicher Distanz
Bei gleicher Distanz zweier unbesuchter Knoten zum Startort kann ein beliebiger der beiden ausgewählt werden. In dieser Lösung wird Chorburg ausgewählt.
Chorburg und seine Nachbarn betrachten
Betrachte alle vier Nachbarn von Chorburg und überprüfe für jeden, wie sich die Distanz verändert, wenn Chorburg der Vorgänger wäre. Adelsweiher ist selbst der Vorgänger, also kann sich die Distanz zu Adelsweiher über Chorburg nicht verkleinern. Zur Egelsiedlung ist die Distanz mit 11 größer als die bisherige (10) über Bauernburg, deshalb verändert sich hier nichts. Nach Daunendorf und Fliegfurst gibt es über Chorburg bessere Wege als die "bisher gefundenen":
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
2
Startstadt
Bauernburg
5
Startstadt
Chorburg
10
Adelsweiher
Daunendorf
14
Chorburg
Egelsiedlung
10
Bauernburg
Fliegforst
19
Chorburg
Egelsiedlung und seine Nachbarn betrachten
Die Distanz nach Chorburg über die Egelsiedlung ist mit 13 schlechter als die bisherige (10) und verändert sich nicht. Die Distanz nach Fliegforst über die Egelsiedlung verbessert sich allerdings auf 15 und wird in der Tabelle aktualisiert:
Knoten
Distanz
Vorgänger
Startstadt
0
-
Adelsweiher
2
Startstadt
Bauernburg
5
Startstadt
Chorburg
10
Adelsweiher
Daunendorf
14
Chorburg
Egelsiedlung
10
Bauernburg
Fliegforst
15
Egelsiedlung
Daunendorf und seine Nachbarn betrachten
Daunendorf hat keine Nachbarn außer dem Vorgänger Chorburg, deshalb verändert sich die Tabelle nicht.
Fliegforst und seine Nachbarn betrachten
Der Weg nach Chorburg über Fliegforst ist länger (Distanz: 24) als der bisherige über Adelsweiher (Distanz: 10) und wird deshalb nicht verändert.
Verwende den Dijkstra-Algorithmus, um alle kürzesten Wege systematisch zu ermitteln.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
