Textsuche: Knuth-Morris-Pratt-Algorithmus

Du suchst ein Muster $p$ der Länge $m$ in einem Text $t$ der Länge $n$ , wobei $m \ll n$ .

Mit dem naiven Algorithmus probierst du an jeder Stelle des Textes aus, ob das Muster dort übereinstimmt. Dies dauert im schlechtesten Fall $m \cdot n$ Schritte, etwa wenn das Muster aaaab und der Text aaaa…aaaaab lautet.

Der naive Algorithmus führt viele überflüssige Vergleiche durch. Der Knuth-Morris-Pratt-Algorithmus dagegen untersucht vorher in $m$ Schritten die Struktur des Musters, sodass er für die Suche anschließend nur noch $n$ Schritte benötigt.

Spielend einfach erklärt

Du verstehst den Knuth-Morris-Pratt-Algorithmus am besten, wenn du ihn als eine Art "Mensch-ärgere-dich-nicht-Spiel" betrachtest.

Aus beispielsweise dem Muster $p$ = ababaa leitest du direkt das folgende "Spielfeld" ab.

Spielregeln

Der erste Spielstein steht auf dem Startfeld 0. Nun wird reihum gewürfelt, mit einem Würfel, der mit Buchstaben beschriftet ist.

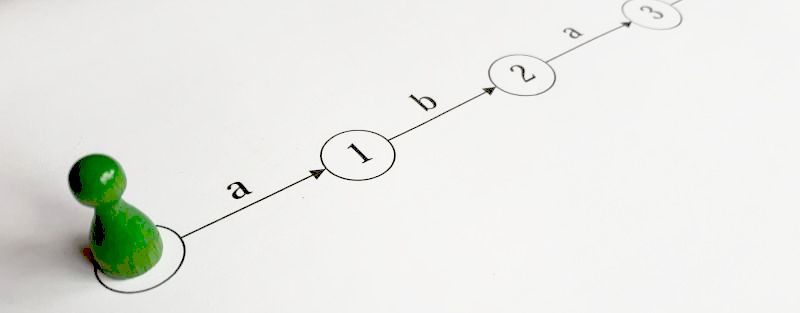
Ein Spieler, der ein a würfelt, darf den Spielstein auf Feld 1 "herausbringen". Gleichzeitig wird ein neuer Spielstein auf Feld 0 gestellt.

Der grüne Spielstein bleibt von nun an im Spiel, solange ein Buchstabe gewürfelt wird, mit dem er weiterrücken kann. Wenn also als nächstes ein b gewürfelt wird, darf er auf Feld 2 weiterrücken. Wenn danach ein a gewürfelt wird, darf er auf Feld 3 weiterrücken – und der Spieler, der das a gewürfelt hat, darf den gelben Spielstein auf Feld 1 herausbringen. Gleichzeitig wird ein neuer Spielstein auf Feld 0 gestellt.

Die folgende Abbildung zeigt die Spielsituation, nachdem die Buchstabenfolge aba gewürfelt worden ist.

Wenn danach erneut ein a gewürfelt wird, "fliegen" alle Spielsteine "raus", die mit dem a nicht weiterrücken können, also hier der gelbe und der grüne, sie werden vom Spielfeld entfernt. Jedoch darf der Spieler, der das a gewürfelt hat, den roten Spielstein auf Feld 1 herausbringen, und gleichzeitig wird ein neuer Spielstein auf Feld 0 gestellt.

So geht es die ganze Zeit weiter. Wird irgendwann im Verlauf des Spiels die Buchstabenfolge $p$ = ababaa gewürfelt, so erreicht ein Spieler mit seinem Spielstein das Zielfeld 6 und hat "gewonnen"! Das Spiel ist dann aber nicht vorbei, sondern es wird weiter gewürfelt, sodass andere Spieler auch noch "gewinnen" können.

Algorithmische Umsetzung

Tatsächlich werden die Buchstaben nicht gewürfelt, sondern die Buchstabenfolge ist der Text $t$ , in welchem die Vorkommen des Musters $p$ gesucht werden. Wenn ein Spieler "gewinnt", so ist ein Vorkommen des Musters im Text gefunden.

Wenn du den Knuth-Morris-Pratt-Algorithmus ausführst, simulierst du dieses Spiel. Der Clou dabei:

Du spielst nur mit dem am weitesten nach rechts fortgerückten Spielstein!

Du schaust jeweils, ob du diesen Spielstein mit dem nächsten Zeichen des Textes weiterziehen kannst.

Wenn ja, dann ziehst du ihn weiter.
Wenn nein, dann entfernst du ihn und spielst mit dem nächstfolgenden Spielstein weiter – wo dieser steht, schlägst du in einer sogenannten Fallback-Tabelle nach.

Es kann sein, dass du auch diesen nächstfolgenden Spielstein mit dem Zeichen des Textes nicht weiterziehen kannst. Dann entfernst du ihn und spielst mit dem als nächsten folgenden Spielstein weiter. Wo dieser steht, entnimmst du wieder der Fallback-Tabelle. Und so weiter.

Spätestens beim Feld 0 endet dieses Zurückfallen auf nächstfolgende Spielsteine. Auf Feld 0 steht immer ein Spielstein. Wenn du mit diesem nicht weiterziehen kannst, entfernst du ihn und stellst sofort wieder einen neuen Spielstein dorthin. Dann kommt das nächste Zeichen des Textes dran.

Zeitkomplexität

Du brauchst also nicht bei jedem Zeichen des Textes alle Spielsteine zu aktualisieren, sondern immer nur einen. Auf diese Weise benötigst du nur höchstens proportional zu $n$ viele Schritte, wobei $n$ die Länge des Textes $t$ ist.

Denn mit jedem der $n$ Zeichen des Textes rückst du einen Spielstein weiter, dies sind $n$ Schritte. Das gelegentliche Nachschlagen in der Fallback-Tabelle kostet zusammengenommen höchstens $n$ zusätzliche Schritte. Insgesamt sind dies also höchstens $2n$ Schritte.

Programm

Die folgende Funktion kmpSearch in der Programmiersprache Python implementiert das Verfahren. Die Indexposition $i$ zeigt auf das jeweilige Zeichen des Textes, $j$ zeigt auf das jeweilige Zeichen des Musters.

# Textsuche mit dem Knuth-Morris-Pratt-Algorithmus
def kmpSearch():
    # Muster p, Text t, Länge des Musters m, Länge des Textes n,
    # Fallback-Tabelle f
    global p, t, m, n, f
    i=0
    j=0
    while i<n:
        while j>=0 and p[j]!=t[i]:   # Mismatch, j kann nicht weiter
            j=f[j]   # Fallback
        i+=1
        j+=1
        if (j==m):   # Vorkommen gefunden
            report(i-j)
            j=f[j]    # j kann nicht weiter: Fallback

Verschiebung des Musters

Wenn der Index $j$ auf einen kleineren Wert $f[j]$ zurückfällt, entspricht dies einer Verschiebung des Musters nach rechts um $j-f[j]$ Positionen, zum Beispiel

a b a b a b a a b b a a …

a b a b a a

__ a b a b a a

________a b a b a a

Hier kommt es bei $i= 5$ und $j=5$ zu einem Mismatch. Daraufhin wird $j=f[5] = 3$ gesetzt. Das Muster wird um $5-3 = 2$ Positionen nach rechts geschoben, und es wird bei $i=6$ und $j=4$ weiterverglichen. Bei $i=8$ und $j=6$ wird ein Vorkommen des Musters gefunden und daraufhin $j = f[6]=1$ gesetzt. Das Muster wird daraufhin um $6-1 = 5$ Positionen nach rechts geschoben, usw.

Fallback-Tabelle berechnen

Jetzt brauchst du nur noch die Fallback-Tabelle zu berechnen.

Die Einträge der Fallback-Tabelle hängen nur vom Muster ab, nicht vom Text!

Wenn also zum Beispiel wie in der Abbildung der grüne Spielstein bis zum Feld 3 gekommen ist, dann steht zwangsläufig auf Feld 1 auch ein Spielstein. Das Fallback-Feld von Feld 3 ist somit das Feld 1. In der Fallback-Tabelle $f$ steht $f[3]=1$ .

Die Fallback-Tabelle berechnest du in einem Vorlauf aus dem Muster. Hierzu verwendest du wieder das Spielfeld wie eben. Das Eingabewort ist diesmal das Muster selber, also hier im Beispiel $p=$ ababaa.

Mit zwei Variablen $i$ und $j$ führst du dabei Buch über die Felder, auf denen der am weitesten und der am zweitweitesten fortgerückte Spielstein steht.

Das Feld $i$ ist jeweils das aktuelle Feld, das Feld $j$ ist das zugehörige Fallback-Feld. Zu jedem jeweils aktuellen Feld $i$ trägst du das zugehörige Fallback-Feld $j$ in die Fallback-Tabelle $f$ ein: $f[i]=j$ .

Da du das Muster selber als Eingabewort eingibst, kann der erste Spielstein bei jedem Zeichen weiterrücken; der zweite Spielstein fällt dagegen gelegentlich gemäß der schon berechneten Einträge der Fallback-Tabelle zurück.

Du beginnst mit dem Feld $i=0$ . Als Initialisierung trägst du $f[0]=-1$ in die Fallback-Tabelle ein.

Programm

Die folgende Funktion kmpPreprocess berechnet aus dem Muster die Fallback-Tabelle $f$ .

def kmpPreprocess():
    global p, t, m, n, f
    i=0
    j=-1
    f[i]=j
    while i<m:
        while j>=0 and p[j]!=p[i]:    # j kann nicht weiter
            j=f[j]   # fallback
        i+=1
        j+=1
        f[i]=j

Ganz entsprechend wie die Suchfunktion kmpSearch benötigt die Funktion kmpPreprocess höchstens $2m$ Schritte.

Die Funktion kmpPreprocess berechnet die Einträge der Fallback-Tabelle und greift dabei auf schon berechnete, gespeicherte Einträge zurück. Dieses Vorgehen ist ein schönes Beispiel für die algorithmische Technik der dynamischen Programmierung.

Hauptprogramm

Im Hauptprogramm legst du zunächst das Muster $p$ fest und rufst dann den Vorlauf kmpPreprocess auf, um die Fallback-Tabelle zu berechnen. Danach legst du den Text $t$ fest und rufst den Suchalgorithmus kmpSearch auf.

if __name__=="__main__":
    p="ababaa"
    m=len(p)
    f=(m+1)*[0]    # Fallback-Tabelle f mit Nullen vorbesetzen 
    kmpPreprocess()
    print(f)
    t="ababababaababaa"
    n=len(t)
    print(t)
    kmpSearch()

Die Funktion report implementierst du wie beim naiven Algorithmus.

def report(i):
    print(i*" " + p)

Die entsprechende Ausgabe zeigt dir dann die Positionen, an denen das Muster im Text vorkommt.

a b a b a b a b a a b a b a a

____ a b a b a a

__________a b a b a a

Probiere das Programm einmal mit unterschiedlichen Texten und Mustern aus!

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?