Wenn du zwei -Bit-Zahlen nach der Schulmethode miteinander multiplizierst, dann benötigst du hierfür Schritte. Aber es geht schneller: in nur Schritten, mit dem Karatsuba-Algorithmus. Die Idee ist bestechend einfach, die rekursive Implementierung ist unkompliziert.
Der Computer ist schnell – eine Multiplikation von zwei ganzen Zahlen schafft er in Nullkommanix.
Dies gilt für die Zahlen, mit denen der Computer normalerweise rechnet, nämlich für relativ "kleine" Zahlen, die nicht größer als ca. 2 Milliarden sind. Dies sind Zahlen, die im Binärformat mit 32 Bit dargestellt werden. Das Rechenwerk des Computers kann 32-Bit-Zahlen in einem Schritt miteinander multiplizieren.
Was ist aber, wenn die Zahlen nicht 32 Bit lang sind, sondern zum Beispiel 1024 Bit oder gar 2048 Bit? Und wenn nicht nur eine Multiplikation ausgeführt wird, sondern tausende?
Multiplikation mit der Schulmethode
Wenn du zwei -Bit-Zahlen nach der Schulmethode multiplizierst, dann füllst ein parallelogrammförmiges Schema mit Einträgen aus, dafür benötigst du mindestens Schritte. In der Abbildung ist dieses Schema für zwei 4-Bit-Zahlen dargestellt.
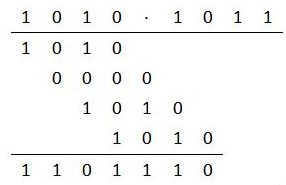
Multiplikation mit der Schulmethode
Karatsuba-Algorithmus
Tatsächlich geht es schneller: Mit dem Karatsuba-Algorithmus benötigst du statt Schritten nur Schritte.
Vielleicht ist dein erster Gedanke, dass 1,585 nicht so furchtbar viel weniger als 2 ist – das stimmt, aber im Exponenten wirkt sich der geringe Unterschied gehörig aus. Anhand folgender Tabelle bekommst du einen Eindruck davon:
1024 | < 60.000 | > 1.000.000 |
Für die Multiplikation von zwei 1024 Bit langen Zahlen benötigst du mit dem Karatsuba-Algorithmus weniger als 60.000 Schritte, mit der Schulmethode dagegen mehr als eine Million Schritte.
Kommen denn so lange Zahlen in der Praxis überhaupt vor? Ja, in der Kryptografie sind zum Beispiel bei der RSA-Verschlüsselung die verwendeten Zahlen mindestens 1024 Bit lang, meist sogar 2048 Bit lang. Und du benötigst dabei eine Vielzahl von Multiplikationen dieser Zahlen, um einen Text zu verschlüsseln.
Divide-and-Conquer-Strategie
Dein Ziel ist es, zwei -Bit-Zahlen in weniger als Schritten zu multiplizieren. Du gehst nach der Divide-and-Conquer-Strategie vor.
Divide
Du unterteilst die beiden -Bit-Zahlen und jeweils in zwei Hälften , sowie , . Diese Teilstücke sind jetzt nur noch Bit lang - wenn du zwei dieser Teilstücke miteinander multiplizierst, benötigst du nur Schritte.

Conquer
Es gilt sowie , hierbei ist . Durch Ausmultiplizieren erhältst du
Leider ist es so, dass die 4 Multiplikationen zu je Schritten zusammen auch wieder Schritte ergeben – also ist nichts gewonnen…
Die Idee von Karatsuba
Tatsächlich schaffst du es auch mit 3 Multiplikationen. Du brauchst ein paar Additionen und Subtraktionen zusätzlich, diese verursachen aber höchstens linearen Aufwand und fallen damit nicht ins Gewicht. Wenn du lange genug herumprobierst, kommst du auf folgende Lösung:
Du berechnest die 3 Produkte
und setzt daraus folgendermaßen zusammen
Die Produkte und berechnest du dabei nur einmal und verwendest sie mehrfach.
Eigentlich nicht schwer, oder? Bereits im Jahre 1960 fand der damals 23-jährige russische Mathematiker A. Karatsuba diese Lösung.
Rekursive Implementierung
Die 3 Produkte , und berechnest du wieder nach derselben Methode: Du unterteilst die Operanden jeweils in zwei Hälften, usw.
Irgendwann kannst du die Operanden nicht mehr unterteilen, nämlich wenn sie nur noch 1 Bit lang sind. Dann multiplizierst du die Bits direkt.
In der Praxis brichst du bei der Langzahlen-Multiplikation die Rekursion ab, wenn du die Operanden mit dem Standard-Multiplikationsbefehl des Computers multiplizieren kannst, also bei einer Länge von 32 oder 64 Bit.
Zeitkomplexität
Für die Zeitkomplexität ausschlaggebend sind die Multiplikationen. Du zählst somit die Schritte, die du für die Multiplikationen benötigst.
Für die Multiplikation von 1-Bit-Zahlen benötigst du 1 Schritt.
Für die Multiplikation von 2-Bit-Zahlen benötigst du 3 Multiplikationen von 1-Bit-Zahlen, also 3 Schritte.
Für die Multiplikation von 4-Bit-Zahlen benötigst du 3 Multiplikationen von 2-Bit-Zahlen, also Schritte.
Für die Multiplikation von 8-Bit-Zahlen benötigst du 3 Multiplikationen von 4-Bit-Zahlen, also Schritte.
Jetzt erkennst du das System:
Für die Multiplikation von -Bit-Zahlen benötigst du Schritte.
Verrückterweise gilt
Somit erhältst du
Fazit
Der Karatsuba-Algorithmus ist ein besonders schönes Beispiel für die Anwendung der Divide-and-Conquer-Strategie.
Du erinnerst dich: Die Divide-and-Conquer-Strategie besteht aus den drei Phasen
Divide - zerteile das Problem in kleinere Teilprobleme
Conquer - löse die Teilprobleme
Combine - füge die Lösungen der Teilprobleme zur Lösung des ursprünglichen Problems zusammen
Beim Karatsuba-Algorithmus ist es entscheidend, dass die vier Teilprobleme in der Conquer-Phase mit nur drei Multiplikationen gelöst werden.
