1 Übersicht
Hier lernst du
wie man Schnittpunkte der Graphen von gebrochen rationalen Funktionen mit der - und der -Achse bestimmt
wie man Schnittpunkte von zwei Graphen bestimmen kann
wie man dies auf Sachaufgaben anwenden kann
Du solltest schon wissen:
was eine gebrochen rationale Funktion ist
was eine lineare Funktion ist
wie man Bruchterme vereinfacht
wie man Bruchgleichungen löst
2 Computerherstellung
Ein kleines Unternehmen stellt Computer her. Die Abteilung für die Produktion stellt fest, dass die Herstellungskosten von einem Computer stark von der Stückzahl, die insgesamt produziert werden abhängt.
Wenn also mehr Computer hergestellt werden, wird der Herstellungspreis pro Stück niedriger.
Sie bestimmen die folgende Formel, um die Kosten pro Computer () in Abhängigkeit der Stückzahl () zu bestimmen.

Die Marktforschungsabteilung hat herausgefunden, dass man diese Art von Computer zu einem Preis von verkaufen sollte, da sie sonst vom Kunden als zu teuer angesehen werden.
Die Geschäftsleitung fragt sich nun: Wie viele Computer müssen wir mindestens produzieren und verkaufen, dass sich das für uns lohnt?
3 Schnittpunkte graphisch bestimmen
Was Schnittpunkte von Graphen von gebrochen rationalen Funktionen eigentlich sind und wie man sie graphisch bestimmt, siehst du im Video.
Schnittpunkte graphisch bestimmen:
Zeichnen beider Graphen, je genauer, desto besser das Ergebnis
Schnittpunkt(e) auslesen: - und - Koordinate bestimmen!
4 Übungsaufgaben: graphische Bestimmung
Laden
5 Schnittpunkte rechnerisch bestimmen
Um ein genaueres Ergebnis zu erhalten, kann man den Schnittpunkt auch ausrechnen.
Am Schnittpunkt sind und -Wert beider Funktionen gleich.
Um den Schnittpunkt zu erhalten, setzt man die Funktionsterme gleich.
Zur Wiederholung:
bei ist der y-Wert:
Bei unserem Beispiel sieht das also so aus:
Der y-Wert von muss gleich der Geraden sein.
Lässt man das weg, so erhält man eine Bruchgleichung. Löse diese!
Der Schnittpunkt befindet sich also bei dem -Wert .
Wenn die Firma mehr als Rechner herstellt (also mehr als ), so macht sie Gewinn.
Der Schnittpunkt hat auch noch eine -Koordinate. Dazu setzt man den -Wert wieder in eine der Funktionen ein. Hier ist das einfach, da die eine Funktion ist!
Der Schnittpunkt ist also
Ab einer verkauften Stückzahl von Computern macht die Firma also Gewinn.
Schnittpunkte rechnerisch bestimmen:
Setze die beiden Funktionen, deren Schnittpunkt du finden möchtest, gleich.
Löse anschließend nach dem -Wert auf.
Setze den -Wert in eine der beiden Funktionen ein, um den -Wert des Schnittpunkts zu erhalten.
Schreibe einen Antwortsatz oder halte den Schnittpunkt in der Form fest.
6 Schnittpunkte mit den Koordinatenachsen
In vielen Aufgaben wird nach den Schnittpunkten mit den Koordinatenachsen gefragt.
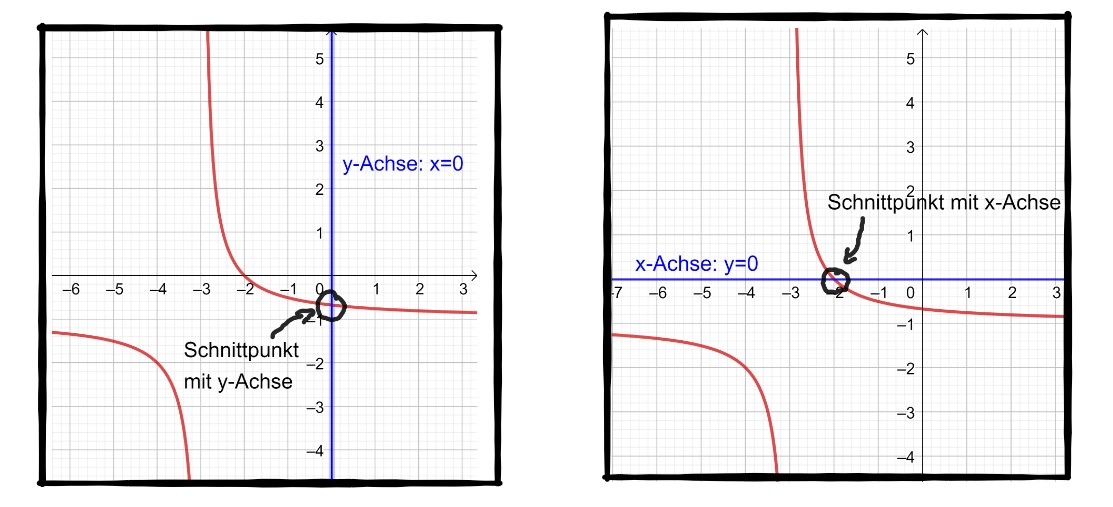
Die -Achse kann man auch als Funktion ausdrücken. Die -Achse wird durch beschrieben.
Die Schnittpunkte mit der -Achse kann man also so ausrechnen, wie du es in den letzten Aufgaben schon gemacht hast.
Die Schnittpunkte mit der -Achse () bestimmst du, indem du in die Funktion (z.B. ) für die null einsetzt () und den Funktionswert berechnest.
Beispiel:
Bestimmen wir zunächst den Schnittpunkt mit der -Achse (die Nullstelle der Funktion):
Dies ist der Schnittpunkt von und :
Man kann also folgende Bruchgleichung aufstellen:
Diese wird nun nach aufgelöst:
Der Schnittpunkt mit der -Achse liegt also bei und .
Der Schnittpunkt mit der -Achse wird bestimmt, indem man in die Funktion einsetzt:
Der Schnittpunkt mit der -Achse:
7 Übungsaufgaben rechnerische Bestimmung
Laden
Laden
Laden
8 Zusammenfassung
Schnittpunkte von gebrochen rationalen Funktionen mit anderen Funktionen können graphisch oder rechnerisch gelöst werden.
Graphische Lösung: (ungenauer als die rechnerische Lösung)
Zeichne beide Graphen in ein Koordinatensystem
Lies alle Schnittpunkte der Graphen ab
Rechnerische Lösung:
Am Schnittpunkt sind - und -Wert gleich.
Setze die Funktionsterme gleich und löse nach auf.
Setze den -Wert in eine der Funktionen ein, um auf den -Wert zu kommen.
Schnittpunkte mit den Koordinatenachsen:
Mit der -Achse: Berechne den Schnittpunkt des Graphen mit
Mit der -Achse: Setze in den Funktionsterm ein, um auf den -Wert zu kommen.
