Wir haben die Struktur der Vektorräume kennengelernt und verschiedene Eigenschaften von ihnen untersucht. Nun wollen wir Vektorräume nicht nur isoliert voneinander betrachten, sondern auch Abbildungen zwischen ihnen. Manche dieser Abbildungen vetragen sich gut mit der zugrundeliegenden Vektorraumstruktur und werden deswegen lineare Abbildungen oder Vektorraumhomomorphismen genannt.

Dass wir solche strukturerhaltenden Abbildungen untersuchen, ist eine typische Vorgehensweise der Algebra. Für viele algebraische Strukturen wie Gruppen, Ringe oder Körper untersucht die Algebra die dazugehörigen strukturerhaltenden Abbildungen zwischen den jeweiligen algebraischen Strukturen – Gruppenhomomorphismen, Ringhomomorphismen und Körperhomomorphismus. Bei Vektorräumen sind die strukturerhaltenden Abbildungen die linearen Abbildungen bzw. die Vektorraumhomomorphismen.

Seien also $V$ und $W$zwei Vektorräume. Wann ist eine Abbildung $f:V\to W$ strukturerhaltend bzw. verträgt sich gut mit den zugrundeliegenden Vektorraumstrukturen in $V$ und $W$? Wiederholen wir hierzu, was die Vektorraumstruktur ausmacht: Vektorräume sind Strukturen, in denen zwei Operationen möglich sind:



• Addition von Vektoren: Zwei Vektoren können miteinander addiert werden, wobei die Addition der Addition von Zahlen in ihren Eigenschaften ähnelt.

• Skalare Multiplikation: Vektoren können mit einem Skalierungsfaktor aus einem Körper skaliert (gestaucht, gestreckt oder gespiegelt) werden.

Beginnen wir mit der Addition von Vektoren: Wann verträgt sich eine Funktion $f:V\to W$ mit den Additionen ${+}_{{}_V}$ und ${+}_{{}_W}$ auf den jeweiligen Vektorräumen $V$ und $W$? Hier kann man folgende Hypothese aufstellen:

Eine Abbildung ist verträglich mit der Addition, wenn eine Summe durch die Abbildung erhalten bleibt. Wenn also $v_3=v_1{+}_{{}_V}{v}_2$ im Vektorraum $V$ eine Summe ist, so bilden auch die Bilder von $v_1$ , $v_2$ und $v_3$ im Vektorraum $W$ eine entsprechende Summe: $f(v_3)=f(v_1){+}_{{}_W}f(v_2)$

Eine mit der Addition verträgliche Abbildung erfüllt somit für alle $v_1,v_2,v_3\in V$die Implikation:

$v_3=v_1{+}_{{}_V}{v}_2⟹f(v_3)=f(v_1){+}_{{}_W}f(v_2)$

Diese Implikation kann in einer Gleichung zusammengefasst werden, indem die Prämisse $v_3=v_1{+}_{{}_V}{v}_2$ in die zweite Gleichung eingsetzt wird. Es soll also für alle $v_1,v_2\in V$ gelten:

$f(v_1{+}_{{}_V}{v}_2)=f(v_1){+}_{{}_W}f(v_2)$

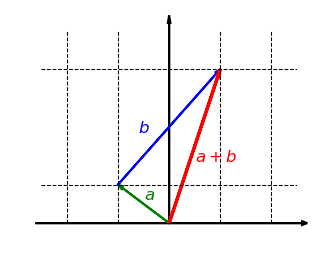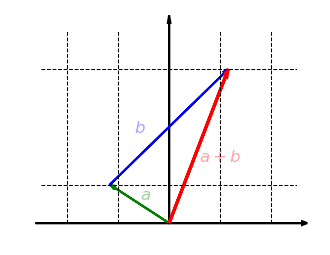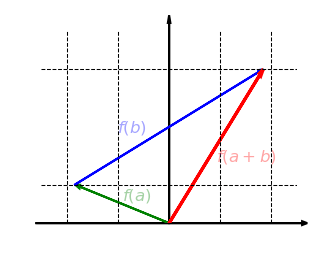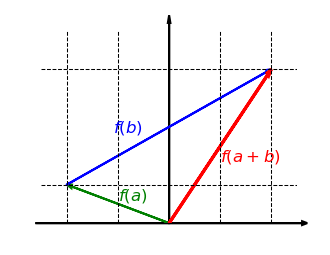
Diese Gleichung beschreibt die charakteristische Eigenschaft der linearen Abbildung, verträglich zur Vektoraddition zu sein. Wir können sie auch gut für Abbildungen ${ℝ}^2\to {ℝ}^2$ visualisieren. Eine Abbildung verträgt sich genau dann mit der Addition, wenn das durch die Vektoren $v_1$, $v_2$ und $v_3=v_1{+}_{{}_V}{v}_2$ gegebene Dreieck im Definitionsbereich durch die Abbildung erhalten bleibt. Sprich: Auch die drei Vektoren $f(v_1)$, $f(v_2)$ und $f(v_3)=f(v_1{+}_{{}_V}{v}_2)$ bilden ein (Additions-)Dreieck:

Wenn $f$ sich nicht mit der Addition verträgt, gibt es Vektoren $v_1$ und $v_2$ mit $f(v_1{+}_{{}_V}{v}_2)\ne f(v_1){+}_{{}_W}f(v_2)$. Das durch $v_1$, $v_2$ und $v_3=v_1{+}_{{}_V}{v}_2$ erzeugte Dreieck bleibt dann nicht erhalten, weil die Dreiecksseite $v_1{+}_{{}_V}{v}_2$ des Ausgangsdreiecks nicht auf die Dreiecksseite $f(v_1){+}_{{}_W}f(v_2)$ des Zieldreiecks abgebildet wird:

Analog können wir uns überlegen, dass eine Abbildung $f:V\to W$ genau dann verträglich mit der skalaren Multiplikation, wenn diese durch die Abbildung erhalten bleibt. Es sollte also für alle $w,v\in V$ und für alle Skalare $\lambda \in K$ gelten:

$w=\lambda {\cdot }_{{}_V}v⟹f(w)=\lambda {\cdot }_{{}_W}f(v)$

Beachte, dass $\lambda$ ein Skalar und kein Vektor ist und damit nicht durch die betrachtete Funktion veändert wird. Damit wir in der obigen Implikation denselben Skalar verwenden können, müssen beide Vektorräume denselben zugrundeliegenden Körper haben. Sowohl der Definitionsbereich $V$ als auch der Wertebereich $W$ muss ein $K$-Vektorraum sein.

Lineare Abbildungen erhalten also Skalierungen. Aus $w=\lambda v$ folgt $f(w)=\lambda f(v)$. Für den Fall, dass $f(v)\ne 0$ ist, werden Geraden der Form $\{\lambda v:\lambda \in ℝ\}$ auf die Gerade $${\displaystyle \{\lambda f(v):\lambda \in ℝ\}}$$ abgebildet. Obige Implikation kann in eine Gleichung zusammengefasst werden. Es soll also für alle $v\in V$ und $\lambda \in K$ gelten:

$f(\lambda {\cdot }_{{}_V}v)=\lambda {\cdot }_{{}_W}f(v)$

Für Abbildungen ${ℝ}^2\to {ℝ}^2$ bedeutet dies, dass ein skalierter Vektoren $\lambda {\cdot }_{{}_V}v$ auf die entsprechende Skalierung $\lambda {\cdot }_{{}_W}f(w)$ des Bildvektors abgebildet wird:

Wenn eine Abbildung nicht verträglich zur skalaren Multiplikation ist, so gibt es einen Vektor $v$ und einen Skalierungsfaktor $\lambda$ , so dass $f(\lambda {\cdot }_{{}_V}v)\ne \lambda {\cdot }_{{}_W}f(w)$ ist:

Eine lineare Abbildung ist eine spezielle Abbildung zwischen Vektorräumen, die sich mit der Struktur der zugrundeliegenden Vektorräumen verträgt. Dies bedeutet insbesondere, dass eine lineare Abbildung $f:V\to W$ die beiden folgenden charakteristischen Eigenschaften besitzt:

• Verträglichkeit mit der Addition: $\forall v_1,v_2\in V:f(v_1{+}_{{}_V}{v}_2)=f(v_1){+}_{{}_W}f(v_2)$

• Verträglichkeit mit der skalaren Multiplikation: $\forall v\in V,\lambda \in K:f(\lambda {\cdot }_{{}_V}v)=\lambda {\cdot }_{{}_W}f(v)$

Die Verträglichkeit mit der Addition nennt man Additivität und die Verträglichkeit mit der skalaren Multiplikation wird Homogenität genannt

Hinweis

In der Literatur wird für den Begriff lineare Abbildung auch der Begriff Vektorraumhomomorphismus oder kurz Homomorphismus genutzt. Das altgriechische Wort homós steht für „gleich“, morphé steht für „Form“. Wörtlich übersetzt ist ein Vektorraumhomomorphismus also eine Abbildung zwischen Vektorräumen, welche die „Form“ der Vektorräume gleich lässt.

Die charakteristischen Gleichungen der linearen Abbildung sind $f(v_1+v_2)=f(v_1)+f(v_2)$ und $f(\lambda \cdot v)=\lambda \cdot f(v)$. Was bedeuten diese beiden Eigenschaften intuitiv? Nach der Additivitätseigenschaft ist es egal, ob man $v_1$ und $v_2$ zuerst addiert und dann abbildet oder ob man beide Vektoren erst abbildet und dann addiert. Beide Wege führen zum selben Ergebnis:

Was besagt die Homogenitätseigenschaft? Unabhängig davon ob man zuerst $v$ mit $\lambda$ multipliziert und dann abbildet oder den Vektor erst abbildet und dann mit $\lambda$ multipliziert, ist das Ergebnis das Gleiche:

Die charakteristischen Eigenschaften der linearen Abbildungen verdeutlichen also, dass die Reihenfolge der Funktionsabbildung und der Vektorraumoperationen egal ist.

Unser erstes Beispiel ist die Streckung um den Faktor $\beta$ in $x$-Richtung in der Ebene ${ℝ}^2$. Dabei wird jeder Vektor $a=(a_x,a_y{)}^T\in {ℝ}^2$ abgebildet auf $f(a)=(\beta a_x,a_y{)}^T$. Die folgende Grafik zeigt diese Abbildung für $\beta =2$. Die $y$-Koordinate bleibt dabei gleich und die $x$-Koordinate wird verdoppelt:

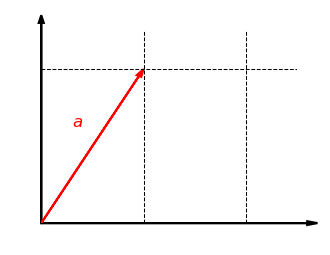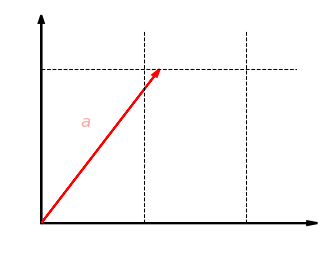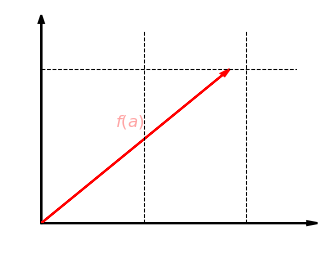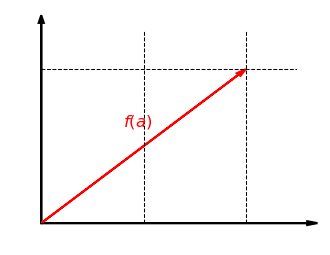
Schauen wir uns nun an, ob diese Abbildung verträglich mit der Addition ist. Nehmen wir also zwei Vektoren $a$ und $b$, bilden die Summe $a+b$ und strecken diese dann in $x$-Richtung. Das Ergebnis ist dasselbe, als wenn wir beide Vektoren zuerst in $x$-Richtung strecken und dann addieren:

Das lässt sich auch mathematisch zeigen. Unsere Abbildung ist die Funktion $f:{ℝ}^2\to {ℝ}^2,f((x,y{)}^T)=(\beta x,y{)}^T$. Wir können nun die Eigenschaft $f(a+b)=f(a)+f(b)$ nachprüfen:

$\begin{array}{cl}f(a+b)& =f(\left(\begin{array}{c}{a}_x\\ a_y\end{array}\right)+\left(\begin{array}{c}{b}_x\\ b_y\end{array}\right))\\ & =f\left(\left(\begin{array}{c}{a}_x+b_x\\ a_y+b_y\end{array}\right)\right)\\ & =\left(\begin{array}{c}\beta (a_x+b_x)\\ a_y+b_y\end{array}\right)\\ & =\left(\begin{array}{c}\beta a_x+\beta b_x\\ a_y+b_y\end{array}\right)\\ & =\left(\begin{array}{c}\beta a_x\\ a_y\end{array}\right)+\left(\begin{array}{c}\beta b_x\\ b_y\end{array}\right)\\ & =f\left(\left(\begin{array}{c}{a}_x\\ a_y\end{array}\right)\right)+f\left(\left(\begin{array}{c}{b}_x\\ b_y\end{array}\right)\right)\\ & =f(a)+f(b)\end{array}$

Schauen wir uns nun die Verträglichkeit mit der skalaren Multiplikation an. Die folgende Grafik zeigt, dass es egal ist, ob der Vektor $a$ zuerst mit einem Faktor $\lambda$ skaliert und dann in $x$-Richtung gestreckt wird oder zuerst in $x$-Richtung gestreckt und dann mit $\lambda$ skaliert wird:

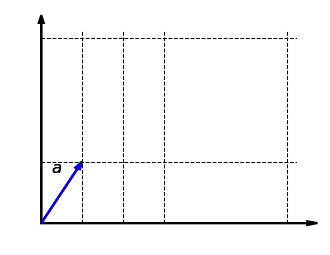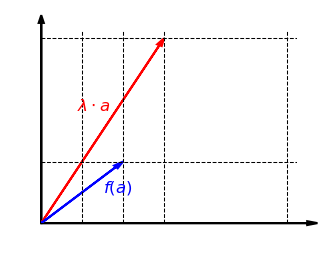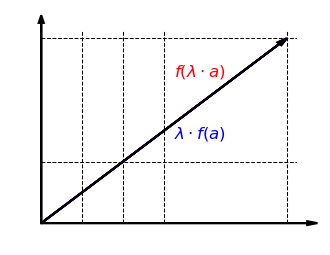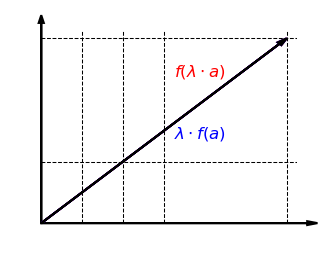
Auch das lässt sich formal zeigen: Für $a\in {ℝ}^2$ und \lambda $\in ℝ$ gilt

$\begin{array}{cl}f(\lambda a)& =f\left(\lambda \left(\begin{array}{c}{a}_x\\ a_y\end{array}\right)\right)=f\left(\left(\begin{array}{c}\lambda a_x\\ \lambda a_y\end{array}\right)\right)\\ & =\left(\begin{array}{c}\beta (\lambda a_x)\\ \lambda a_y\end{array}\right)=\left(\begin{array}{c}\lambda \beta a_x\\ \lambda a_y\end{array}\right)\\ & =\lambda \left(\begin{array}{c}\beta a_x\\ a_y\end{array}\right)=\lambda f\left(\left(\begin{array}{c}{a}_x\\ a_y\end{array}\right)\right)\\ & =\lambda f(a).\end{array}$

Damit ist unser f eine lineare Abbildung.

Im Folgenden betrachten wir eine Drehung $D_{\alpha }$ der Ebene um den Winkel $\alpha$ (gegen den Uhrzeigersinn gemessen) mit dem Ursprung als Drehzentrum. Es handelt sich dabei also um eine Abbildung $D_{\alpha }:{ℝ}^2\to {ℝ}^2$, die jedem Vektor $v\in {ℝ}^2$ den um den Winkel $\alpha$ gedrehten Vektor $D_{\alpha }(v)\in {ℝ}^2$ zuordnet:

Wir wollen uns jetzt davon überzeugen, dass $D_{\alpha }$ eine lineare Abbildun ist. Dazu müssen wir zeigen:

1. $D_{\alpha }$ ist additiv: Für alle $v,w\in {ℝ}^2$ ist $D_{\alpha }(v+w)=D_{\alpha }(v)+D_{\alpha }(w)$.

2. $D_{\alpha }$ ist homogen: Für alle $v\in {ℝ}^2$ und $\lambda \in ℝ$ ist $D_{\alpha }(\lambda \cdot v)=\lambda \cdot D_{\alpha }(v)$.

Überprüfen wir zunächst die Additivität, also die Gleichung $D_{\alpha }(v+w)=D_{\alpha }(v)+D_{\alpha }(w)$. Addieren wir zwei Vektoren $v,w\in {ℝ}^2$ zuerst und drehen ihre Summe v+w anschließend um den Winkel $\alpha$, so soll derselbe Vektor herauskommen, wie wenn wir erst die Vektoren um den Winkel $\alpha$ drehen und im Anschluss die gedrehten Vektoren $D_{\alpha }(v)$ und $D_{\alpha }(w)$ addieren. Dies machen wir uns an folgenden beiden Videos klar:

Kommen wir nun zur Homogenität: $D_{\alpha }(\lambda \cdot v)=\lambda \cdot D_{\alpha }(v)$. Strecken wir zunächst einen Vektor $v\in {ℝ}^2$ um einen Faktor $\lambda \in ℝ$ und drehen das Resultat $\lambda \cdot v$ danach um den Winkel $\alpha$, so soll derselbe Vektor herauskommen, wie wenn wir als Erstes die Drehung um den Winkel $\alpha$ durchführen und daraufhin das Ergebnis $D_{\alpha }(v)$ um den Faktor $\lambda$ skalieren. Auch dies wird durch zwei Videos ersichtlich:

Somit handelt es sich bei Drehungen im ${ℝ}^2$ um lineare Abbildungen.

Lineare Funktionen wurden in der Schule als Funktionen der Form $f(x)=mx+t$ mit $m,t\in ℝ$ eingeführt. Es handelt sich dabei nicht um lineare Abbildungen. Sie sind es nur für $t=0$. So ist zum Beispiel für $m=1$ und $t=2$:

$f(x+y)=x+y+2\ne x+y+2+2=f(x)+f(y)$

Dass die in der Schule geläufigen linearen Funktionen dennoch etwas mit den linearen Abbildungen zu tun haben, wird einem klar, wenn man die linearen Abbildungen von $f:ℝ\to ℝ$ betrachtet. Diese sind Abbildungen der Form $f(x)=mx$ mit $m\in ℝ$. Die Funktionen der Form $f(x)=mx+t$ aus der Schule sind sogenannte affin-lineare Abbildungen: Sie sind die Summe einer linearen Abbildung und eines konstanten Terms $t$

Affine Abbildung bilden Geraden auf Geraden ab und erhalten dabei Parallelität und Teilverhältnisse von Strecken.

Wir können jede affine Abbildunge $x\mapsto A(x)$ immer in eine lineare Abbildung $x\mapsto L(x)$ und eine Translation $x\mapsto x+t$ zerlegen. Es gilt also $A(x)=L(x)+t$. Weil die Translationen $x\mapsto x+t$ einfach zu beschreiben sind, ist der lineare Teil meistens interessanter. In der Theorie schauen wir uns deswegen nur den linearen Teil an, um nicht das $x+t$ mitzuschleppen.

Lineare Funktionen wurden in der Schule als Funktionen der Form $f(x)=mx+t$ mit $m,t\in ℝ$. Es handelt sich dabei nicht um lineare Abbildungen. Sie sind es nur für $t=0$. So ist zum Beispiel für $m=1$ und $t=2$:

Dass die in der Schule geläufigen linearen Funktionen dennoch etwas mit den linearen Abbildungen zu tun haben, wird einem klar, wenn man die linearen Abbildungen von $f:ℝ\to ℝ$ betrachtet. Diese sind Abbildungen der Form $f(x)=mx$ mit $m\in ℝ$. Die Funktionen der Form $f(x)=mx+t$ aus der Schule sind sogenannte affin-lineare Abbildungen: Sie sind die Summe einer linearen Abbildung und eines konstanten Terms $t.$

Affine Abbildung bilden Geraden auf Geraden ab und erhalten dabei Parallelität und Teilverhältnisse von Strecken.

Wir können jede affine Abbildunge $x\mapsto A(x)$ immer in eine lineare Abbildung $x\mapsto L(x)$ und eine Translation $x\mapsto x+t$ zerlegen. Es gilt also $A(x)=L(x)+t$. Weil die Translationen $x\mapsto x+t$ einfach zu beschreiben sind, ist der lineare Teil meistens interessanter. In der Theorie schauen wir uns deswegen nur den linearen Teil an, um nicht das $x+t$ mitzuschleppen.

Als nächstes untersuchen wir, ob es auch nicht lineare Abbildungen gibt. Hierzu betrachten wir die Normabbildung auf der Ebene, die jedem Vektor seine Länge zuordnet:

Diese Abbildung ist keine lineare Abbildung, denn sie erhält weder die Vektoraddition noch die Skalarmultiplikation.

Dies zeigen wir mit Hilfe eines Gegenbeispiels:

Wir betrachten die Vektoren $(\mathrm{1,0}{)}^T$ und $(\mathrm{0,1})T\in {ℝ}^2$. Wenn wir die beiden Vektoren zuerst addieren und danach abbilden, so erhalten wir

Nun bilden wir die Vektoren zuerst ab und addieren dann die Ergebnisse:

Also gilt

Damit ist gezeigt, dass die Normabbildung ist nicht additiv ist. Dies reicht schon aus um zu zeigen, dass die Normalabbildung nicht linear ist.

Alternativ hätten wir auch zeigen können, dass die Normalabbildung nicht homogen ist. Es gilt nämlich

Lineare Abbildungen werden in vielen Bereichen verwendet, ohne dass wir uns dessen bewusst sind:

1. Lineare Abbildungen sind eine der einfachsten Formen einer Abbildung. So werden komplexere Abbildungen häufig durch lineare Abbildungen approximiert.

2. Der bekannteste Fall, in dem uns lineare Abbildungen das Leben erleichtern, sind Computergrafiken. Jedes Skalieren eines Fotos oder einer Grafik ist eine lineare Abbildung. Auch verschiedene Bildschirmauflösungen wurden letztlich nur linear abgebildet.

3. Suchmaschinen nutzen Pageranks einer Website, um ihre Suchergebnisse zu sortieren. „Mathe für Nicht-Freaks“, eine zufällige Seite aus dem Internet, erhält so zum Beispiel ein Ranking. Um den Pagerank einer Seite zu bestimmen, wird eine sogenannte Markov-Kette verwendet, die wiederum eine lineare Abbildung ist.