1 Motivation
Lineare Abbildungen sind spezielle Abbildungen zwischen Vektorräumen, die sich gut mit der Vektorraumstruktur vertragen. Sie sind eines der wichtigsten Konzepte der linearen Algebra und haben zahlreiche Anwendungen.
Motivation
Die Besonderheit linearer Abbildungen
Wir haben die Struktur der Vektorräume kennengelernt und verschiedene Eigenschaften von ihnen untersucht. Nun wollen wir Vektorräume nicht nur isoliert voneinander betrachten, sondern auch Abbildungen zwischen ihnen. Manche dieser Abbildungen vetragen sich gut mit der zugrundeliegenden Vektorraumstruktur und werden deswegen lineare Abbildungen oder Vektorraumhomomorphismen genannt.
Dass wir solche strukturerhaltenden Abbildungen untersuchen, ist eine typische Vorgehensweise der Algebra. Für viele algebraische Strukturen wie Gruppen, Ringe oder Körper untersucht die Algebra die dazugehörigen strukturerhaltenden Abbildungen zwischen den jeweiligen algebraischen Strukturen – Gruppenhomomorphismen, Ringhomomorphismen und Körperhomomorphismus. Bei Vektorräumen sind die strukturerhaltenden Abbildungen die linearen Abbildungen bzw. die Vektorraumhomomorphismen.
Seien also und zwei Vektorräume. Wann ist eine Abbildung strukturerhaltend bzw. verträgt sich gut mit den zugrundeliegenden Vektorraumstrukturen in und ? Wiederholen wir hierzu, was die Vektorraumstruktur ausmacht: Vektorräume sind Strukturen, in denen zwei Operationen möglich sind:
Wiederholen wir hierzu, was die Vektorraumstruktur ausmacht: Vektorräume sind Strukturen, in denen zwei Operationen möglich sind:
Addition von Vektoren: Zwei Vektoren können miteinander addiert werden, wobei die Addition der Addition von Zahlen in ihren Eigenschaften ähnelt.
Skalare Multiplikation: Vektoren können mit einem Skalierungsfaktor aus einem Körper skaliert (gestaucht, gestreckt oder gespiegelt) werden.
Verträglichkeit der Addition
Beginnen wir mit der Addition von Vektoren: Wann verträgt sich eine Funktion mit den Additionen und auf den jeweiligen Vektorräumen und ? Hier kann man folgende Hypothese aufstellen:
Eine Abbildung ist verträglich mit der Addition, wenn eine Summe durch die Abbildung erhalten bleibt. Wenn also im Vektorraum eine Summe ist, so bilden auch die Bilder von , und im Vektorraum eine entsprechende Summe:
Eine mit der Addition verträgliche Abbildung erfüllt somit für alle die Implikation:
Diese Implikation kann in einer Gleichung zusammengefasst werden, indem die Prämisse in die zweite Gleichung eingsetzt wird. Es soll also für alle gelten:
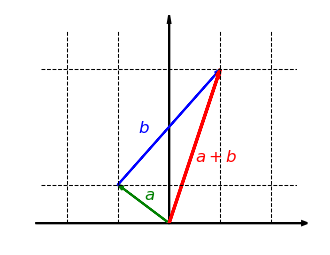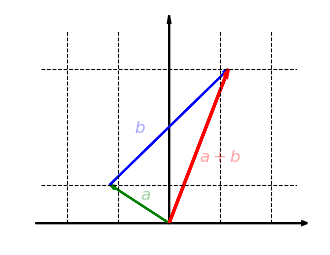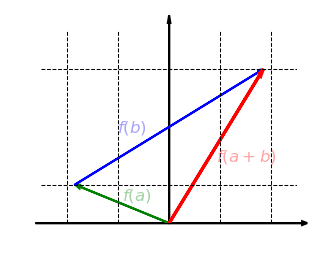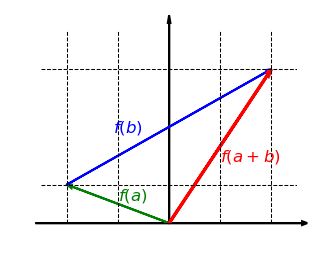
Diese Gleichung beschreibt die charakteristische Eigenschaft der linearen Abbildung, verträglich zur Vektoraddition zu sein. Wir können sie auch gut für Abbildungen visualisieren. Eine Abbildung verträgt sich genau dann mit der Addition, wenn das durch die Vektoren , und gegebene Dreieck im Definitionsbereich durch die Abbildung erhalten bleibt. Sprich: Auch die drei Vektoren , und bilden ein (Additions-)Dreieck:
Wenn sich nicht mit der Addition verträgt, gibt es Vektoren und mit . Das durch , und erzeugte Dreieck bleibt dann nicht erhalten, weil die Dreiecksseite des Ausgangsdreiecks nicht auf die Dreiecksseite des Zieldreiecks abgebildet wird:
Verträglichkeit mit der skalaren Multiplikation
Analog können wir uns überlegen, dass eine Abbildung genau dann verträglich mit der skalaren Multiplikation ist, wenn diese durch die Abbildung erhalten bleibt. Es sollte also für alle und für alle Skalare gelten:
Beachte, dass ein Skalar und kein Vektor ist und damit nicht durch die betrachtete Funktion veändert wird. Damit wir in der obigen Implikation denselben Skalar verwenden können, müssen beide Vektorräume denselben zugrundeliegenden Körper haben. Sowohl der Definitionsbereich als auch der Wertebereich muss ein -Vektorraum sein.
Lineare Abbildungen erhalten also Skalierungen. Aus folgt . Für den Fall, dass ist, werden Geraden der Form auf die Gerade abgebildet. Obige Implikation kann in eine Gleichung zusammengefasst werden. Es soll also für alle und gelten:
Für Abbildungen bedeutet dies, dass ein skalierter Vektoren auf die entsprechende Skalierung des Bildvektors abgebildet wird:
Wenn eine Abbildung nicht verträglich zur skalaren Multiplikation ist, so gibt es einen Vektor und einen Skalierungsfaktor , so dass ist:
2 Definition
Seien und Vektorräume über demselben Körper . Dabei seien und die jeweiligen inneren Verknüpfungen. Weiter seien und die skalaren Multiplikationen.
Nun sei eine Abbildung zwischen diesen Vektorräumen. Wir nennen eine lineare Abbildung von nach , wenn die folgenden beiden Eigenschaften erfüllt sind:
Additivität: Für alle gilt, dass
Homogenität: Für alle und gilt, dass
Wenn es aus dem Kontext klar ist, schreiben wir zukünftig auch einfach „“ anstatt und . Ebenso wird häufig „“ anstelle von und verwendet. Manchmal wird der Punkt für die skalare Multiplikation auch ganz weggelassen.
Hinweis
In der Literatur wird für den Begriff ''lineare Abbildung'' auch der Begriff ''Vektorraumhomomorphismus'' oder kurz ''Homomorphismus'' genutzt. Das altgriechische Wort homós steht für „gleich“, morphé steht für „Form“. Wörtlich übersetzt ist ein ''Vektorraumhomomorphismus'' also eine Abbildung zwischen Vektorräumen, welche die „Form“ der Vektorräume gleich lässt.
3 Erklärung zur Definition
Die charakteristischen Gleichungen der linearen Abbildung sind und . Was bedeuten diese beiden Eigenschaften intuitiv? Nach der Additivitätseigenschaft ist es egal, ob man und zuerst addiert und dann abbildet oder ob man beide Vektoren erst abbildet und dann addiert. Beide Wege führen zum selben Ergebnis:
Was besagt die Homogenitätseigenschaft? Unabhängig davon ob man zuerst mit multipliziert und dann abbildet oder den Vektor erst abbildet und dann mit multipliziert, ist das Ergebnis das Gleiche:
Die charakteristischen Eigenschaften der linearen Abbildungen verdeutlichen also, dass die Reihenfolge der Funktionsabbildung und der Vektorraumoperationen egal ist.
4 Charakterisierung: Linearkombinationen werden auf Linearkombinationen abgebildet
Neben der definierenden Eigenschaft, dass lineare Abbildungen sich gut mit der zugrundeliegenden Vektorraumstruktur vertragen, können lineare Abbildungen auch über folgende Eigenschaft charakterisiert werden:
Lineare Abbildungen sind genau die Abbildungen, die Linearkombinationen auf Linearkombinationen abbilden.
Dies ist eine wichtige Eigenschaft, weil über Linearkombinationen wichtige Struktureigenschaften von Vektoren wie die lineare Unabhängigkeit oder das Erzeugendensystemen definiert werden. Auch die Definition der Basis gründet sich auf den Begriff der Linearkombination. Den Zusammenhang zu den Linearkombinationen erkennt man, wenn man sich die beiden charakteristischen Gleichungen linearer Abbildungen anschaut:
Wir können auf eine Linearkombination wie für Vektoren und aus die beiden obigen Formeln schrittweise anwenden. So können wir diese Linearkombination aus der Funktion schrittweise „herausziehen“:
Die Linearkombination wird durch auf abgebildet und bleibt damit in ihrer Struktur erhalten. Ähnlich verhält es sich bei anderen Linearkombinationen. Denn durch die Eigenschaft sind Summen und durch die Eigenschaft sind skalare Multiplikationen herausziehbar. Wir erhalten damit folgende alternative Charakterisierung der linearen Abbildung:
Eine Abbildung zwischen zwei -Vektorräumen und ist genau dann eine lineare Abbildung, wenn sie Linearkombinationen erhält. Sprich: Jede lineare Abbildung bildet die Linearkombination von Elementen auf die Linearkombination von den Bildern der Elemente ab. Formal bedeutet das, dass für endlich viele und gilt:
Wir wollen zeigen, dass für alle und gilt:
Wir wissen aus der Definition der linearen Abbildung, dass für diese die Eigenschaften der Additivität und Homogenität gelten, welche wir uns zu Nutze machen.
Für die Richtung von links nach rechts des Beweises wählen wir 2 Linearkombinationen so, dass wir durch Einsetzen in die obige Formel die zwei Eigenschaften erhalten.
Für die Rückrichtung wissen wir, dass eine lineare Abbildung ist. Wir können durch vollständige Induktion zeigen, dass obige Formel für alle Elemente gilt. Dabei reduzieren wir die Linearkombination auf einzelne Additionen und Skalarmultiplikationen, auf die wir die Additivität und Homogenität anwenden können.
Beweisschritt:
Seien und . Die beiden Terme und sind zwei Linearkombinationen in . Wenn wir diese in die Formel einsetzen, so erhalten wir
Damit erfüllt die Definition einer linearen Abbildung.
Beweisschritt:
Sei eine lineare Abbildung. Wir beweisen die Gleichung mit vollständiger Induktion über :
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
1. Induktionsanfang:
Wir fangen die Induktion bei an und stellen fest, dass hierfür die Eigenschaft der Homogenität ausreicht:
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
2b. Induktionsbehauptung:
2c. Beweis des Induktionsschritts:
Seien und . Dann
5 Beispiele
Streckung in -Richtung
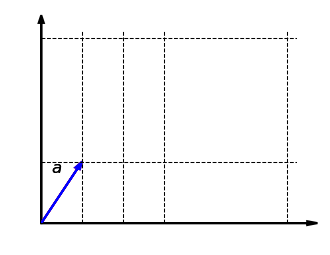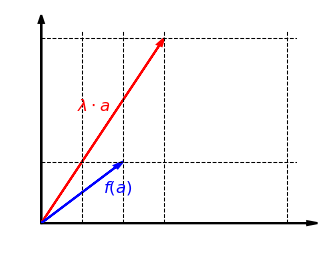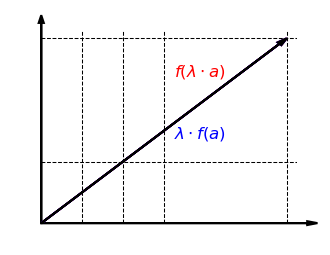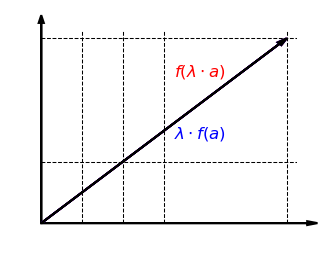
Unser erstes Beispiel ist die Streckung um den Faktor in -Richtung in der Ebene . Dabei wird jeder Vektor abgebildet auf . Die folgende Grafik zeigt diese Abbildung für . Die -Koordinate bleibt dabei gleich und die -Koordinate wird verdoppelt:
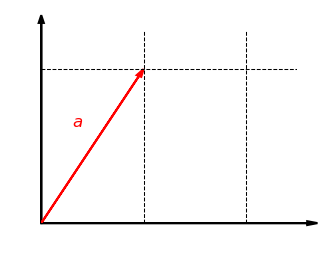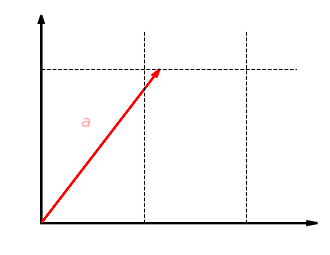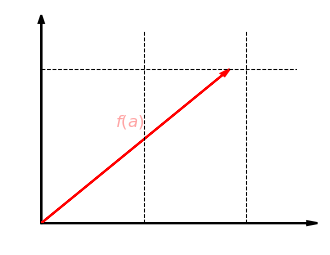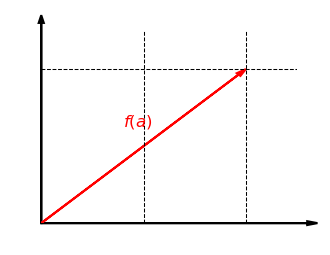
Schauen wir uns nun an, ob diese Abbildung verträglich mit der Addition ist. Nehmen wir also zwei Vektoren und , bilden die Summe und strecken diese dann in -Richtung. Das Ergebnis ist dasselbe, als wenn wir beide Vektoren zuerst in -Richtung strecken und dann addieren:
Das lässt sich auch mathematisch zeigen. Unsere Abbildung ist die Funktion
Wir können nun die Eigenschaft nachprüfen:
Schauen wir uns nun die Verträglichkeit mit der skalaren Multiplikation an. Die folgende Grafik zeigt, dass es egal ist, ob der Vektor zuerst mit einem Faktor skaliert und dann in -Richtung gestreckt wird oder zuerst in -Richtung gestreckt und dann mit skaliert wird:
Das lässt sich auch mathematisch zeigen. Unsere Abbildung ist die Funktion
Wir können nun die Eigenschaft nachprüfen:
Schauen wir uns nun die Verträglichkeit mit der skalaren Multiplikation an. Die folgende Grafik zeigt, dass es egal ist, ob der Vektor zuerst mit einem Faktor skaliert und dann in -Richtung gestreckt wird oder zuerst in -Richtung gestreckt und dann mit skaliert wird:

Auch das lässt sich formal zeigen: Für und gilt
Damit ist unser eine lineare Abbildung.
Drehungen
Im Folgenden betrachten wir eine Drehung der Ebene um den Winkel (gegen den Uhrzeigersinn gemessen) mit dem Ursprung als Drehzentrum. Es handelt sich dabei also um eine Abbildung , die jedem Vektor den um den Winkel gedrehten Vektor zuordnet:
Wir wollen uns jetzt davon überzeugen, dass eine lineare Abbildung ist. Dazu müssen wir zeigen:
ist additiv: Für alle ist .
ist homogen: Für alle und ist .
Überprüfen wir zunächst die Additivität, also die Gleichung . Addieren wir zwei Vektoren zuerst und drehen ihre Summe anschließend um den Winkel , so soll derselbe Vektor herauskommen, wie wenn wir erst die Vektoren um den Winkel drehen und im Anschluss die gedrehten Vektoren und addieren. Dies machen wir uns an folgenden beiden Videos klar:
Kommen wir nun zur Homogenität: . Strecken wir zunächst einen Vektor um einen Faktor und drehen das Resultat danach um den Winkel , so soll derselbe Vektor herauskommen, wie wenn wir als Erstes die Drehung um den Winkel durchführen und daraufhin das Ergebnis um den Faktor skalieren. Auch dies wird durch zwei Videos ersichtlich:
Somit handelt es sich bei Drehungen im um lineare Abbildungen.
Lineare Abbildung zwischen Vektorräumen unterschiedlicher Dimension
Ein Beispiel einer linearen Abbildung zwischen zwei Vektorräumen mit unterschiedlicher Dimension ist die folgende Projektion des Raums auf die Ebene :
Wir prüfen nun, ob die Vektoraddition erhalten bleibt. Also ob für Vektoren gilt
Dies können wir direkt nachweisen:
Nun überprüfen wir die Homogenität. Für alle und soll gelten:
Es ist
Damit ist die Projektion eine lineare Abbildung.
Eine nichtlineare Abbildung
Als nächstes untersuchen wir, ob es auch nicht lineare Abbildungen gibt. Hierzu betrachten wir die Normabbildung auf der Ebene, die jedem Vektor seine Länge zuordnet:
Diese Abbildung ist keine lineare Abbildung, denn sie erhält weder die Vektoraddition noch die Skalarmultiplikation.
Dies zeigen wir mit Hilfe eines Gegenbeispiels:
Wir betrachten die Vektoren und . Wenn wir die beiden Vektoren zuerst addieren und danach abbilden, so erhalten wir
Nun bilden wir die Vektoren zuerst ab und addieren dann die Ergebnisse:
Also gilt
Damit ist gezeigt, dass die Normabbildung ist nicht additiv ist. Dies reicht schon aus um zu zeigen, dass die Normalabbildung nicht linear ist.
Alternativ hätten wir auch zeigen können, dass die Normalabbildung nicht homogen ist. Es gilt nämlich
Angewandte Beispiele
Lineare Abbildungen werden in vielen Bereichen verwendet, ohne dass wir uns dessen bewusst sind:
Lineare Abbildungen sind eine der einfachsten Formen einer Abbildung. So werden komplexere Abbildungen häufig durch lineare Abbildungen approximiert.
Der bekannteste Fall, in dem uns lineare Abbildungen das Leben erleichtern, sind Computergrafiken. Jedes Skalieren eines Fotos oder einer Grafik ist eine lineare Abbildung. Auch verschiedene Bildschirmauflösungen wurden letztlich nur linear abgebildet.
Suchmaschinen nutzen Pageranks einer Website, um ihre Suchergebnisse zu sortieren. „Mathe für Nicht-Freaks“, eine zufällige Seite aus dem Internet, erhält so zum Beispiel ein Ranking. Um den Pagerank einer Seite zu bestimmen, wird eine sogenannte Markov-Kette verwendet, die wiederum eine lineare Abbildung ist.
6 Strukturerhaltung bei linearen Abbildungen
→ Hauptartikel: Eigenschaften Linearer Abbildungen
Eine lineare Abbildung bzw. ein Vektorraumhomomorphismus erhält die Struktur des Vektorraums beim Abbilden. Dies zeigt sich in folgenden Eigenschaften einer linearen Abbildung :
Nullvektor wird auf Nullvektor abgebildet:
Inverse werden auf Inverse abgebildet:
Linearkombinationen werden auf Linearkombinationen abgebildet
Kompositionen linearer Abbildungen sind linear
Bilder von Untervektorräumen sind Untervektorräume
Das Bild eines Spanns ist der Spann der einzelnen Bildvektoren: ( ist eine beliebige Menge)
7 Zusammenhang mit linearen Funktionen und affinen Abbildungen
Lineare Funktionen wurden in der Schule als Funktionen der Form mit eingeführt. Es handelt sich dabei nicht um lineare Abbildungen. Sie sind es nur für . So ist zum Beispiel für und :
Dass die in der Schule geläufigen linearen Funktionen dennoch etwas mit den linearen Abbildungen zu tun haben, wird einem klar, wenn man die linearen Abbildungen von betrachtet. Diese sind Abbildungen der Form mit . Die Funktionen der Form aus der Schule sind sogenannte affin-lineare Abbildungen: Sie sind die Summe einer linearen Abbildung und eines konstanten Terms .
Affine Abbildung bilden Geraden auf Geraden ab und erhalten dabei Parallelität und Teilverhältnisse von Strecken.
Wir können jede affine Abbildunge immer in eine lineare Abbildung und eine Translation zerlegen. Es gilt also . Weil die Translationen einfach zu beschreiben sind, ist der lineare Teil meistens interessanter. In der Theorie schauen wir uns deswegen nur den linearen Teil an, um nicht das mitzuschleppen.
8 Übungsaufgaben
Identität ist lineare Abbildung
Laden
Nullabbildung ist lineare Abbildung
Laden
Lineare Abbildungen zwischen den reellen Zahlen
Laden
