Welche der folgenden Dreiecke sind zueinander kongruent? Begründe deine Antwort mit einem passenden Kongruenzsatz.
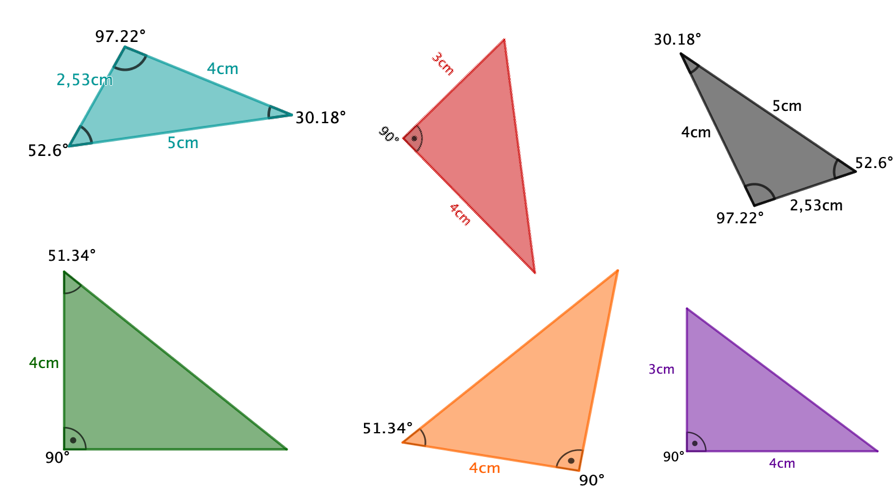
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruenz
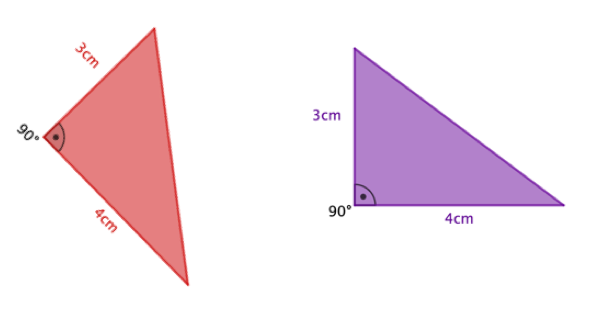
Um zu erkennen, dass das und das Dreieck kongruent sind, kannst du den SWS-Satz verwenden. Beide Dreiecke haben Seiten der Länge und und der von diesen Seiten eingeschlossene Winkel beträgt bei beiden .
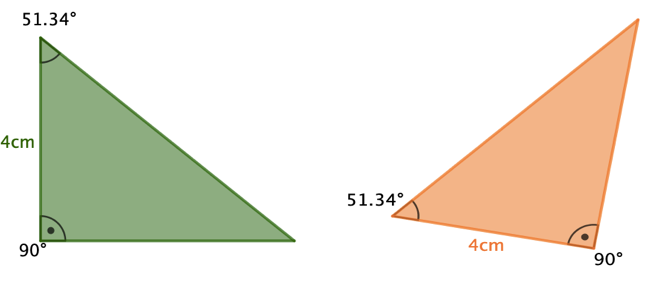
Das und Dreieck sind auch kongruent. Bei beiden Dreiecken hast du jeweils zwei Winkel und die dazwischenliegende Seitenlänge gegeben. Die Winkel und die Seitenlänge stimmen auch überein. Hier gilt also der WSW-Satz.
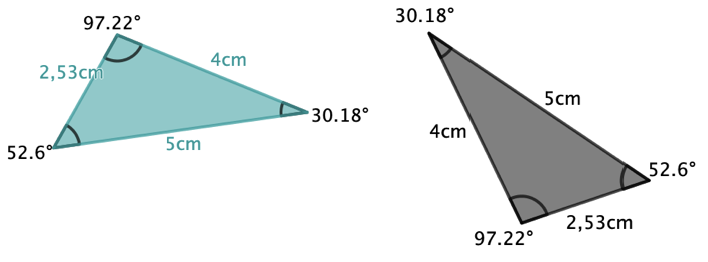
Beim und Dreieck hast du jeweils alle drei Seitenlängen gegeben. Weil diese alle miteinander übereinstimmen, kannst du mit dem SSS-Satz feststellen, dass sie kongruent sind.
Bei beiden Dreiecken hast du auch jeweils alle Winkel gegeben, du könntest statt dem SSS-Satz also auch einen beliebigen anderen Kongruenzsatz verwenden, um festzustellen, dass die Dreiecke kongruent sind.
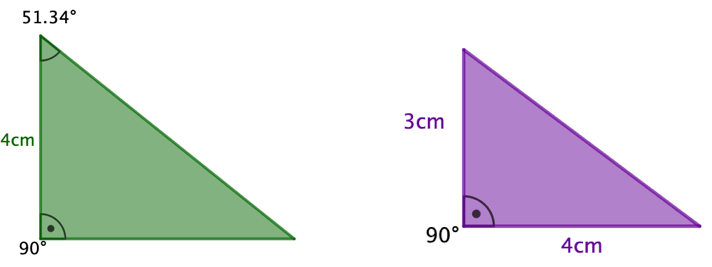
Das und Dreieck sind nicht kongruent. Da der größeren Seite auch der größere Winkel gegenüber liegt, ist beim Dreieck die Seite gegenüber dem Winkel länger als . Aber beim Dreieck hast du als Seitenlänge einmal und einmal gegeben. Somit stimmen die Seiten der beiden Dreiecke nicht überein und die Dreiecke sind nicht kongruent zueinander.
Wirf einen Blick auf die Kongruenzsätze und überlege dir für die einzelnen Dreiecke, welchen du verwenden könntest.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
