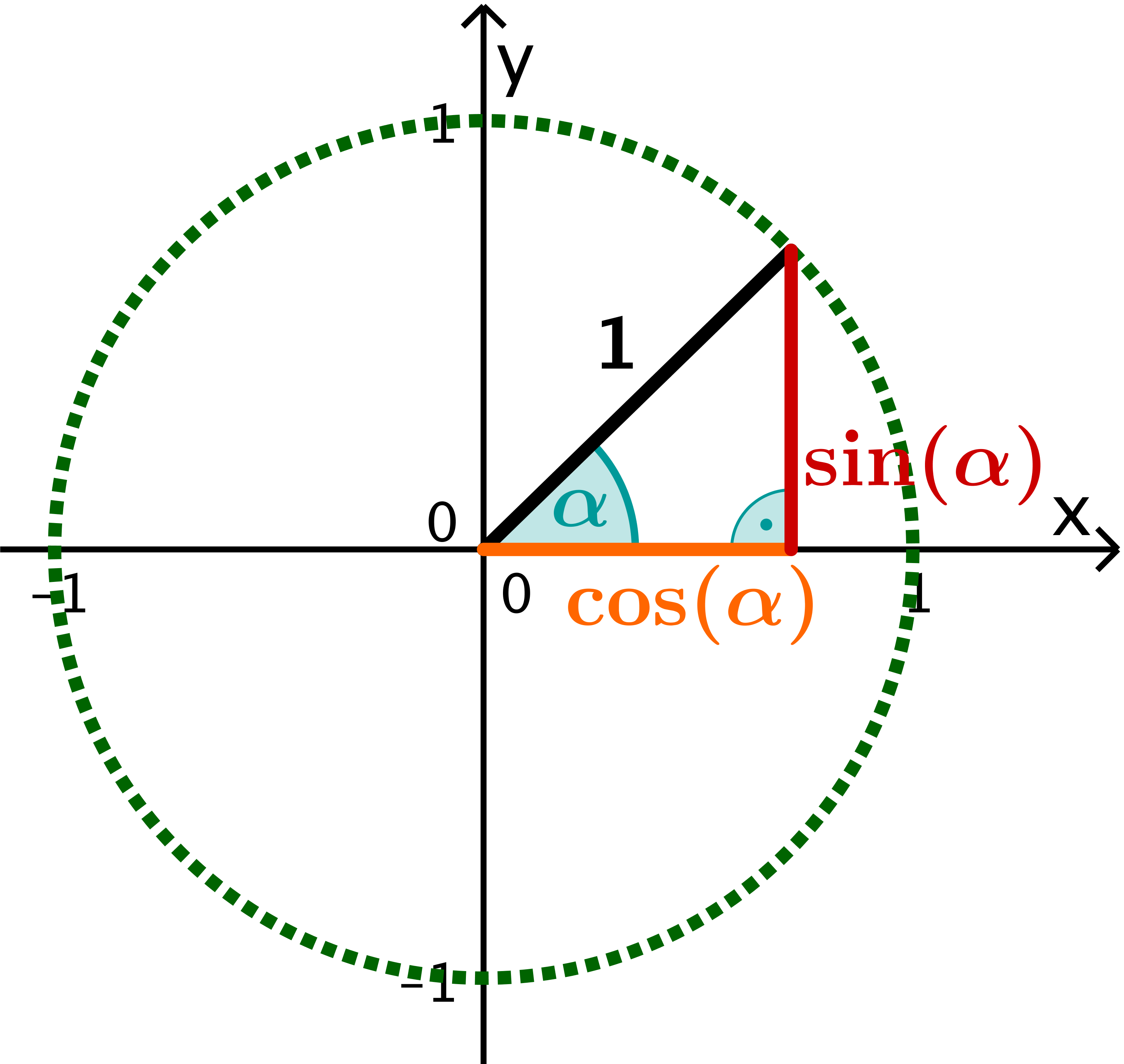
Trägt man an der -Achse einen Winkel an, kann man mithilfe des Einheitskreises die Werte des Sinus und Kosinus von ablesen.
Betrachtet man das rechtwinklige Dreieck mit Winkel im Einheitskreis, so hat die Hypotenuse die Länge :
Vorzeichen
Die trigonometrischen Funktionen können beim Übergang von einem Quadranten in den nächsten ihr Vorzeichen wechseln. Der Wechsel ist in folgenden Graphen veranschaulicht.
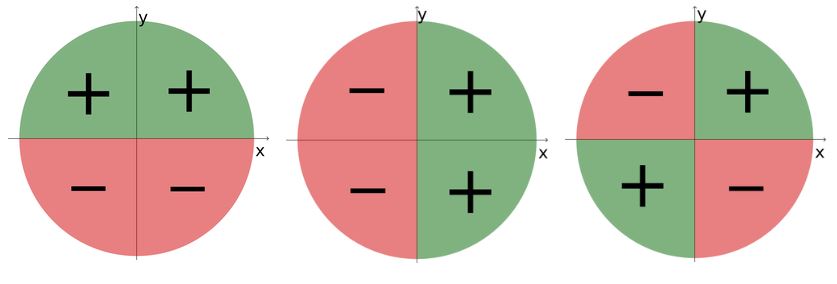
Sinus, Kosinus und Tangens - Vorzeichen der Funktionen in den Qudranten am Einheitskreis.
Wichtige Werte
In der unteren Tabelle sind einige wichtige Werte für die trigonometrischen Funktionen aufgeführt. Für die ersten fünf Werte des Sinus und Kosinus gibt es eine leichte Möglichkeit, sich die Werte zu merken. Sie haben die allgemeine Form , wobei man für den Sinus in aufsteigender Reihenfolge die Zahlen bis einsetzt und für den Kosinus in absteigender Reihenfolge.
Winkel | ||||||||
|---|---|---|---|---|---|---|---|---|
An diesen Stellen existiert der Tangens nicht, da der Tangens als "Sinus durch Kosinus" definiert ist und an diesen Stellen der Kosinus gleich null ist.
Veranschaulichung am Applet
Video zum Thema Tangens am Einheitskreis
Laden
Übungsaufgaben
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Sinus und Kosinus am Einheitskreis
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
