Bestimmung des Radius einer Kugel

Der Radius einer Kugel kann durch das Volumen oder die Oberfläche der Kugel berechnet werden.

Mit den Formeln

r = \sqrt[3]{\frac{3 V}{4 π}}

und

r = \sqrt{\frac{O}{4 π}}

kann der Radius (und damit auch der Durchmesser) bestimmt werden.

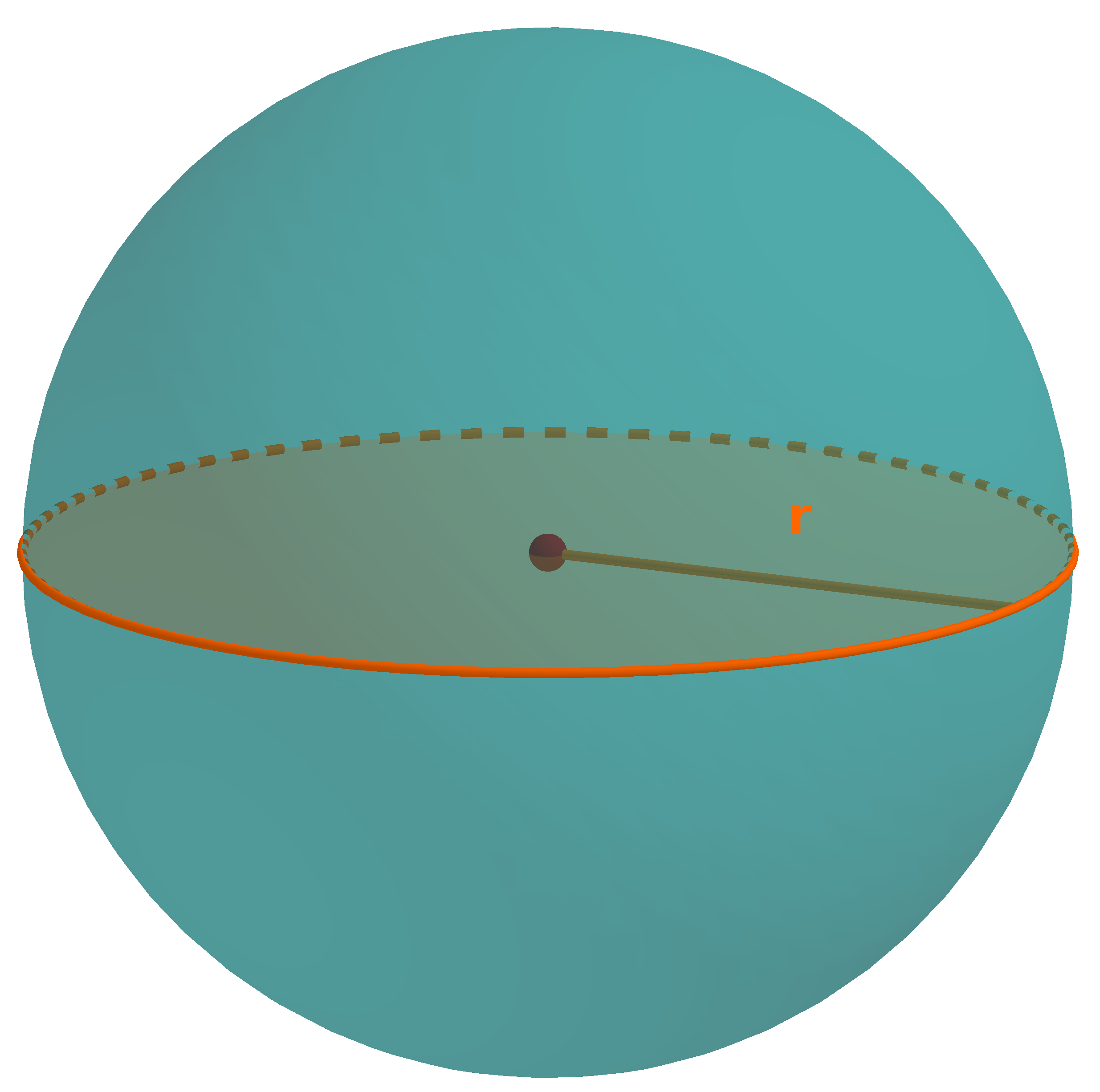
Hat man den Radius $r$ gegeben, berechnet man das Volumen mit der Formel

V = \frac{4}{3} π r^{3}

und die Oberfläche mit

O = 4 π r^{2} .

Ist der Radius unbekannt, aber das Volumen oder die Oberfläche gegeben, kann man diese Formeln umformen, um $r$ zu bestimmen.

Berechnung von $r$ bei gegebenem $V$

$V$	$=$	$\frac{4}{3} π r^{3}$	$: π$
	↓	Löse nach $r$ auf.
$\frac{V}{π}$	$=$	$\frac{4}{3} r^{3}$	$\cdot \frac{3}{4}$
	↓	Multipliziere mit dem Kehrbruch.
$\frac{V}{π} \cdot \frac{3}{4}$	$=$	$\frac{4}{3} \cdot \frac{3}{4} r^{3}$
	↓	Vereinfache. Durch Kürzen bekommst du $\frac{4}{3} \cdot \frac{3}{4} = 1$ .
$\frac{3 V}{4 π}$	$=$	$r^{3}$	$\sqrt[3]{}$
$r$	$=$	$\sqrt[3]{\frac{3 V}{4 π}}$

$O$	$=$	$4 π r^{2}$	$: 4 π$
	↓	Löse nach $r$ auf.
$r^{2}$	$=$	$\frac{O}{4 π}$	$\sqrt{}$
	↓	Ziehe die Wurzel. Da der Radius nicht negativ sein kann, gib nur die positive Lösung an.
$r$	$=$	$\sqrt{\frac{O}{4 π}}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?