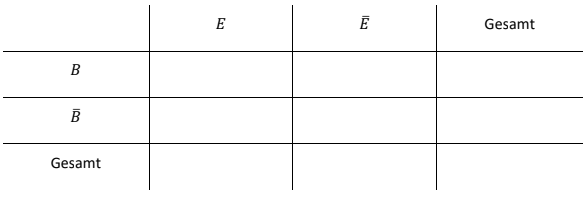
Der beschriebene Sachverhalt wird in einer Vierfeldertafel dargestellt. Dazu werden die folgenden Ereignisse betrachtet:

$B$ : Eine Person mit Pkw-Fahrerlaubnis kauft in Bioläden ein.

$E$ : Eine Person mit Pkw-Fahrerlaubnis interessiert sich für den Kauf eines Elektroautos.

Füllen Sie die Vierfeldertafel vollständig aus. (3BE)

Beurteilen Sie die Gültigkeit der folgenden Aussage: (2BE)

In der betrachteten Gruppe interessieren sich unter denjenigen, die in Bioläden einkaufen, mehr als die Hälfte für den Kauf eines Elektroautos.

Aus der betrachteten Gruppe werden 30 Personen zufällig ausgewählt.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass mindestens zwei Drittel der ausgewählten Personen am Kauf eines Elektroautos nicht interessiert sind. (3BE)

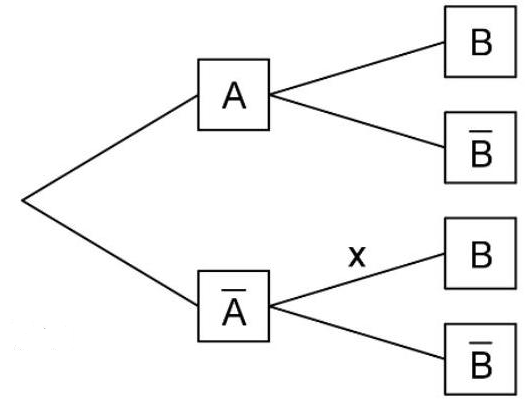
Ermitteln Sie den im Baumdiagramm genannten Anteil $x$.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Elektroauto des Herstellers das Merkmal B aufweist. (4BE)

Beschreiben Sie im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term $1-10 \cdot 0{,}3 \cdot 0{,}7^{9}-0{,}7^{10}$ berechnet werden kann.

Geben Sie dieses Ereignis an. (3BE)

Zehn Elektroautos des Herstellers werden nacheinander betrachtet.

Ermitteln Sie, wie viele Autos mit dem Merkmal A sich unter diesen zehn Autos mindestens befinden müssen, damit mit einer Wahrscheinlichkeit von mindestens $90 \%$ von den ersten drei betrachteten Autos mindestens eines das Merkmal A aufweist. (4BE)