Abiturprüfungen Mathe gA mit Lösungen

Aufgabe 1A

Ein Unternehmen verkauft Fitnessarmbänder.

Die momentane Änderungsrate des Absatzes wird beschrieben mit der in $\mathbb{R}$ definierten Funktion $f$ mit:

$f(x)=4000 \cdot x \cdot e^{-0{,}4 \cdot x} ; 0 \leq x \leq 18$

Dabei ist $x$ die seit der Produkteinführung vergangene Zeit in Monaten und $f(x)$ die momentane Änderungsrate des Absatzes in Stück pro Monat.

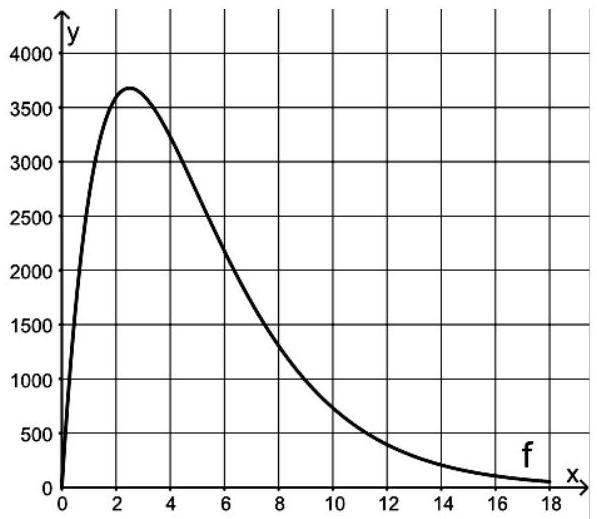
Berechnen Sie den Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht, und geben Sie diesen größten Wert an.
Kennzeichnen Sie in der Abbildung diejenigen Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören. (6BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht
Löse die Gleichung $f'(x)=0$ . Du erhältst als einzige Lösung $x=2{,}5$ .
Der Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht, ist $x=2{,}5$ Monate.
Größter Wert
Berechne $f(2{,}5)=4000 \cdot 2{,}5 \cdot e^{-0{,}4 \cdot 2{,}5} =\dfrac{10000}{e}\approx3679$
Die momentane Änderungsrate des Absatzes hat $2{,}5$ Monate nach Produkteinführung den größten Wert von $3679$ Stück pro Monat.
Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören
Graph der Funktion $f$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Löse $f'(x)=0$ .
Teil 2
Berechne $f(2{,}5)$ .
Teil 3
Zeichne $y=1000$ in die Abbildung ein und kennzeichne die Schnittpunkte mit $f(x)$ .
Im Beobachtungszeitraum gibt es einen Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes am stärksten zunimmt, und einen Zeitpunkt, zu dem sie am stärksten abnimmt. Zur Bestimmung dieser beiden Zeitpunkte wurden folgende Berechnungen durchgeführt:
i. $\quad f^{\prime \prime}(x)=0 \Leftrightarrow x=5$
ii. $\quad f^{\prime \prime \prime}(5)>0$
Erläutern Sie diese beiden Berechnungen.
Bestimmen Sie ohne weitere Rechnung die beiden gesuchten Zeitpunkte. (6BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Erläuterung zu den Berechnungen
$f'$ beschreibt die Zu- und Abnahme der momentanen Änderungsrate des Absatzes.
Die möglichen Extremstellen von $f'$ sind die Nullstellen von $f''$ .
Nach Gleichung $\mathrm{i:}\quad f^{\prime \prime}(x)=0 \Leftrightarrow x=5$ und Gleichung $\mathrm{ii:}\quad f'''(x)>5$ gilt, dass $f'$ an der Stelle $x=5$ ein Minimum hat.
Die beiden Zeitpunkte
Der Graph von $f$ zeigt, dass $f'(0)>0$ und $f'(18)<0$ ist.
Da es im Inneren des Definitionsbereiches kein Maximum geben kann, nimmt $f'$ sein Maximum an der Stelle $x=0$ an.
Die momentane Änderungsrate des Absatzes nimmt also zum Zeitpunkt der
Produkteinführung am stärksten zu und fünf Monate danach am stärksten ab.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f'$ beschreibt die Zu- und Abnahme der momentanen Änderungsrate des Absatzes.
Die möglichen Extremstellen von $f'$ sind die Nullstellen von $f''$ .
Gleichzeitig mit der Einführung des Fitnessarmbands brachte das Unternehmen eine Smartwatch auf den Markt. Die momentane Änderungsrate des Absatzes der Smartwatch in Stück pro Monat wird mithilfe der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=1600 \cdot x^{2} \cdot e^{-0{,}4 \cdot x}$ beschrieben. Dabei ist $x$ die seit der Produkteinführung vergangene Zeit in Monaten und $g(x)$ die momentane Änderungsrate des Absatzes in Stück pro Monat.
Vergleichen Sie die momentanen Änderungsraten des Absatzes für das Fitnessarmband und die Smartwatch fünf Monate nach Produkteinführung. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Vergleich der momentanen Änderungsraten
Berechne $f(5)$ und $g(5)$ und vergleiche die Werte.
$f(5)\approx2707$ und $g(5) \approx5413$ $\;\Rightarrow\;g(5)\approx2\cdot f(5)$
Fünf Monate nach Produkteinführung ist die momentane Änderungsrate des
Absatzes für die Smartwatch etwa doppelt so groß wie die für das Armband.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $f(5)$ und $g(5)$ und vergleiche die Werte.
Berechnen Sie die Anzahl der im ersten Jahr nach Produkteinführung insgesamt verkauften Smartwatches.
Untersuchen Sie, ob es einen Zeitpunkt nach Produkteinführung gibt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden.
Geben Sie gegebenenfalls diesen Zeitpunkt an. (6BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
Anzahl der im ersten Jahr verkauften Smartwatches
Berechne das Integral von $0$ bis $12$ (Monate) über $g(x)$ :
$\displaystyle\int_0^{12}g(x)\;dx\approx42873$
Die Anzahl der im ersten Jahr nach Produkteinführung insgesamt verkauften Smartwatches beträgt rund $42900$ .
Zeitpunkt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden
Es muss für den Zeitraum $t$ gelten:
$\displaystyle\int_0^{t}f(x)\;dx=\displaystyle\int_0^{t}g(x)\;dx$
Eine Lösung ist $t=0$ .
Die zweite Lösung findet man, indem die Graphen der Stammfunktionen von $f$ und $g$ gezeichnet werden und der Schnittpunkt bestimmt wird.
Zeichne $\displaystyle\int_0^{t}f(x)\;dx$ und $\displaystyle\int_0^{t}g(x)\;dx$ . Bestimme die Schnittpunkte.
Der zweite Schnittpunkt liegt bei $x\approx 4{,}4832...$ .
Nach etwa $4{,}5$ Monaten wurden ebenso viele Fitnessarmbänder wie Smartwatches verkauft.
Beachte
Für die Berechnung des zweiten Schnittpunktes brauchte der CASIO fx-CG 20 rund 2,5 Minuten!
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne das Integral von $0$ bis $12$ (Monate) über $g(x)$ .
Teil 2
Zeichne $\displaystyle\int_0^{t}f(x)\;dx$ und $\displaystyle\int_0^{t}g(x)\;dx$ . Bestimme die Schnittpunkte.
Gegeben sind nun die in $\mathbb{R}$ definierten Funktionen $h_{b}$ mit $h_{b}(x)=x \cdot e^{-0{,}1 \cdot b \cdot x} ; b>0$ .
Für jeden Wert von $b$ ist $E\left(\frac{10}{b}\left\lceil\frac{10}{b} \cdot e^{-1}\right)\right.$ der Extrempunkt und $W\left(\frac{20}{b} \left\lvert\, \frac{20}{b} \cdot e^{-2}\right.\right)$ der
Wendepunkt des Graphen von $h_{b}$ .
Betrachtet wird zunächst $h_{1}$ . Die
nebenstehende Abbildung zeigt den Graphen von $h_{1}$ .
Geben Sie für den Graphen von $h_{1}$ die Koordinaten des Extrempunktes und des Wendepunktes an. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Koordinaten des Extrempunktes und des Wendepunktes
Es ist $E\left(\frac{10}{b} \mid\frac{10}{b} \cdot e^{-1}\right)$ und $W\left(\frac{20}{b} \mid \frac{20}{b} \cdot e^{-2}\right)$ mit $b=1$ folgt dann:
$E\left(10 \mid10 \cdot e^{-1}\right)$ und $W\left(20 \mid 20 \cdot e^{-2}\right)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Setze $b=1$ in $E$ und $W$ ein.
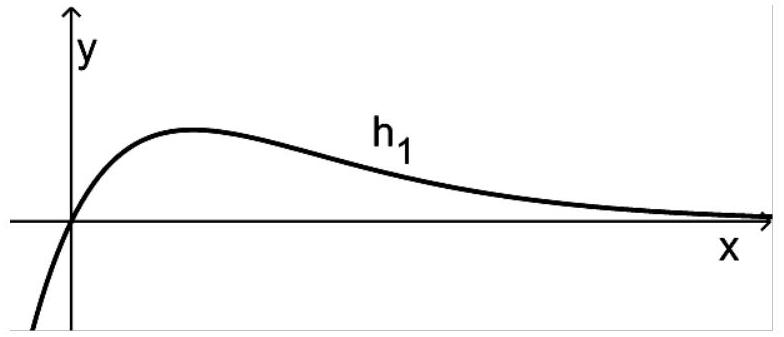
Die Tangente an den Graphen von $h_{1}$ in dessen Wendepunkt und der Graph von $h_{1}$ schließen mit der $x$ -Achse eine Fläche ein.
Bestimmen Sie deren Flächeninhalt. (6BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Tangentengleichung aufstellen
Bestimme die Tangentengleichung durch den Wendepunkt $W\left(20 \mid 20 \cdot e^{-2}\right)$ .
Dazu wird die Steigung im Wendepunkt benötigt:
Lasse Dir die Steigung der Funktion $h_1$ an der Stelle $x=20$ anzeigen:
Es ist $\dfrac{d}{dx}(h_1(x))|_{x=20}\approx -0{,}135335...$ . Also ist $m\approx-0{,}135$ .
Für die Tangentengleichung folgt dann:
Setze die Koordinaten des Wendepunktes ein:
Damit lautet die Tangentengleichung:
Nullstelle der Tangente und Integrationsgrenze für später
Berechne die Nullstelle der Tangente: $-0{,}135\cdot x+5{,}41=0\;\Rightarrow\;x_N\approx40$
Flächeninhalte bestimmen
Nun kann der gesuchte Flächeninhalt berechnet werden.
Für das Integral folgt: $\displaystyle\int_0^{20}h_1(x)\;dx\approx59{,}399415...$
Für die Dreiecksfläche gilt: $A=\dfrac{1}{2}\cdot g \cdot h$
Mit $g=40-20=20$ und $h=h_1(20)=\dfrac{20}{e^2}\;\Rightarrow\;A_\triangle=\dfrac{1}{2}\cdot 20\cdot\dfrac{20}{e^2}=\dfrac{200}{e^2}\approx27{,}067$
Damit ergibt sich der gesuchte Flächeninhalt zu:
Die Tangente an den Graphen von $h_{1}$ in dessen Wendepunkt und der Graph von $h_{1}$ schließen mit der $x$ -Achse eine Fläche von rund $86{,}5\; \text{FE}$ ein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bestimme die Tangentengleichung durch den Wendepunkt.
Berechne die Nullstelle der Tangente.
Der gesuchte Flächeninhalt ist dann: $A=\displaystyle\int_0^{20}h_1(x)\;dx+A_\triangle$
Jeder Punkt $E$ liegt auf einer Ursprungsgeraden und jeder Punkt $W$ liegt auf einer anderen Ursprungsgeraden.
Geben Sie die Gleichungen dieser beiden Ursprungsgeraden an. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortskurve bestimmen
Gleichungen der beiden Ursprungsgeraden
Es ist $E\left(\frac{10}{b} \mid\frac{10}{b} \cdot e^{-1}\right)$
$x=\dfrac{10}{b}\;\Rightarrow\;b=\dfrac{10}{x}$
Für y eingesetzt ergibt sich die Geradengleichung:
$y=\frac{10}{b} \cdot e^{-1}$
Setze $b=\dfrac{10}{x}$ in $y$ ein $\;\Rightarrow\;y=\dfrac{10}{\dfrac{10}{x}}\cdot e^{-1} =\dfrac{1}{e}\cdot x$
Die Gerade, auf der die Extrempunkte liegen, ist: $y=\dfrac{1}{e}\cdot x$ .
Es ist $W\left(\frac{20}{b} \mid \frac{20}{b} \cdot e^{-2}\right)$
$x=\dfrac{20}{b}\;\Rightarrow\;b=\dfrac{20}{x}$
Für $y$ eingesetzt ergibt sich die Geradengleichung:
$y=\frac{20}{b} \cdot e^{-2}$
Setze $b=\dfrac{20}{x}$ in $y$ ein $\;\Rightarrow\;y=\dfrac{20}{\dfrac{20}{x}}\cdot e^{-2} =\dfrac{1}{e^2}\cdot x$
Die Gerade, auf der die Wendepunkte liegen, ist: $y=\dfrac{1}{e^2}\cdot x$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für den Extrempunkt gilt: $x=\dfrac{10}{b}$ . Löse nach $b$ auf und setze in $y=\frac{10}{b} \cdot e^{-1}$ ein.
Für den Wendepunkt gilt: $x=\dfrac{20}{b}$ . Löse nach $b$ auf und setze in $y=\frac{20}{b} \cdot e^{-2}$ ein.
$O$ bezeichnet den Koordinatenursprung.
Beurteilen Sie die Gültigkeit der folgenden Aussage: (4BE)
Alle Dreiecke $O W E$ sind ähnlich.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kongruente und ähnliche Dreiecke
Begründung
Betrachte zunächst das Dreieck für $b=1$ mit den Koordinaten $O(0|0), E_1(10|\frac{10}{e})$ und $W_1(20|\frac{20}{e^2})$ . Betrachte nun ein Dreieck für beliebiges $b$ . Es hat die Koordinaten $O(0|0), E_b(\frac{10}{b}|\frac{10}{b\cdot e})$ und $W_b(\frac{20}{b}|\frac{20}{b\cdot e^2})$ .
Für beliebige Werte von $b$ geht das Dreieck $OWE$ aus dem entsprechenden
Dreieck für $b=1$ durch Streckung mit dem Faktor $\dfrac{1}{b}$ hervor, wobei das Streckzentrum im Koordinatenursprung liegt.
Daher sind alle Dreiecke $OWE$ ähnlich.
Visualisierung
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung. Gezeichnet sind die Dreiecke für $b=1$ und $b=2$ .
Zwei ähnliche Dreiecke
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für beliebiges $b$ entsteht das Dreieck $OWE$ aus dem Dreieck für $b=1$ durch Streckung mit dem Faktor $\dfrac{1}{b}$ . Das Streckzentrum ist der Ursprung.

2

Aufgabe 1B

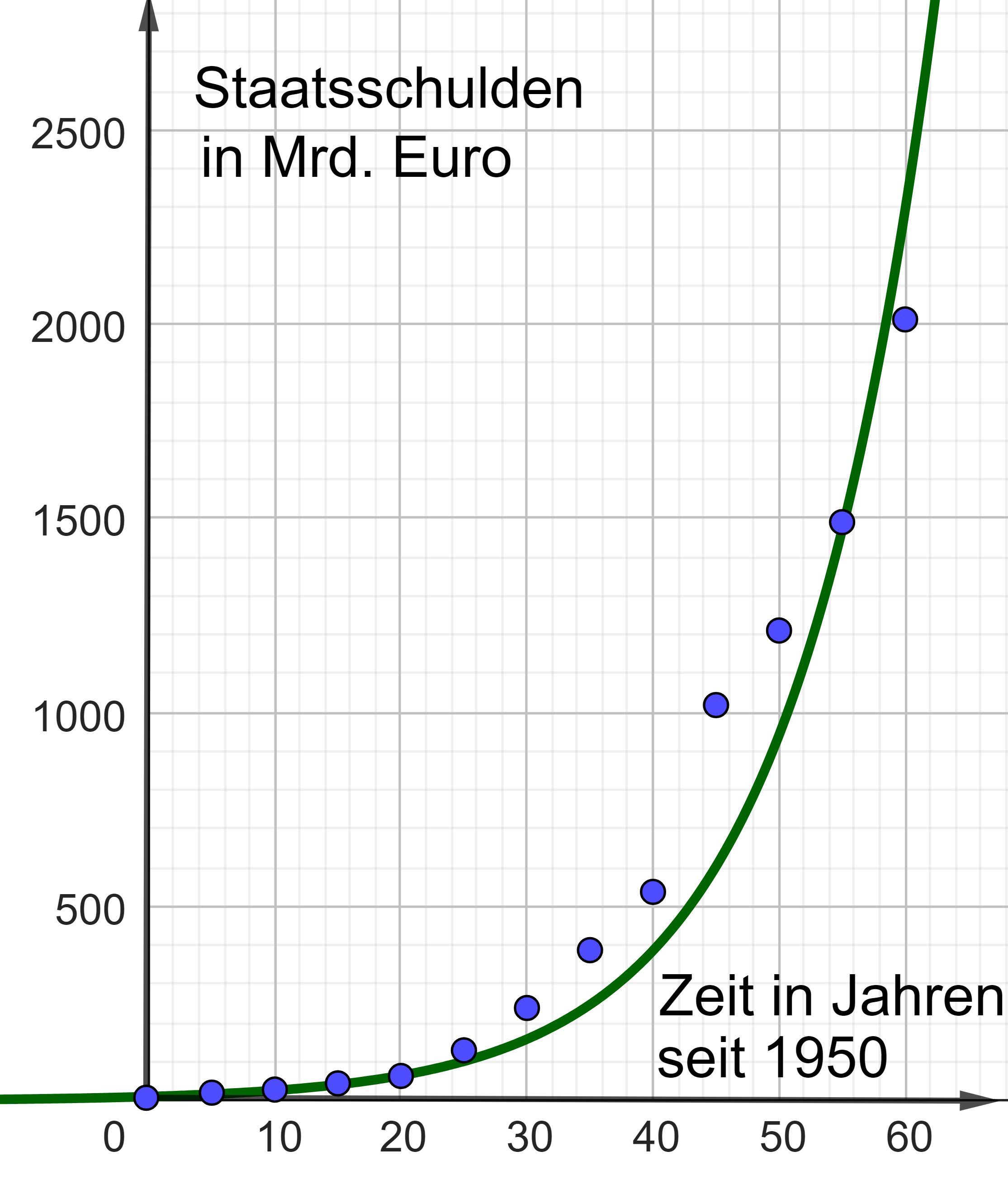
Die Grafik zeigt die Schulden Deutschlands zu Beginn eines Jahres für die Jahre $1950$ bis $2010$ in Mrd. Euro.

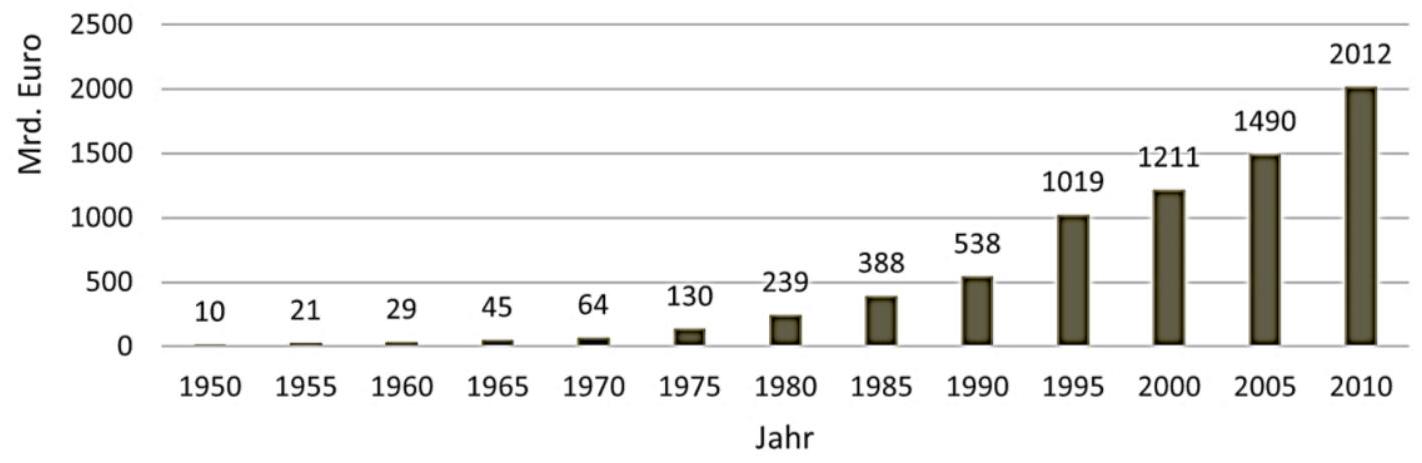
Geben Sie die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Diagramme erfassen und auswerten
Die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben
Dem Diagramm entnimmt man die erste Jahreszahl $1950$ mit $10$ Milliarden €.
$1955$ hat sich der Schuldenstand auf $21$ Milliarden € erhöht, also etwas mehr als verdoppelt.
Im weiteren Verlauf findet man dann das Jahr $1970$ mit $64$ Milliarden € und nach $5$ Jahren, also $1975$ einen Schuldenstand von $130$ Milliarden €, also etwas mehr als verdoppelt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte benachbarte Datensätze, bei denen einer etwa doppelt so groß wie der vorherige ist.
Geben Sie ein Verfahren an zur Bestimmung einer Funktion, die für den Zeitraum von $1950$ bis $2010$ die Schulden in Abhängigkeit von der Zeitdauer seit $1950$ näherungsweise beschreibt.
Nennen Sie drei Schritte der Durchführung des Verfahrens. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steckbriefaufgaben
Verfahren zur Bestimmung einer Funktion
Eines der beiden Verfahren sollte genannt werden:
Parameterbestimmung oder Regression
Drei Schritte der Durchführung des Verfahrens
1. Parameterbestimmung:
Auswahl des Funktionstyps
Auswahl geeigneter Wertepaare
Lösen des Gleichungssystems
2. Regression:
Auswahl des Funktionstyps
Eingabe aller Wertepaare in den Taschenrechner
Bestimmung des Funktionsterms
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Eines der beiden Verfahren sollte genannt werden; Parameterbestimmung oder die Regression.
Gib jeweils drei Schritte an, wie das Verfahren abläuft.
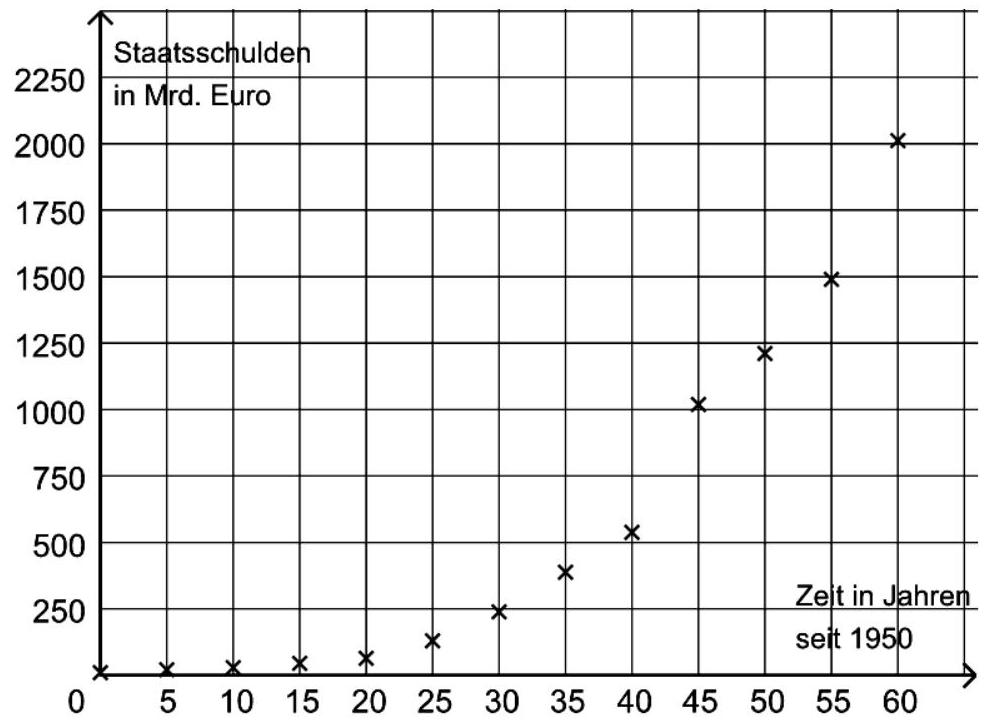
In der nebenstehenden Abbildung sind die Daten aus der Grafik eingetragen.
Die auf ganz $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=11 \cdot e^{0{,}089 x}$ beschreibt für $0 \leq x \leq 60$ näherungsweise die Schulden Deutschlands von $1950$ bis $2010$ . Dabei gibt $x$ die Zeit in Jahren seit $1950$ an und $f(x)$ die Schulden in Mrd. Euro.

Zeichnen Sie den Graphen von $f$ in die Abbildung. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Zeichnung des Graphen von $f$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle eine Wertetabelle für die Funktion $f$ , trage die Werte in die Abbildung ein und verbinde die Punkte.
Bestimmen Sie mithilfe der Funktion $f$ die jährliche prozentuale Zunahme der Schulden.
Untersuchen Sie, ob es einen Zeitpunkt gibt, zu dem die momentane Änderungsrate der Schulden größer als $250$ Mrd. Euro pro Jahr ist. (5BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Jährliche prozentuale Zunahme der Schulden
Es ist $f(x)=11 \cdot e^{0{,}089 x}\;\Rightarrow\;e^{0{,}089 }\approx1{,}093$ .
Damit beträgt die jährliche prozentuale Zunahme der Schulden etwa $9{,}3\;\%$ .
Zeitpunkt, zu dem die momentane Änderungsrate der Schulden größer als $250$ Mrd. Euro pro Jahr ist
Die Funktion $f$ beschreibt ein exponentielles Wachstum.
Die erste Ableitung von $f$ erreicht ihr Maximum am rechten Rand des Definitionsbereiches. d.h. für $x=60$ :
$f'(60)=11\cdot 0{,}089 \cdot e^{0{,}089 \cdot 60}\approx 204<250$
Somit gibt es keinen Zeitpunkt, an dem die momentane Änderungsrate der Schulden größer als $250$ Mrd. Euro ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne $e^{0{,}089}$ .
Teil 2
Berechne $f'(60)$ und vergleiche mit $250$ .
Im Folgenden wird in einem anderen Modell die momentane Änderungsrate der Schulden Deutschlands zu Beginn eines Jahres ab dem Jahr 2005 betrachtet. Sie wird für $x \geq 0$ durch die auf ganz $\mathbb{R}$ definierte Funktion $g$ mit $g(x)=250 \cdot e^{-0{,}25 x}-38$ beschrieben.
Dabei gibt $x$ die Zeit in Jahren seit 2005 und $g(x)$ die momentane Änderungsrate der Schulden in Mrd. Euro pro Jahr an.
Ohne Nachweis können Sie verwenden, dass $G$ mit $G(x)=-1000 \cdot e^{-0{,}25 x}-38 \cdot x$ eine Stammfunktion von $g$ ist.
Begründen Sie, dass in der Modellierung mit $g$ die momentane Änderungsrate der Schulden ab Beginn des Jahres $2005$ abnimmt.
Berechnen Sie das Jahr, in dem die Schulden ihren Höchststand erreichen. (6BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentielles Wachstum
Das Jahr, in dem die Schulden ihren Höchststand erreichen
Gegeben ist $g(x)=250 \cdot e^{-0{,}25 x}-38$ .
Es sind $250 > 0$ und $e^ {−0{,}25} < 1$ .
Dann beschreibt der Term $250 \cdot e^{−0{,}25}$ eine exponentielle Abnahme, weil die Basis kleiner als 1 ist und der Graph nicht gespiegelt ist. Die Funktion $g$ ist also monoton fallend.
Berechne $g(x)=0$ :
Der GTR liefert die Lösung $x_1$ mit $x_1\approx7{,}535499033$ $\;\Rightarrow\;x_1\approx7{,}54$ .
$\Rightarrow\;2005+7{,}54\approx2012$
Der Höchststand der Schulden besteht im Verlauf des Jahres $2012$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Untersuche das Monotonieverhalten der Funktion $g$ .
Berechne $g(x)=0$ .
Im Folgenden werden die zu erwartenden Schulden Deutschlands $m$ Jahre nach dem Jahr 2005 für $0 \leq m \leq 70$ betrachtet.
Begründen Sie, dass sich die zu erwartenden Schulden zu Beginn des Jahres $2005+m$ mithilfe des folgenden Terms berechnen lassen: $1490+\displaystyle\int_{0}^{m} g(x)\; d x$
Bestimmen Sie das Jahr, in dem die Schulden vollständig abgebaut sind. (7BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Integrale
Begründung, dass sich die zu erwartenden Schulden zu Beginn des Jahres $2005+m$ mithilfe des folgenden Terms berechnen lassen: $1490+\displaystyle\int_{0}^{m} g(x)\; d x$
Es ist $\displaystyle\int_{0}^{m} g(x)\; d x$ . Dabei gibt die Funktion $𝑔$ die Änderung des Schuldenstandes ab $2005$ in Milliarden € pro Jahr an. Mit diesem Integral lassen sich die seit Beginn des Jahres $2005$ im Zeitraum von $m$ Jahren insgesamt hinzugekommenen Schulden berechnen.
$1490$ Milliarden € ist der Schuldenstand zu Beginn des Jahres $2005$ . Zusammen mit dem Integral erhält man die Schulden im Jahr $2005+m$ .
Das Jahr, in dem die Schulden vollständig abgebaut sind
Berechne $1490+\displaystyle\int_{0}^{m} g(x)\; d x=0$ :
Der GTR liefert als positive Lösung $m\approx65{,}526313...$ .
$m\approx65{,}5\;\Rightarrow\;2005+65{,}5\approx2070$
Im Verlauf des Jahres 2070 sind die Schulden vollständig abgebaut.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $1490+\displaystyle\int_{0}^{m} g(x)\; d x=0$
Begründen Sie, dass die Lösungen der Gleichung $\dfrac{g(m)}{1490+\displaystyle\int_{0}^{m} g(x) d x}=0{,}05$ Zeitpunkte nach dem Jahr $2005$ angeben, zu denen die Schulden um $5 \%$ der vorhandenen Schulden wachsen.
Bestimmen Sie den Zeitraum, in dem die momentane Änderungsrate der Schulden weniger als $5 \%$ der Schulden beträgt. (8BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung
Zeitraum bestimmen
Der Quotient auf der linken Seite beschreibt den Anteil der momentanen Änderungsrate der Schulden im Jahr $m$ nach $2005$ an den Schulden im Jahr $2005+m$ .
Damit sind die Lösungen der Gleichung die Zeitpunkte nach dem Jahr $2005$ , zu denen dieser Anteil $5\;\%$ beträgt.
Für die Zeit zwischen den beiden Zeitpunkten beträgt die momentane Änderungsrate der Schulden weniger als $5 \%$ der Schulden.
Löse die Gleichung $\dfrac{g(m)}{1490+\displaystyle\int_{0}^{m} g(x) d x}=0{,}05$ :
Der GTR liefert im betrachteten Zeitraum $0 \leq m \leq 70$ die Lösung $m_1$ mit $m_1\approx2{,}57468358$ $\;\Rightarrow\;m_1\approx2{,}6$ .
Nun ist aber für $m<m_1$ , also z.B. für $m=2{,}5$ der Term $\dfrac{g(2{,}5)}{1490+\displaystyle\int_{0}^{2{,}5} g(x) d x} \approx 0{,}05152087>0{,}05$
Demnach ist $2005 + m_1$ der Anfang des gesuchten Zeitraums etwa das Jahr $2007$ .
In Aufgabe e) wurde gezeigt, dass $g(7{,}54)\approx0$ ist. Für $x>7{,}54$ ist dann $g(x)<0$ .
Somit kann auch der Quotient negativ werden.
Löse die Gleichung $\dfrac{g(m)}{1490+\displaystyle\int_{0}^{m} g(x) d x}=-0{,}05$ :
Der GTR liefert im betrachteten Zeitraum $0 \leq m \leq 70$ die Lösung $m_2$ mit $m_2\approx45{,}52751581$ .
Es ist also $m_2\approx 45{,}5$ und das Ende des gesuchten Zeitraums ist etwa 2050.
Der gesuchte Zeitraum beginnt im Jahr $2007$ und endet im Jahr $2050$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse die beiden Gleichungen:
$\dfrac{g(m)}{1490+\displaystyle\int_{0}^{m} g(x) d x} = 0{,}05$ und $\dfrac{g(m)}{1490+\displaystyle\int_{0}^{m} g(x) d x} = -0{,}05$
Du erhältst zwei Werte für $m$ , die im Bereich $0 \leq m \leq 70$ liegen müssen.

3

Aufgabe 1C

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=-\frac{1}{640} x^{4}+\frac{1}{40} x^{3}-\frac{9}{80} x^{2}+\frac{1}{5} x+3$ .

Ohne Nachweis dürfen Sie verwenden, dass gilt: $f^{\prime}(x)=-\frac{1}{160} x^{3}+\frac{3}{40} x^{2}-\frac{9}{40} x+\frac{1}{5}$

Zeigen Sie, dass der Graph von $f$ an der Stelle $x=12$ eine Nullstelle hat und $t(x)=-\frac{5}{2} x+30$ die Gleichung der Tangente an den Graphen von $f$ an dieser Stelle angibt. (5BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Nachweis der Tangente
Berechne $f'(12)$ :
$f^{\prime}(12)=-\frac{1}{160} \cdot 12^{3}+\frac{3}{40} \cdot12^{2}-\frac{9}{40}\cdot 12+\frac{1}{5}=-\dfrac{5}{2}$
Das ist ebenfalls die Steigung der Geraden $t$ , was für eine Tangente gelten muss.
Weiterhin ist $t(12)=-\frac{5}{2}\cdot 12+30= 0$ und $f(12) = 0$ .
Damit sind die Vorgaben gezeigt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeige:
$f'(12)=-\dfrac{5}{2}$
$t(12) = f(12) = 0$
Untersuchen Sie für jede der drei folgenden Aussagen die Gültigkeit mithilfe des Graphen von $f^{\prime}$ :
I. Die Funktion $f$ ist überall monoton steigend.
II. An der Stelle $x=6$ hat die Funktion $f$ kein lokales Maximum.
III. Die Tangente an den Graphen von $f$ im Punkt $(0{,}5 \mid f(0{,}5))$ ist parallel zu zwei weiteren Tangenten an den Graphen von $f$ .
(7BE)

Veranschaulichung der Graphen
Darstellung der Graphen
Der grüne Graph gehört zur Funktion $f$ und der orangefarbige Graph gehört zu $f'.$
I. Die Funktion $f$ ist überall monoton steigend.
Die Aussage I ist falsch, da der Graph von $f'$ Punkte unterhalb der x-Achse hat.
II. An der Stelle $x=6$ hat die Funktion $f$ kein lokales Maximum.
Die Aussage II ist richtig, da die Funktion $f'$ an der Stelle $x=6$ keine Nullstelle
besitzt.
III. Die Tangente an den Graphen von $f$ im Punkt $(0{,}5 \mid f(0{,}5))$ ist parallel zu zwei weiteren Tangenten an den Graphen von $f$
Tangenten der Graphen
Eingezeichnet in die Abbildung ist der Graph der Tangente im Punkt $(0{,}5|f(0{,}5))$ .
Es ist $f'(0{,}5)=\dfrac{27}{256}$ .
Weiterhin ist die Gerade $y=\dfrac{27}{256}$ in der Abbildung eingezeichnet.
Die Gerade schneidet $f'$ in drei Punkten, d.h. es gibt insgesamt drei Punkte am Graphen von $f$ mit gleicher Steigung und demnach drei parallele Tangenten.
Demnach ist die Aussage III richtig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Graph der in $\mathbb{R}$ definierten Funktion $h$ mit $h(x)=f^{\prime}(x+4)-\frac{1}{10}$ ist symmetrisch bezüglich des Koordinatenursprungs.
Geben Sie die Symmetrie des Graphen von $f^{\prime}$ an und begründen Sie Ihre Angabe ausgehend vom Graphen von $h$ . (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Die Symmetrie des Graphen von $f^{\prime}$
Der Graph von $h$ kann aus dem Graphen von $f'$ erzeugt werden durch eine
Verschiebung um $4$ in negative x-Richtung und um $\dfrac{1}{10}$ in negative
y-Richtung.
Begründung ausgehend vom Graphen von $h$
Die Funktion $h$ ist punktsymmetrisch zum Koordinatenursprung.
Damit ist auch der Graph von $f'$ punktsymmetrisch, und zwar bezüglich des
Punktes $\left(4\Big\vert\dfrac{1}{10}\right)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Ermittle die Verschiebung des Graphens in x- und y-Richtung.
Teil 2
Die Funktion $h$ ist punktsymmetrisch zum Koordinatenursprung.
Durch die Verschiebung bleibt die Punktsymmetrie erhalten, nur zu einem anderen Punkt.
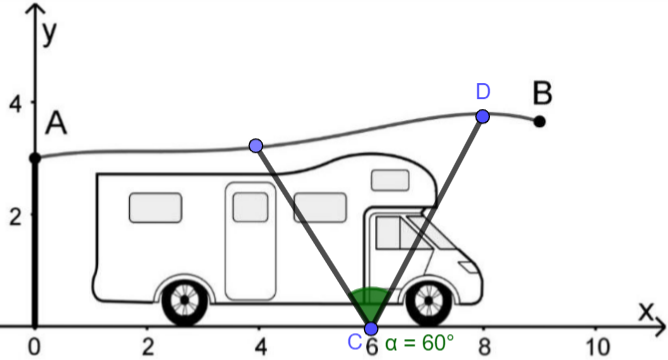
Die Abbildung zeigt einen Längsschnitt eines Carports für ein Wohnmobil. Das Dach des Carports ist in Querrichtung nicht geneigt. Im Folgenden sollen die Materialstärken der Bauteile des Carports vernachlässigt werden.
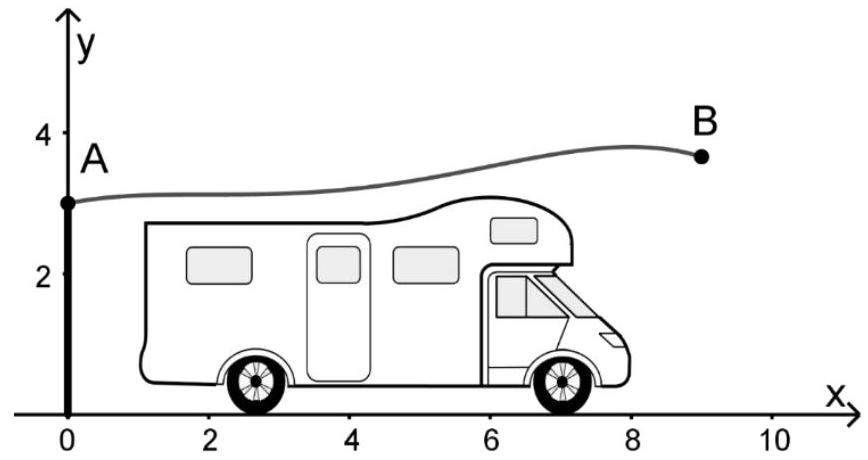
Die Profillinie des Längsschnitts des Dachs wird zwischen den Punkten $A(0 \mid 3)$ und $B(9 \mid f(9))$ modellhaft mithilfe der Funktion $f$ beschrieben.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. Die $x$ -Achse stellt den horizontalen Untergrund dar.
Untersuchen Sie, ob ein Wohnmobil mit einer Länge von $7{,}05$ m und einer Höhe von $3{,}10 \mathrm{~m}$ vollständig im Carport untergestellt werden kann. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Kann ein Wohnmobil mit einer Länge von $7{,}05$ m und einer Höhe von $3{,}10 \mathrm{~m}$ vollständig im Carport untergestellt werden?
Untersuche, ob im Bereich $0\leq x\leq 9$ die Funktionswerte der Funktion $f$ mindestens den Wert $3{,}1$ haben.
Löse die Gleichung $f(𝑥) = 3{,}10$ :
Für $0 ≤ x ≤ 9$ liefert der GTR die Lösung $x\approx0{,}797536...$ $\;\Rightarrow\;x\approx 0{,}8$ .
Die Abbildung zeigt dann, dass der Carport auf einer Länge von etwa $8{,}20 \;\text{m}$ ausreichend hoch ist ( $9\;\text{m} -0{,}80\;\text{m} =8{,}20\;\text{m}$ ).
Das Wohnmobil kann also theoretisch vollständig untergestellt werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Löse die Gleichung $f(x)=3{,}1$ und vergleiche mit der Abbildung.
Die maximale Neigung von Carportdächern sollte bei $25\;\%$ liegen. Untersuchen Sie, ob das betrachtete Carportdach diese Eigenschaft erfüllt. (4BE)
Untersuche, ob die maximale Neigung des Carportdachs höchstens $25\;\%$ beträgt
Die maximale Neigung existiert dort, wo $f'$ ein Maximum oder ein Minimum
besitzt.
Im Bereich $0\leq x\leq 9$ nimmt $f'(x)$ den kleinsten Wert an der Intervallgrenze $x=9$ an. (Siehe auch die Abbildung bei Aufgabe b).)
Es ist $f'(9)\approx-0{,}30625\;\Rightarrow\;f'(9)\approx-0{,}31$ .
Der Carport hat eine Neigung von etwa $31\;\%$ und erfüllt die Vorgabe nicht.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die maximale Neigung existiert dort, wo $f'$ ein Maximum oder ein Minimum besitzt.
Betrachte den Graphen von $f'(x)$ und suche im Bereich $0\leq x\leq 9$ den kleinsten Wert. $\;\Rightarrow\;x_1$
Berechne $f'(x_1)$ , gib die Neigung in Prozent an und vergleiche mit der vorgegebenen Neigung.
Abgesehen von einem $20 \mathrm{~cm}$ hohen Streifen unmittelbar über dem Untergrund ist der Carport auf einer Seite über seine gesamte Länge vollständig verkleidet. Die Verkleidung ist eben und vertikal angebracht.
Berechnen Sie den Inhalt der verkleideten Fläche. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Der Inhalt der verkleideten Fläche
Berechne das Integral über $f(x)$ im Bereich $\leq x\leq 9$ und ziehe den $20 \mathrm{~cm}$ hohen und $9 \mathrm{~m}$ breiten Streifen ab.
Berechne $\displaystyle\int_0^9f(x)\;dx-9\cdot0{,}2\approx28{,}5159375$ .
Der Flächeninhalt der verkleideten Fläche beträgt etwa $29 \mathrm{~m}^2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $A=\displaystyle\int_0^9f(x)\;dx-9\cdot 0{,}2$ .
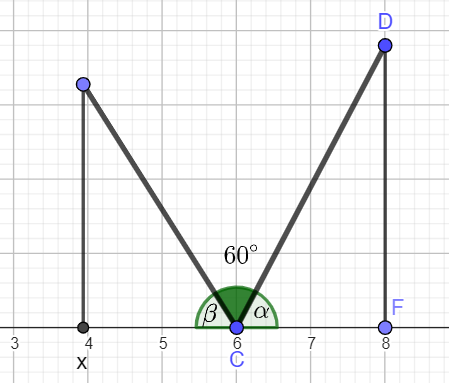
Ausgehend vom selben Punkt des Untergrunds verlaufen entlang der seitlichen Verkleidung des Carports zwei geradlinige Stützen jeweils bis zum Dach. Die Stützen schließen einen Winkel mit einer Größe von $60°$ ein. Die Endpunkte der ersten Stütze werden im Modell durch $C(6|0)$ und $D(8|f(8))$ dargestellt.
Zeichnen Sie die beiden Stützen in die Abbildung ein.
Berechnen Sie die $x$ -Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt. (7BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel konstruieren
Die $x$ -Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt
Es ist $\tan \alpha=\dfrac{f(8)}{8-6}=\dfrac{3{,}8}{2}=1{,}9\;\Rightarrow\;\alpha=\tan^{-1}(1{,}9)\approx 62{,}2^\circ$
Dann ist der Winkel $\beta=180^\circ-62{,}2^\circ-60^\circ\approx 57{,}8^\circ$
Dann gilt: $\tan 57{,}8^\circ=\dfrac{f(x)}{6-x}$
Für die Lösung der Gleichung muss das Gradmaß in das Bogenmaß umgewandelt werden: $57{,}8^\circ\cdot \dfrac{\pi}{180^\circ}\approx1{,}0088\; \text{rad}$
Löse nun die Gleichung $\tan(1{,}0088)=\dfrac{f(x)}{6-x}$
Im Bereich $0\leq x\leq 9$ liefert der GTR die Lösung $x\approx 3{,}985744026\;\Rightarrow\;$ $x\approx 4$ .
Die $x$ -Koordinate des Punktes, der den Endpunkt der zweiten Stütze am Dach darstellt, beträgt etwa $4$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Markiere in der Skizze die Punkte $C$ und $D$ . Zeichne die Strecke $\overline{CD}$ ein.
Trage dann im Punkt $C$ den Winkel $60^\circ$ an. Verlängere den Schenkel bis zum Carport.
Teil 2
Berechne den Neigungswinkel der ersten Stütze $\;\Rightarrow\;\alpha$
Der Neigungswinkel der zweiten Stütze ist dann $\beta=180^\circ-\alpha-60^\circ$
Löse dann die Gleichung $\tan \beta=\dfrac{f(x)}{6-x}$ nach $x$ auf.

4

Aufgabe 2A

In einem Paketzentrum werden pro Jahr viele Millionen Pakete angeliefert. Die Pakete werden automatisch nach ihrem Bestimmungsort sortiert. $10 \%$ der Pakete haben das Ziel A, $7 \%$ das Ziel B. Die übrigen Pakete haben andere Ziele.

Bestimmen Sie die Wahrscheinlichkeit dafür, dass von $100$ zufällig ausgewählten Paketen
- genau neun das Ziel B haben.
- weniger als neun das Ziel B haben.
(4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Genau neun Pakete haben das Ziel B
$X$ : Ist die Anzahl der Pakete, die das Ziel B haben
$X$ ist binomialverteilt mit $p = 0{,}07$ und $n= 100.$
Gesucht ist:
$P(X=9)=\text{binompdf}(100, 0.07{,}9)\approx 0{,}104$
Die Wahrscheinlichkeit, dass von $100$ zufällig ausgewählten Paketen genau neun das Ziel $B$ haben, beträgt rund $10\;\%$ .
Weniger als neun Pakete haben das Ziel B
Gesucht ist:
$P(X<9)=P(X\leq 8)=\text{binomcdf}(100, 0.07{,}8)\approx 0{,}734$
Die Wahrscheinlichkeit dafür, dass von $100$ zufällig ausgewählten Paketen weniger als neun das Ziel B haben, beträgt rund $73\;\%.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$X$ : Ist die Anzahl der Pakete, die das Ziel B haben.
$X$ ist binomialverteilt mit $p = 0{,}07$ und $n= 100.$
Teil 1
Gesucht ist: $P(X=9)$
Teil 2
Gesucht ist: $P(X< 9)$
Unter $100$ zufällig ausgewählten Paketen haben genau neun das Ziel B.
Berechnen Sie die prozentuale Abweichung dieser Anzahl vom Erwartungswert für die
Anzahl von Paketen mit dem Ziel B unter 100 zufällig ausgewählten Paketen. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Prozentuale Abweichung der Anzahl vom Erwartungswert
Die Anzahl ist $9$ und es ist $\mu=n\cdot p= 100\cdot 0{,}07=7$ .
Dann gilt für die prozentuale Abweichung: $\dfrac{9-7}{7}=\dfrac{2}{7}\approx0{,}286$
Die prozentuale Abweichung der Anzahl neun vom Erwartungswert für die Anzahl von Paketen mit dem Ziel $B$ unter $100$ zufällig ausgewählten Paketen, beträgt rund $29\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Anzahl ist $9$ und es ist $\mu=n\cdot p$ .
Berechne $\mu$ und die prozentuale Abweichung von $9$ und $\mu$ .
Im Paketzentrum werden $20$ Pakete zufällig ausgewählt.
Eines der anderen Ziele ist Ziel C. Die Wahrscheinlichkeit dafür, dass von den $20$ ausgewählten Paketen keines das Ziel C hat, beträgt etwa $54 \%$ .
Ermitteln Sie den Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden
Es ist $Y$ die Anzahl der Pakete, die das Ziel $C$ haben.
$Y$ ist binomialverteilt mit $n = 20$ und $p$ .
Dabei ist $p$ der Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden.
Gegeben ist:
Die Wahrscheinlichkeit dafür, dass von den $20$ ausgewählten Paketen keines das Ziel $C$ hat, beträgt etwa $54 \;\%$ .
Gesucht ist:
$P(Y=0)= 0{,}54 \;\Rightarrow\;P(Y=0)=\text{binompdf}(20, p,0)=0{,}54$
$\Rightarrow\;\begin{pmatrix}20\\0\end{pmatrix}\cdot p^0\cdot (1-p)^{20-0}=0{,}54$
Daraus folgt die Gleichung $(1 − p)^{20} = 0{,}54$ .
Der GTR liefert als Lösung dieser Gleichung $p\approx 0{,}0303395...$ .
Der Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden, beträgt rund $3\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es ist $Y$ die Anzahl der Pakete, die das Ziel $C$ haben.
$Y$ ist binomialverteilt mit $n = 20$ und $p$ .
Gesucht ist: $P(Y=0)= 0{,}54$
Die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang kann mit dem Term
berechnet werden.

Geben Sie ein passendes Ereignis an. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Geben Sie ein passendes Ereignis an
Es ist $P(A)=0{,}1$ und $P(\overline{A})=1-0{,}1=0{,}9$ .
Dann ist der Term $0{,}9^{14}$ die Wahrscheinlichkeit dafür, dass von den $20$ ausgewählten Paketen die ersten $14$ nicht das Ziel $A$ haben.
In der eckigen Klammer steht der Term für $n=6$ und $p=0{,}1$ :
$P(X\leq 3)=\underbrace{\begin{pmatrix}6\\0\end{pmatrix}\cdot 0{,}1^0 \cdot 0{,}9^6}_{P(X=0)}+\underbrace{\begin{pmatrix}6\\1\end{pmatrix}\cdot 0{,}1^1 \cdot 0{,}9^5}_{P(X=1)}+\underbrace{\begin{pmatrix}6\\2\end{pmatrix}\cdot 0{,}1^2 \cdot 0{,}9^4}_{P(X=2)}\\\qquad\qquad~~+\underbrace{\begin{pmatrix}6\\3\end{pmatrix}\cdot 0{,}1^3 \cdot 0{,}9^3}_{P(X=3)}$
Dieser Term bedeutet, "von $6$ Paketen haben höchstens $3$ Pakete das Ziel $A$ ".
Insgesamt ergibt sich dann folgendes Ereignis:
Von den $20$ ausgewählten Paketen haben die ersten $14$ nicht das Ziel $A$ und von
den weiteren $6$ Paketen haben höchstens $3$ das Ziel $A$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte den Term vor der Klammer $0{,}9^{14}$ . Was besagt er?
Betrachte dann den Term in der eckigen Klammer. Was besagt er?
Alle im Paketzentrum angelieferten Pakete werden im Rahmen der Sortierung gewogen.
$5 \%$ der Pakete haben ein Gewicht von mehr als $10 \mathrm{~kg}$ und gelten damit als schwer. Von den Paketen mit dem Ziel A sind $8 \%$ schwer.
Ein Paket wird zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:
$S$ : „Das ausgewählte Paket ist schwer.“
A: „Das ausgewählte Paket hat das Ziel A.“
Der Sachzusammenhang ist in der Vierfeldertafel dargestellt.
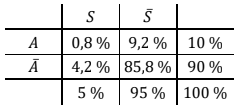
Untersuchen Sie, ob der Anteil der Pakete mit Ziel A unter den schweren Paketen ebenso groß ist wie unter den nicht-schweren Paketen. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Ist der Anteil der Pakete mit Ziel $A$ unter den schweren Paketen ebenso groß ist wie unter den nicht-schweren Paketen?
Der Anteil mit Ziel $A$ unter den schweren Paketen ist:
$\dfrac{P(A \cap S)}{P(S)}=\dfrac{0{,}8 \;\%}{5 \;\%}=16 \;\%$ .
Der Anteil mit Ziel $A$ unter den nicht-schweren Pakten ist:
$\dfrac{P(A \cap \overline{S})}{P(\overline{S})}=\dfrac{9{,}2 \;\%}{95 \;\%}\approx9{,}7 \;\%$
Wie man sieht, sind die Anteile unterschiedlich.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $\dfrac{P(A \cap S)}{P(S)}$ und $\dfrac{P(A \cap \overline{S})}{P(\overline{S})}$ und vergleiche.
Von den Paketen, die das Ziel B haben, sind $2 \;\%$ schwer.
Berechnen Sie den Anteil der schweren Pakete unter denen, die weder Ziel A noch Ziel B haben. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Anteil der schweren Pakete unter denen, die weder Ziel A noch Ziel B haben
Der Anteil der schweren Pakete unter denen, die weder Ziel A noch Ziel B haben, ist $x.$
Weiterhin ist bekannt:
$10 \;\%$ der Pakete haben das Ziel $A$ , $7\; \%$ das Ziel $B$ . Die übrigen Pakete haben andere Ziele.
Von den Paketen mit dem Ziel $A$ sind $8 \;\%$ schwer.
Von den Paketen, die das Ziel $B$ haben, sind $2 \;\%$ schwer.
Wenn $10 \;\%$ der Pakete das Ziel $A$ haben, und $7\; \%$ das Ziel $B$ haben, dann haben $100\;\%-(10\;\%+7\;\%)$ andere Ziele, hier $C$ genannt.
Es ist $P(S)=P(A \cap S)+P(B \cap S)+P(C \cap S)$
Setzt man die bekannten Werte ein, so ergibt sich die folgende Gleichung:
$0{,}05=0{,}1\cdot 0{,}08+0{,}07\cdot 0{,}02+(1-(0{,}1+0{,}07))\cdot x$
Der GTR liefert als Lösung dieser Gleichung $x\approx0{,}04891566...$ .
Der Anteil der schweren Pakete unter denen, die weder Ziel $A$ noch Ziel $B$ haben, beträgt rund $4{,}9\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle eventuell ein Baumdiagramm mit den Zielen $A$ , $B$ und $C$ (andere Ziele) und den Anteilen der schweren Pakete zu den jeweiligen Zielen.
Erstelle eine Gleichung für $P(S)$ . Bekannt ist $P(S)=0{,}05.$

5

Aufgabe 2B

Ein Unternehmen stellt Tischtennisbälle her. $98 \%$ der hergestellten Bälle weichen nur unwesentlich von der Kugelform ab; diese werden im Weiteren als „rund“ bezeichnet, die übrigen als „unrund“. Aus der großen Menge der hergestellten Bälle werden regelmäßig Stichproben entnommen, wobei die Auswahl der Bälle für jede Stichprobe als zufällig angenommen werden kann. Die Zufallsgröße $X$ gibt die Anzahl der runden Bälle in diesen Stichproben an. $X$ ist binomialverteilt.

Es wird eine Stichprobe von $200$ Bällen untersucht.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Stichprobe
- nur runde Bälle enthält,
- mindestens $190$ runde Bälle enthält,
- genau einen oder genau zwei unrunde Bälle enthält.
(4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Gegeben sind $n=200$ und $p=0{,}98$ .
Nur runde Bälle sind in der Stichprobe enthalten
Gesucht ist $P(X=200)=\text{binompdf}(200;0{,}98;200)\approx0{,}01758$
Die Wahrscheinlichkeit dafür, dass die Stichprobe nur runde Bälle enthält, beträgt rund $1{,}8\;\%$ .
Die Stichprobe mindestens $190$ runde Bälle enthält
Gesucht $P(X\geq 190)=\text{binomcdf}(200{,}0.98{,}190{,}200)\approx0{,}997$ 5
Die Wahrscheinlichkeit dafür, dass die Stichprobe mindestens $190$ runde Bälle enthält, beträgt rund $99{,}8\;\%$ .
Die Stichprobe genau einen oder genau zwei unrunde Bälle enthält
Ist genau $1$ Ball nicht rund, dann sind $199$ Bälle rund.
Sind genau $2$ Bälle nicht rund, dann sind $198$ Bälle rund.
Gesucht ist also $P(198\leq X\leq 199)=\text{binomcdf}(200{,}0.98{,}198{,}199)\approx0{,}2176$
Die Wahrscheinlichkeit dafür, dass die Stichprobe genau einen oder genau zwei unrunde Bälle enthält, beträgt rund $21{,}8 \;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für alle Teilaufgaben gilt: $n=200$ und $p=0{,}98$
Teil 1
Berechne $P(X=200)$ .
Teil 2
Berechne $P(X\geq 190)$ .
Teil 3
Berechne $P(198\leq X\leq 199)$ .
Nach der Herstellung durchlaufen die Bälle eine Sortieranlage. Dabei wird ein unrunder Ball mit einer Wahrscheinlichkeit von $90 \%$ aussortiert. Allerdings werden auch $5 \%$ der runden Bälle aussortiert.
Stellen Sie den Prozess der Herstellung und Sortierung der Bälle in einem beschrifteten Baumdiagramm dar. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Baumdiagramm anlegen
Es werden die Ereignisse festgelegt:
$R$ : der Ball ist rund
$A$ : der Ball wird aussortiert
Nach Aufgabe a) gilt:
$98\;\%$ der hergestellten Bälle sind rund.
$100\;\%-98\;\%=2\;\%$ der hergestellten Bälle sind dann nicht rund.
Aus dem Aufgabentext b) folgt:
Ein unrunder Ball wird mit einer Wahrscheinlichkeit von $90 \%$ aussortiert.
Allerdings werden auch $5 \%$ der runden Bälle aussortiert.
Übertrage die Werte in ein Baumdiagramm:
Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Übertrage die gegebenen Werte aus Aufgabe a) und aus Aufgabe b) in ein Baumdiagramm.
Beschreiben Sie die Bedeutung des Terms $0{,}98 \cdot 0{,}05 \cdot 2000$ im Sachzusammenhang. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Bedeutung des Terms $0{,}98 \cdot 0{,}05 \cdot 2000$ im Sachzusammenhang
Es ist $n=2000$ und $0{,}98\cdot 0{,}05=P(R\cap A)$ (siehe Baumdiagramm).
Dann ist $\mu=n\cdot p=2000\cdot 0{,}98\cdot 0{,}05=98$ der Erwartungswert, dass von $2000$ hergestellten Bällen diese Anzahl ( $98$ ) von runden Bällen aussortiert werden.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Es wird ein Erwartungswert berechnet. Welcher?
Angenommen, die nicht aussortierten Bälle würden die gleiche Sortieranlage ein zweites Mal durchlaufen.
Begründen Sie, dass die Wahrscheinlichkeit dafür, dass ein nach zweimaligem Durchlaufen der Anlage zufällig ausgewählter Ball unrund ist und nicht aussortiert wird, $0{,}02 \cdot 0{,}1^{2}$ ist.

Berechnen Sie den Anteil der unrunden Bälle unter denjenigen, die dann nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pfadregeln
Nachweis der Wahrscheinlichkeit: $0{,}02 \cdot 0{,}1^{2}$
Ein Ball ist mit einer Wahrscheinlichkeit von $0{,}02$ unrund und wird beim
zweimaligen Durchlaufen der Anlage mit einer Wahrscheinlichkeit von $0{,}1\cdot 0{,}1=0{,}1^2$ nicht aussortiert. Mit den Pfadregeln ergibt sich für die Wahrscheinlichkeit $0{,}02 \cdot 0{,}1^2$ .
Anteil der unrunden Bälle unter denjenigen, die dann nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden
Ein Ball ist mit einer Wahrscheinlichkeit von $0{,}98$ rund und wird beim
zweimaligen Durchlaufen der Anlage mit einer Wahrscheinlichkeit von $0{,}95\cdot 0{,}95=0{,}95^2$ nicht aussortiert. Mit den Pfadregeln ergibt sich für die Wahrscheinlichkeit $0{,}98 \cdot 0{,}95^2$ .
Insgesamt gilt $P(\overline{A})=0{,}98 \cdot 0{,}95^2+0{,}02 \cdot 0{,}1^2$ .
Dann ergibt sich der gesuchte Anteil zu:
Der Anteil der unrunden Bälle unter denjenigen, die nach zweimaligem Durchlaufen der Anlage nicht aussortiert würden, beträgt rund $0{,}023\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Berechne mit den Pfadregeln, dass ein unrunder Ball beim zweimaligen Durchlaufen der Anlage nicht aussortiert wird $\;\Rightarrow\;0{,}02 \cdot 0{,}1^2$
Teil 2
Berechne $P(\overline{A})$ . Dann gilt für das gesuchte Verhältnis $\dfrac{0{,}02 \cdot 0{,}1^2}{P(\overline{A})}$ .
Das Gewicht eines Tischtennisballs soll $2{,}70$ Gramm (g) betragen. Bei einer Kontrolle einer sehr großen Anzahl von Bällen der Produktion wurden die in der Tabelle aufgeführten relativen Häufigkeiten für die Gewichte der Bälle festgestellt.
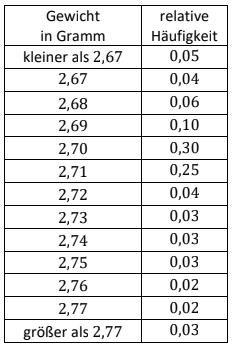
Begründen Sie, warum es nicht möglich ist, zu den in der Tabelle vorliegenden Daten das arithmetische Mittel der Gewichte zu berechnen. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufgaben zum arithmetischen Mittel
Warum ist es nicht möglich, das arithmetische Mittel der Gewichte zu berechnen
In der ersten und letzten Zeile der Tabelle sind Messdaten zusammengefasst. Für das arithmetische Mittel aller Gewichte muss jedes einzelne Gewicht bekannt sein und wie oft es vorkommt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die erste und letzte Zeile der Tabelle.
Die relativen Häufigkeiten aus der Tabelle werden im Folgenden als Wahrscheinlichkeiten verwendet.
Geben Sie das größte Gewicht an, das ein zufällig ausgewählter Ball mit einer Wahrscheinlichkeit von höchstens $20 \%$ unterschreitet. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relative Häufigkeit
Das größte Gewicht an, das ein zufällig ausgewählter Ball mit einer Wahrscheinlichkeit von höchstens $20\;\%$ unterschreitet
Die relativen Häufigkeiten aus der Tabelle werden im Folgenden als Wahrscheinlichkeiten verwendet.
In der Tabelle gibt es zwei Wahrscheinlichkeiten, die über $20\;\%$ liegen. Die nächste unter $20\;\%$ liegende Wahrscheinlichkeit ist $10\;\%$ .
Dazu gehört das Gewicht $2{,}69\;\text{g}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Suche in der Tabelle die größte unter $20\;\%$ liegende Wahrscheinlichkeit aus.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass in einer Stichprobe von $24$ zufällig ausgewählten Bällen höchstens einer ein Gewicht aufweist, das kleiner als $2{,}67$ g oder größer als $2{,}77$ g ist. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit, dass in einer Stichprobe von $24$ zufällig ausgewählten Bällen höchstens einer ein Gewicht aufweist, das kleiner als $2{,}67$ g oder größer als $2{,}77$ g ist
Die Variable $Y$ ist die Zahl der Bälle, die ein Gewicht aufweisen, das kleiner als $2{,}67\;\text{g}$ oder größer als $2{,}77\;\text{g}$ ist.
$Y$ ist binomialverteilt mit $n=24$ und $p=0{,}05+0{,}03=0{,}08$ .
Gesucht ist $P(Y\leq 1)$ :
$P(Y\leq 1)=\text{binomcdf}(24{,}0.08{,}0,1)\approx0{,}4173$
Die Wahrscheinlichkeit, dass in einer Stichprobe von $24$ zufällig ausgewählten Bällen höchstens einer ein Gewicht aufweist, das kleiner als $2{,}67$ g oder größer als $2{,}77$ g ist, beträgt rund $41{,}7\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$Y$ ist die Zahl der Bälle, die ein Gewicht aufweisen, das kleiner als $2{,}67\;\text{g}$ oder größer als $2{,}77\;\text{g}$ ist.
$Y$ ist binomialverteilt mit $n=24$ und $p=p_1+p_2$ (entnimm diese Werte der Tabelle).
Gesucht ist $P(Y\leq 1)$ .

6

Aufgabe 2C

Betrachtet wird die Gruppe der in Deutschland lebenden Personen, die eine Pkw-Fahrerlaubnis haben. $47{,}5 \%$ dieser Personen interessieren sich für den Kauf eines Elektroautos, $43{,}4 \%$ kaufen in Bioläden ein, $34{,}7 \%$ interessieren sich nicht für den Kauf eines Elektroautos und kaufen nicht in Bioläden ein.

Der beschriebene Sachverhalt wird in einer Vierfeldertafel dargestellt. Dazu werden die folgenden Ereignisse betrachtet:
$B$ : Eine Person mit Pkw-Fahrerlaubnis kauft in Bioläden ein.
$E$ : Eine Person mit Pkw-Fahrerlaubnis interessiert sich für den Kauf eines Elektroautos.
Füllen Sie die Vierfeldertafel vollständig aus. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Die Vierfeldertafel vollständig ausgefüllt
Aus der Aufgabenstellung
Aus dem Aufgabentext entnimmt man $P(E)=47{,}5\;\%$ .
Dann ist $P(\overline{E})=1-P(E)=52{,}5\;\%$ .
Weiterhin ist $P(B)=43{,}4\;\%$ und
$P(\overline{B})=1-P(B)=56{,}6\;\%$ .
$34{,}7\; \%$ interessieren sich nicht für den Kauf eines Elektroautos und kaufen nicht in Bioläden ein $\;\Rightarrow\;P(\overline{E}\cap \overline{B})=34{,}7\;\%$
Berechnen in der Vierfeldertafel
Dann ergibt sich $P(\overline{E}\cap {B})=P(E)-P(\overline{E}\cap \overline{B})=52{,}5\;\%-34{,}7\;\%=17{,}8\;\%$
Es folgt dann $P({E}\cap \overline{B})=P(\overline{B})-P(\overline{E}\cap \overline{B})=56{,}6\;\%-34{,}7\;\%=21{,}9\;\%$ .
Der letzte Wert ist dann: $P({E}\cap {B})=P(E)-P({E}\cap \overline{B})=47{,}5\;\%-21{,}9\;\%=25{,}6\;\%$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Fülle mit den gegebenen Werten die Vierfeldertafel aus.
Verwende die Summen der Werte in den Zeilen und Spalten, um den Rest der Tafel auszufüllen.
Beurteilen Sie die Gültigkeit der folgenden Aussage: (2BE)
In der betrachteten Gruppe interessieren sich unter denjenigen, die in Bioläden einkaufen, mehr als die Hälfte für den Kauf eines Elektroautos.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel
Aussage bewerten
In der betrachteten Gruppe interessieren sich unter denjenigen, die in Bioläden einkaufen, mehr als die Hälfte für den Kauf eines Elektroautos
Die Aussage ist richtig, da $P({E}\cap {B})=25{,}6\;\%>P(\overline{E}\cap {B})=17{,}8\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Vergleiche $P({E}\cap {B})$ mit $P(\overline{E}\cap {B})$ .
Aus der betrachteten Gruppe werden 30 Personen zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass mindestens zwei Drittel der ausgewählten Personen am Kauf eines Elektroautos nicht interessiert sind. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Wahrscheinlichkeit berechnen
Es ist $X$ die Anzahl von Personen mit Pkw-Fahrerlaubnis, die nicht am Kauf eines Elektroautos interessiert sind. $X$ ist binomialverteilt mit $n=30$ und $p=0{,}525$ .
Zwei Drittel der ausgewählten Personen sind $\;\dfrac{2}{3}\cdot30=20$ .
Gesucht ist also: $P(X\geq 20)=1-P(X\leq 19)=1-\text{binomCdf}(30{,}0.525{,}0,19)\approx0{,}0842$
Die Wahrscheinlichkeit dafür, dass mindestens zwei Drittel der ausgewählten Personen am Kauf eines Elektroautos nicht interessiert sind, beträgt rund $8{,}4\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne $\dfrac{2}{3}$ der ausgewählten Personen. $\;\Rightarrow\;x_1$
Berechne $P(X\geq x_1)$ , wobei $X$ binomialverteilt ist mit $n=30$ und $p=0{,}525$ .
Unter den Elektroautos eines Herstellers weisen $30 \%$ mindestens eines der beiden Ausstattungsmerkmale A bzw. B auf; $10 \%$ der Elektroautos dieses Herstellers weisen das Merkmal A auf. Das abgebildete Baumdiagramm stellt den Sachverhalt dar. Die beiden Merkmale treten bei den Elektroautos des Herstellers unabhängig voneinander auf.
Geben Sie die Wahrscheinlichkeit dafür an, dass ein zufällig ausgewähltes Elektroauto des Herstellers keines der beiden Merkmale aufweist. (1BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Wahrscheinlichkeit, dass ein zufällig ausgewähltes Elektroauto des Herstellers keines der beiden Merkmale aufweist
Es ist $P({A}\cap {B})+P({A}\cap \overline{B})+ P(\overline{A}\cap {B})=0{,}3$ . (Auto weist eines der Merkmale auf)
$\Rightarrow\;P(\overline{A}\cap \overline{B})=1-\left(P({A}\cap {B})+P({A}\cap \overline{B})+ P(\overline{A}\cap {B})\right)=1-0{,}3=0{,}7$
Die Wahrscheinlichkeit, dass ein zufällig ausgewähltes Elektroauto des Herstellers keines der beiden Merkmale aufweist, beträgt $70\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Unter den Elektroautos eines Herstellers weisen $30 \%$ mindestens eines der beiden Ausstattungsmerkmale $A$ bzw. $B$ auf.
Berechne die Gegenwahrscheinlichkeit.

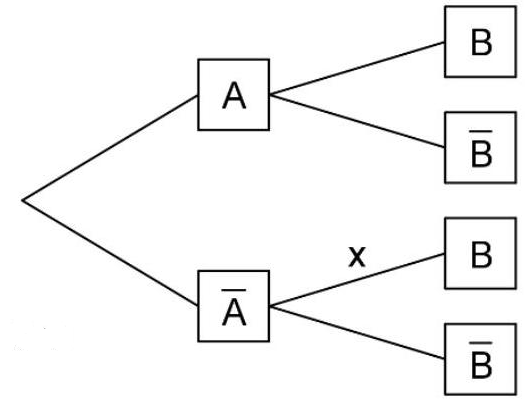
Ermitteln Sie den im Baumdiagramm genannten Anteil $x$ .

Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Elektroauto des Herstellers das Merkmal B aufweist. (4BE)

Beschreiben Sie im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term $1-10 \cdot 0{,}3 \cdot 0{,}7^{9}-0{,}7^{10}$ berechnet werden kann.
Geben Sie dieses Ereignis an. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm und Pfadregeln
Zufallsexperiment
Aus $10$ Elektroautos des Herstellers wird zufällig ausgewählt:
Ereignis
Es gilt: $P(X\geq 2)=1-P(X\leq 1)=1-\left(P(X=1)+P(X=0)\right)$
$P(X\geq 2)=1-\left(\begin{pmatrix}10\\1\end{pmatrix}\cdot0{,}3^1\cdot (1-0{,}3)^{10-1}+\begin{pmatrix}10\\0\end{pmatrix}\cdot0{,}3^0\cdot (1-0{,}3)^{n-0}\right)$
Mit $\begin{pmatrix}10\\1\end{pmatrix}=10$ , $\begin{pmatrix}10\\0\end{pmatrix}=1$ und $0{,}3^0=1$ folgt dann:
$P(X\geq 2)=1-10\cdot0{,}3^1\cdot 0{,}7^{9}-1\cdot 1\cdot 0{,}7^{10}$
Die rechte Seite entspricht dem gegebenen Term.
Ereignis: „Unter den zufällig ausgewählten Elektroautos weisen mindestens zwei
eines der beiden Merkmale $A$ und $B$ auf.“
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Betrachte einen Teil des gegebenen Terms: $10 \cdot 0{,}3 \cdot 0{,}7^{9}=\begin{pmatrix}10\\1\end{pmatrix}\cdot0{,}3^1\cdot (1-0{,}3)^{10-1}\;\Rightarrow\;n=10$
Teil 2
Wie berechnet man die folgende Wahrscheinlichkeit $P(X\geq 2)=1-P(X\leq 1)$ und welche Bedeutung hat sie?
Zehn Elektroautos des Herstellers werden nacheinander betrachtet.
Ermitteln Sie, wie viele Autos mit dem Merkmal A sich unter diesen zehn Autos mindestens befinden müssen, damit mit einer Wahrscheinlichkeit von mindestens $90 \%$ von den ersten drei betrachteten Autos mindestens eines das Merkmal A aufweist. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreimal-Mindestens-Aufgaben
Ermitteln Sie, wie viele Autos mit dem Merkmal $A$ sich unter diesen zehn Autos mindestens befinden müssen, damit mit einer Wahrscheinlichkeit von mindestens $90\; \%$ von den ersten drei betrachteten Autos mindestens eines das Merkmal $A$ aufweist
Gegeben sind $10$ Autos, davon haben $k$ Autos das Merkmal $A$ und $10-k$ Autos haben das Merkmal $A$ nicht. Betrachtet werden die ersten drei Autos.
Es ist also gesucht:
$P(\text{"mind. 1 Auto mit Merkmal A"})= 1- P(\text{"kein Auto mit Merkmal A"})\geq 0{,}9$
Für die ersten drei Autos gilt dann:
$P(\text{"kein Auto mit Merkmal A"})=\dfrac{10-k}{10}\cdot \dfrac{9-k}{9}\cdot \dfrac{8-k}{8}$
Dann muss folgende Ungleichung gelöst werden:
$P(\text{"mind. 1 Auto mit Merkmal A"})= 1- \left(\dfrac{10-k}{10}\cdot \dfrac{9-k}{9}\cdot \dfrac{8-k}{8}\right)\geq 0{,}9$
Der GTR liefert als Lösung der Gleichung $1- \left(\dfrac{10-k}{10}\cdot \dfrac{9-k}{9}\cdot \dfrac{8-k}{8}\right)= 0{,}9$ den Wert $k\approx4{,}759717094$ .
Bei $k$ handelt es sich um eine Anzahl, d.h. $k$ ist ganzzahlig. Also muss $k\geq 5$ sein
Es müssen sich mindestens $5$ Autos mit dem Merkmal $A$ unter diesen zehn Autos befinden, damit mit einer Wahrscheinlichkeit von mindestens $90\; \%$ von den ersten drei betrachteten Autos mindestens eines das Merkmal $A$ aufweist.
Anmerkung: Wenn $k$ die Werte $8, 9$ oder $10$ annimmt, dann ist das eine triviale Lösung, d.h. $p=100\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Gegeben sind $10$ Autos, davon haben $k$ Autos das Merkmal $A$ und $10-k$ Autos haben das Merkmal $A$ nicht. Betrachtet werden die ersten drei Autos.
Gesucht ist: $P(\text{"mind. 1 Auto mit Merkmal A"})= 1- P(\text{"kein Auto mit Merkmal A"})\geq 0{,}9$
Berechne für die ersten drei Autos $P(\text{"kein Auto mit Merkmal A"})$ und löse die Ungleichung.

7

Aufgabe 3A

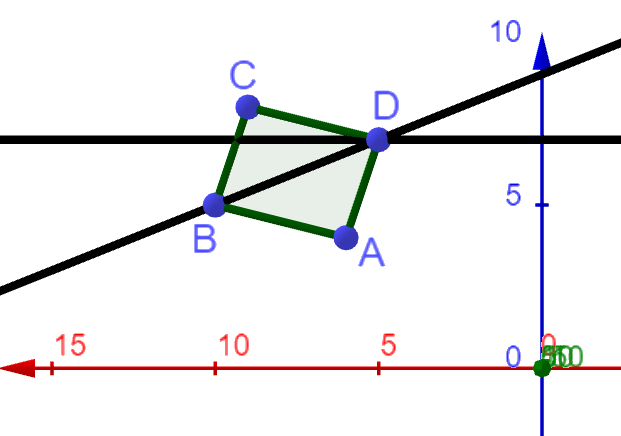
Ein Element eines Klettergartens ist eine ebene, viereckige Kletterwand. In einem Koordinatensystem können die Eckpunkte der Kletterwand durch die Punkte $A(6|7| 4), B(10|5| 5), C(9|5{,}5| 8)$ und $D(5|7{,}5| 7)$ beschrieben werden.

Die $x_{1} x_{2}$ -Ebene stellt den horizontalen Boden dar. Die Kletterwand liegt in einer Ebene, die senkrecht zur $x_{1} x_{2}$ -Ebene steht. Eine Längeneinheit im Koordinatensystem entspricht

$1$ Meter (m) in der Wirklichkeit.

Weisen Sie nach, dass die Kletterwand die Form eines Parallelogramms hat, aber nicht rechteckig ist. (4BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelogramm
Die Kletterwand hat die Form eines Parallelogramms, ist aber nicht rechteckig
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix}10\\5\\5\end{pmatrix}-\begin{pmatrix}6\\7\\4\end{pmatrix}=\begin{pmatrix}4\\-2\\1\end{pmatrix}$
$\overrightarrow{DC}=\overrightarrow{OC}-\overrightarrow{OD}=\begin{pmatrix}9\\5{,}5\\8\end{pmatrix}-\begin{pmatrix}5\\7{,}5\\7\end{pmatrix}=\begin{pmatrix}4\\-2\\1\end{pmatrix}$
Damit ist $\overrightarrow{AB}=\overrightarrow{DC}$ , d.h. diese gegenüberliegenden Seiten sind parallel und gleich lang. Die Länge muss gar nicht extra ausgerechnet werden, da die Vektoren identisch sind.
Weiterhin ist
$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}=\begin{pmatrix}5\\7{,}5\\7\end{pmatrix}-\begin{pmatrix}6\\7\\4\end{pmatrix}=\begin{pmatrix}-1\\0{,}5\\3\end{pmatrix}$ und
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=\begin{pmatrix}9\\5{,}5\\8 \end{pmatrix}-\begin{pmatrix}10\\5\\5 \end{pmatrix}=\begin{pmatrix}-1\\0{,}5\\3 \end{pmatrix}$
Also ist auch das zweite Paar gegenüberliegender Seiten parallel und gleich lang, es handelt sich also um ein Parallelogramm oder als Spezialfall um ein Rechteck.
Prüfe, ob es im Punkt $A$ einen rechten Winkel gibt.
Das Skalarprodukt zwischen $\overrightarrow{AB}$ und $\overrightarrow{AD}$ ist:
Es gibt keinen rechten Winkel im Punkt $A$ , d.h. die Kletterwand hat die Form eines Parallelogramms, ist aber nicht rechteckig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{DC}$ und vergleiche sie.
Prüfe, ob das Skalarprodukt zwischen $\overrightarrow{AB}$ und $\overrightarrow{AD}$ gleich null ist.
Auf der Kletterwand verläuft eine horizontale Linie, die den Punkt $D$ enthält. Diese Linie teilt die Wand in zwei Teile.
Begründen Sie, dass der Flächeninhalt des unteren Teils größer ist als der des oberen Teils. (4BE)
Der Flächeninhalt des unteren Teils ist größer als der des oberen Teils
Die folgende Abbildung ist nicht Teil der Aufgabenstellung. Sie dient nur zur Veranschaulichung.
In der Abbildung eingezeichnet ist die horizontale Linie, die den Punkt $D$ enthält.
Weiterhin ist eine Linie eingezeichnet, die durch die Punkte $B$ und $D$ verläuft und die Kletterwand in zwei gleich große Flächen einteilt. Da die $x_3$ -Koordinate von $D$ größer als die $x_3$ -Koordinate von $B$ ist, verläuft die horizontale Linie oberhalb der Linie, die durch die Punkte $B$ und $D$ verläuft.
Damit ist der Flächeninhalt des unteren Teils größer als der des oberen Teils.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Denke dir eine Linie durch die Punkte $B$ und $D$ , die die Fläche in zwei gleich große Teile teilt.
Vergleiche dann die $x_3$ -Koordinaten der Punkte $B$ und $D$ und vergleiche den Verlauf der horizontalen Linie im Vergleich zur gedachten Linie.
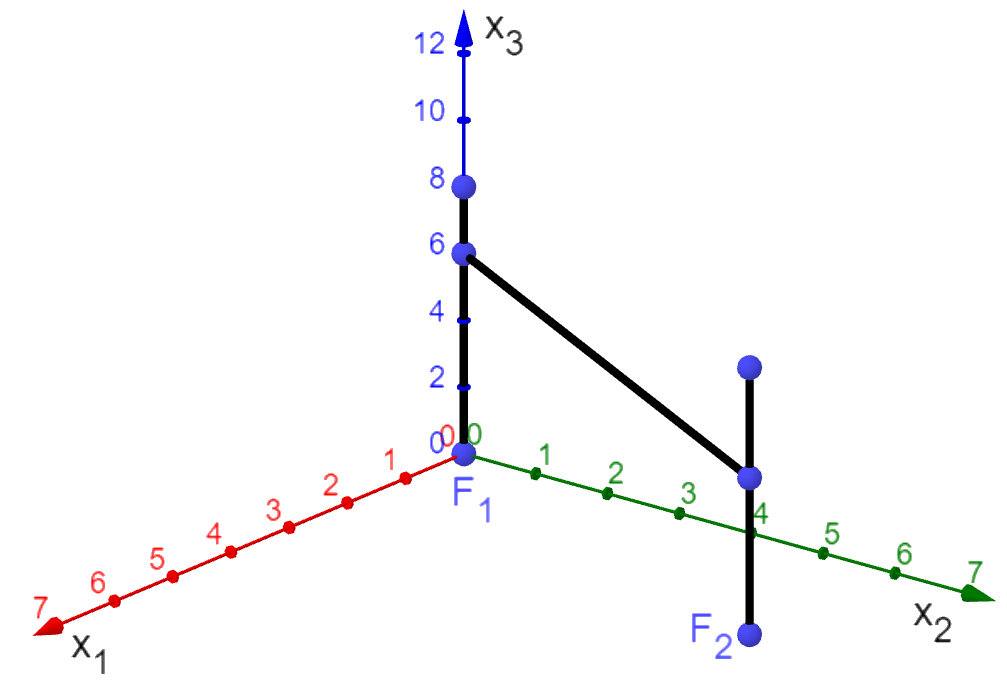
Ein anderes Element des Klettergartens ist ein Stahlseil, das zwischen zwei vertikal stehenden, $8 \mathrm{~m}$ hohen Masten gespannt ist. Der Fußpunkt des ersten Masts wird durch $F_{1}(0|0| 0)$ dargestellt, der Fußpunkt des zweiten Masts durch $F_{2}(2{,}5|6| 0)$ . Das Seil ist am ersten Mast in einer Höhe von $6 \mathrm{~m}$ befestigt, am zweiten Mast in einer Höhe von $4{,}7$ m. Es soll davon ausgegangen werden, dass das Seil geradlinig verläuft.
Stellen Sie die beiden Masten und das Seil in einem dreidimensionalen Koordinatensystem dar. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatengeometrie im Raum
Darstellung der beiden Masten und das Seil in einem dreidimensionalen Koordinatensystem
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichne $F_1$ und $F_2$ sowie die Endpunkte der Masten ein.
Verbinde die Punkte.
Zeichne einen Punkt in der Höhe $6$ auf dem 1. Masten und einen Punkt in der Höhe $4{,}7$ auf dem 2. Masten ein.
Verbinde die beiden Punkte.
Bestimmen Sie die Neigung des Seils zwischen den beiden Masten in Prozent. (4BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung und Steigungswinkel
Die Neigung des Seils zwischen den beiden Masten
Es ist der Vektor $\overrightarrow{F_1F_2}=\overrightarrow{OF_2}-\overrightarrow{OF_1}=\begin{pmatrix}2{,}5\\6\\0\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}=\begin{pmatrix}2{,}5\\6\\0\end{pmatrix}$ und sein Betrag ist $\left|\overrightarrow{F_1F_2}\right|=\sqrt{2{,}5^2+6^2+0^2}=\sqrt{42{,}25}=6{,}5$ .
Dann folgt für die Neigung des Seils:
$\text{Neigung}=\dfrac{\text{Höhendifferenz}}{\text{Länge der horizontalen Strecke}}=\dfrac{6-4{,}7}{6{,}5}=0{,}2$
Die Neigung des Seils zwischen den beiden Masten beträgt $20\;\%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Länge des Vektors $\overrightarrow{F_1F_2}$ .
Für die Neigung gilt: $\text{Neigung}=\dfrac{\text{Höhendifferenz}}{\text{Länge der horizontalen Strecke}}$
Über das bisher betrachtete Seil hinweg ist ein zweites Stahlseil gespannt. Dieses obere Seil verläuft entlang der Geraden $\def\arraystretch{1.25} h: \vec{x}=\left(\begin{array}{c}-1 \\ 3 \\ 8\end{array}\right)+t \cdot\left(\begin{array}{l}5 \\ 0 \\ 0\end{array}\right)$ mit $t \in \mathbb{R}$ .
Ein Punkt des oberen Seils liegt vertikal über einem Punkt des unteren Seils.
Ermitteln Sie den Abstand dieser beiden Punkte. (5BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zweier Geraden
Ermitteln Sie den Abstand der beiden Punkte
Das obere Seil verläuft entlang der Geraden $h:\;\vec x=\begin{pmatrix}-1\\3\\8\end{pmatrix}+t\cdot \begin{pmatrix}5\\0\\0\end{pmatrix}$ .
Die $x_2$ -Koordinate dieses Seils ist $x_2=3$ .
Das Stahlseil hat die Gleichung:
Die $x_2$ -Koordinate des Stahlseils ist $x_2=6\cdot r$ .
Beide $x_2$ -Koordinaten müssen für die beschriebenen Punkte gleich sein:
Die Höhe des Stahlseils ( $x_3$ -Koordinate von $g$ ) ist dann:
Die Höhe des oberen Seils ( $x_3$ -Koordinate von $h$ ) ist $x_3=8$ .
Die Differenz der beiden $x_3$ -Koordinaten ergibt den gesuchten Abstand der beiden Punkte.
Der Abstand der beiden Punkte beträgt $8-5{,}35=2{,}65\;\text{m}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Erstelle die Gleichung für das Stahlseil.
Die gesuchten Punkte haben die gleichen $x_2$ -Koordinaten

8

Aufgabe 3B

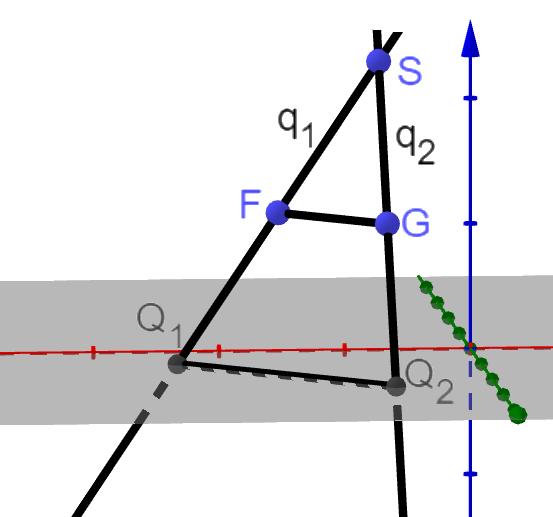
Betrachtet wird der Stumpf $A B C D E F G H$ der schiefen Pyramide $A B C D S$ . Die Grundfläche $A B C D$ mit $A(4|0| 0), B(4|4| 0), C(0|4| 0)$ und $D(0|0| 0)$ sowie die Deckfläche des Stumpfs mit $E(3|0| 4)$ , $F(3|3| 4), G(0|3| 4)$ und $H(0|0| 4)$ sind quadratisch.

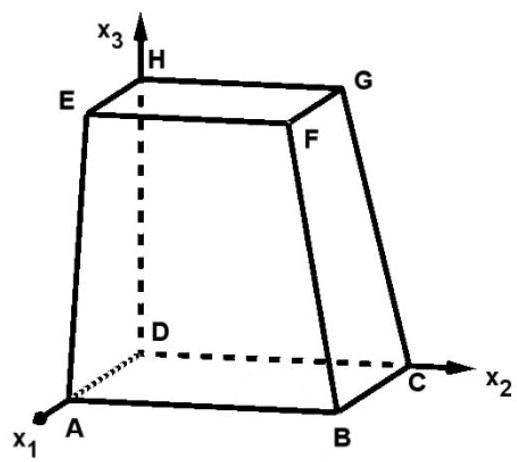
Berechnen Sie
- die Länge der Strecke $\overline{D F}$
- die Koordinaten des Mittelpunktes der Strecke $\overline{D F}$ .
(3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Länge der Strecke $\overline{D F}$
Der Vektor $\overrightarrow{DF}=\overrightarrow{OF}-\overrightarrow{OD}=\begin{pmatrix}3\\3\\4\end{pmatrix}-\begin{pmatrix}0\\0\\0\end{pmatrix}=\begin{pmatrix}3\\3\\4\end{pmatrix}$
$\left|\begin{pmatrix}3\\3\\4\end{pmatrix}\right|=\sqrt{3^2+3^2+4^2}=\sqrt{34}$
Die Länge der Strecke $\overline{D F}$ beträgt $\sqrt{34}$ .
Koordinaten des Mittelpunktes der Strecke $\overline{D F}$
$\vec m=\dfrac{1}{2}\cdot\overrightarrow{DF}=\dfrac{1}{2}\cdot\begin{pmatrix}3\\3\\4\end{pmatrix}=\begin{pmatrix}1{,}5\\1{,}5\\2\end{pmatrix}\;\Rightarrow\;M(1{,}5|1{,}5|2)$
Die Koordinaten des Mittelpunktes der Strecke $\overline{D F}$ sind $M(1{,}5|1{,}5|2)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil 1
Gib den Vektor $\overrightarrow{DF}$ an und berechne seine Länge.
Teil 2
Der Vektor, der zur Mitte zwischen zwei Punkten $A$ und $B$ zeigt, ist $\vec m=\dfrac{1}{2}\cdot\left(\overrightarrow{OA}+\overrightarrow{OB}\right)$
Erläutern Sie den folgenden Ansatz zur Berechnung der Koordinaten der Pyramidenspitze $S(0|0| 16)$ :
$\begin{pmatrix}4\\0\\0\end{pmatrix}+r\cdot \begin{pmatrix}-1\\0\\4\end{pmatrix}=\begin{pmatrix}0\\0\\s\end{pmatrix}$
(3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie
Ansatz zur Berechnung der Koordinaten der Pyramidenspitze $S(0|0| 16)$
Die Punkte $A$ und $E$ liegen auf der Geraden:
$g_{AE}:\;\vec x=\overrightarrow{OA}+r\cdot(\overrightarrow{OE}-\overrightarrow{OA})=\begin{pmatrix}4\\0\\0\end{pmatrix}+r\cdot\left(\begin{pmatrix}3\\0\\4\end{pmatrix}-\begin{pmatrix}4\\0\\0\end{pmatrix}\right)$
$g_{AE}:\;\vec x=\begin{pmatrix}4\\0\\0\end{pmatrix}+r\cdot\begin{pmatrix}-1\\0\\4\end{pmatrix}$
Die Punkte $D$ und $H$ liegen auf der $x_3$ -Achse. Hier muss auch der Punkt $S$ liegen.
$\Rightarrow\;S(0|0|s)$
Der Wert von $s$ ist die $x_3$ -Koordinate von S.
Weiterhin muss $S$ auch auf der Geraden $g$ liegen.
Damit folgt der Ansatz zur Berechnung der Pyramidenspitze:
$\begin{pmatrix}4\\0\\0\end{pmatrix}+r\cdot\begin{pmatrix}-1\\0\\4\end{pmatrix}=\begin{pmatrix}0\\0\\s\end{pmatrix}$
Mit diesem Ansatz werden die Koordinaten der Pyramidenspitze berechnet.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Punkte $A$ , $E$ und $S$ liegen auf einer Geraden.
Die Punkte $D$ und $H$ liegen auf der $x_3$ -Achse. Hier muss auch der Punkt $S$ liegen.
Bestimmen Sie das Volumen des Stumpfs. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Volumen des Stumpfs
Für das Volumen eines Pyramidenstumpfes gilt:
$V_{\text{Stumpf}}=\dfrac{h}{3}\cdot(A_G+\sqrt{A_G \cdot A_D}+A_D)$
Die $x_3$ -Koordinate des Punktes $H$ ist $4\;\Rightarrow\;h=4$
$A_G=4^2$ und $A_D=3^2$
$\Rightarrow\;V_{\text{Stumpf}}=\dfrac{4}{3}\cdot(16+\sqrt{16 \cdot 9}+9)=\dfrac{4}{3}\cdot(25+4\cdot 3)=\dfrac{148}{3}$
Das Volumen des Stumpfs beträgt $\dfrac{148}{3}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für das Volumen eines Pyramidenstumpfes gilt: $V_{\text{Stumpf}}=\dfrac{h}{3}\cdot(A_G+\sqrt{A_G \cdot A_D}+A_D)$ ; $G$ steht für Grundfläche und $D$ für Dachfläche
Alternativ kann das Stumpfvolumen auch so berechnet werden: $V_{\text{Stumpf}}=V_{\text{große Pyramide}}-V_{\text{Spitze}}$
Der Pyramidenstumpf wird soweit um die Kante $\overline{C D}$ gedreht bis die Fläche $C G H D$ in der $x_{1} x_{2}$ -Ebene liegt.
Geben Sie die Koordinaten eines Bildpunktes $H^{\prime}$ an. (2BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung mittels Matrizen
Koordinaten eines Bildpunktes $H^{\prime}$ angeben
Die Drehung des Punktes $H$ kann mit einer Drehmatrix berechnet werden.
Der Drehwinkel ist entweder $\alpha =90^\circ$ oder $\alpha =-90^\circ$ .
Die Abbildungsgleichung für eine Drehung um die y-Achse ist dann:
$\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\alpha}&0& \sin{\alpha}\\0&1&0\\-\sin{\alpha} &0& \cos{\alpha}\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}$
Mit $\alpha =90^\circ$ folgt dann:
$\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}0&0&1 \\0&1&0\\-1 &0& 0\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}$
Für den Punkt $H(4|0|0)$ erhält man den gedrehten Punkt $H'$ :
$\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}0&0&1 \\0&1&0\\-1 &0& 0\end{pmatrix}\cdot\begin{pmatrix}0\\0\\4\end{pmatrix}=\begin{pmatrix}4\\0\\0\end{pmatrix}$
Der Punkt $H'$ hat die Koordinaten $H'(4|0|0)$ .
Eine zweite Lösung erhält man für $\alpha =-90^\circ$ . Dann hat der Punkt $H'$ die Koordinaten $H'(-4|0|0)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Der Drehwinkel ist entweder $\alpha =90^\circ$ oder $\alpha =-90^\circ$ .
Die Abbildungsgleichung für eine Drehung um die y-Achse ist dann: $\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\alpha}&0& \sin{\alpha}\\0&1&0\\-\sin{\alpha} &0& \cos{\alpha}\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}$

Der Mittelpunkt $M$ der Kante $\overline{A B}$ und der Mittelpunkt $N$ der Kante $\overline{C G}$ liegen auf der Gerade $\def\arraystretch{1.25} j: \vec{x}=\left(\begin{array}{l}4 \\ 2 \\ 0\end{array}\right)+t \cdot\left(\begin{array}{c}-8 \\ 3 \\ 4\end{array}\right)$ mit $t \in \mathbb{R}$ .

Die Punkte der Kante $\overline{B C}$ lassen sich in der Form $P_{W}(w|4| 0)$ darstellen.

Für einen Punkt $P_{W}$ der Kante $\overline{B C}$ schneidet die Gerade durch $H$ und $P_{W}$ die Gerade $j$ .

Berechnen Sie den zugehörigen Wert von $w$ . (4BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung in der analytischen Geometrie

Wert von $w$

Erstelle die Gleichung der Geraden $g_{HP_w}$ durch die Punkte $H(0|0|4)$ und $P_w(w|4|0)$ :

$g_{HP_w}:\;\vec x=\overrightarrow{OH}+r\cdot(\overrightarrow{OP_w}-\overrightarrow{OH})=\begin{pmatrix}0\\0\\4\end{pmatrix}+r\cdot\left(\begin{pmatrix}w\\4\\0\end{pmatrix}-\begin{pmatrix}0\\0\\4\end{pmatrix}\right)$

$g_{HP_w}:\;\vec x=\begin{pmatrix}0\\0\\4\end{pmatrix}+r\cdot\begin{pmatrix}w\\4\\-4\end{pmatrix}$

Schneide $g_{HP_w}$ mit $j$ :

\def\arraystretch{1.25} \displaystyle \left(\begin{array}{l}4 \\ 2 \\ 0\end{array}\right)+t \cdot\left(\begin{array}{c}-8 \\ 3 \\ 4\end{array}\right)

=

\displaystyle \begin{pmatrix}0\\0\\4\end{pmatrix}+r\cdot\begin{pmatrix}w\\4\\-4\end{pmatrix}

$\mathrm{(II)}:\;2+3t=4r$

$\mathrm{(III)}:\;\;\;\;\;\;4t=4-4r$

Rechne:

$\mathrm{(II)}+\mathrm{(III)}\;\Rightarrow\;2+7t=4\;\Rightarrow\;t=\dfrac{2}{7}$

Setze $t=\dfrac{2}{7}$ in $\mathrm{(II)}$ ein:

$2+3\cdot \dfrac{2}{7}=4r\;\Rightarrow\;\dfrac{20}{7}=4r\;\Rightarrow\;r=\dfrac{5}{7}$

Setze $t=\dfrac{2}{7}$ und $r= \dfrac{5}{7}$ in $\mathrm{(I)}$ ein:

$4-8\cdot \dfrac{2}{7}=\dfrac{5}{7}\cdot w\;\Rightarrow\;\dfrac{28-16}{7}=\dfrac{5}{7}\cdot w\;\Rightarrow\;w=\dfrac{12}{5}$

Für $w=\dfrac{12}{5}$ schneidet die Gerade durch $H$ und $P_{\frac{5}{7}}$ die Gerade $j$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Es gibt Punkte $P_{W}$ der Kante $\overline{B C}$ , für die der von den Strecken $\overline{P_{W} M}$ und $\overline{P_{W} H}$ eingeschlossene Winkel größer als $70^{\circ}$ ist.

Ermitteln Sie die zugehörigen Werte von $w$ . (5BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen

Werte von $w$

Der Mittelpunkt $M$ der Kante $\overline{A B}$ hat die Koordinaten $M(4|2|0)$ .

$\vec m=\dfrac{1}{2}\cdot\left(\overrightarrow{OA}+\overrightarrow{OA}\right)=\dfrac{1}{2}\cdot \left(\begin{pmatrix}4\\0\\0\end{pmatrix}+\begin{pmatrix}4\\4\\0\end{pmatrix}\right)=\begin{pmatrix}4\\2\\0\end{pmatrix}\;\Rightarrow\;M(4|2|0)$

Der Vektor $\overrightarrow{P_wM}=\begin{pmatrix}4\\2\\0\end{pmatrix}-\begin{pmatrix}w\\4\\0\end{pmatrix}=\begin{pmatrix}4-w\\-2\\0\end{pmatrix}$ .

Der zweite Vektor ist $\overrightarrow{P_wH}=\begin{pmatrix}0\\0\\4\end{pmatrix}-\begin{pmatrix}w\\4\\0\end{pmatrix}=\begin{pmatrix}-w\\-4\\4\end{pmatrix}$

Der eingeschlossene Winkel zwischen den beiden Vektoren soll größer als $70^{\circ}$ sein.

Für den Winkel $70^\circ$ zwischen den beiden Vektoren gilt:

$\cos70^{\circ}=\dfrac{\overrightarrow{P_wM}\circ\overrightarrow{P_wM}}{\left|\overrightarrow{P_wM}\right|\cdot \left|\overrightarrow{P_wH}\right|}$

Mit $\left|\overrightarrow{P_wM}\right|=\sqrt{(4-w)^2+(-2)^2+0^2}=\sqrt{(4-w)^2+4}$ und $\left|\overrightarrow{P_wH}\right|=\sqrt{(-w)^2+(-4)^2+4^2}=\sqrt{w^2+32}$ folgt dann:

$\displaystyle \cos70^{\circ}$	$=$	$\displaystyle \dfrac{\begin{pmatrix}4-w\\-2\\0\end{pmatrix}\circ\begin{pmatrix}-w\\-4\\4\end{pmatrix}}{\sqrt{(4-w)^2+4}\cdot \sqrt{w^2+32}}$
	$=$	$\displaystyle \dfrac{(4-w)\cdot(-w)+(-2)\cdot(-4)+0}{\sqrt{((4-w)^2+4)\cdot (w^2+32)}}$
	$=$	$\displaystyle \dfrac{w^2-4w+8}{\sqrt{((4-w)^2+4)\cdot(w^2+32)}}$

Der Winkel $\alpha = 70^{\circ}$ ist im Bogenmaß gleich $\dfrac{7}{18}\cdot \pi$ .

Löse die Gleichung $\cos\left(\dfrac{7\cdot \pi}{18}\right)=\dfrac{w^2-4w+8}{\sqrt{((4-w)^2+4)\cdot(w^2+32)}}$

Der GTR liefert als Lösung dieser Gleichung $w_1\approx2{,}960314051$ .

$\Rightarrow\;w_1\approx2{,}96$

Es ist $P_w(w|4|0)$ .

Für $w=0$ ist $P_w(0|4|0)=C$ und für $w=4$ ist $P_w(4|4|0)=B$ .

$P_w$ liegt dann auf $\overline{B C}$ , wenn $0\leq w\leq 4$ gilt.

Für $w=4$ erhält man für den eingeschlossenen Winkel:

$\cos\alpha=\dfrac{(4-4)\cdot(-4)+(-2)\cdot(-4)+0}{\sqrt{((4-4)^2+4)\cdot (4^2+32)}}=\dfrac{8}{\sqrt{4\cdot 48}}=\dfrac{8}{\sqrt{}192}$

$\alpha=\cos^{-1}\left(\dfrac{8}{\sqrt{192}}\right)\approx54{,}7^\circ$

Der eingeschlossenen Winkel ist also kleiner als $70^\circ$ .

Also ist der Winkel für $0\leq w< w_1$ größer als $70^\circ$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

9

Aufgabe 3C

Die Abbildung zeigt modellhaft das Dach eines Kirchturms.

Die Eckpunkte der dreieckigen Giebelflächen (grau markiert) und der viereckigen Dachflächen werden durch die Punkte $B(8|0| 0), C(8|8| 0), E(4|0| 6), F(8|4| 6), G(4|8| 6)$ und $S(4|4| 12)$ sowie $A, D$ und $H$ dargestellt.

Die vier Dachflächen haben die gleiche Form und die gleiche Größe. Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Realität.

Die Materialstärken der Bauteile des Dachs sollen im Folgenden vernachlässigt werden.

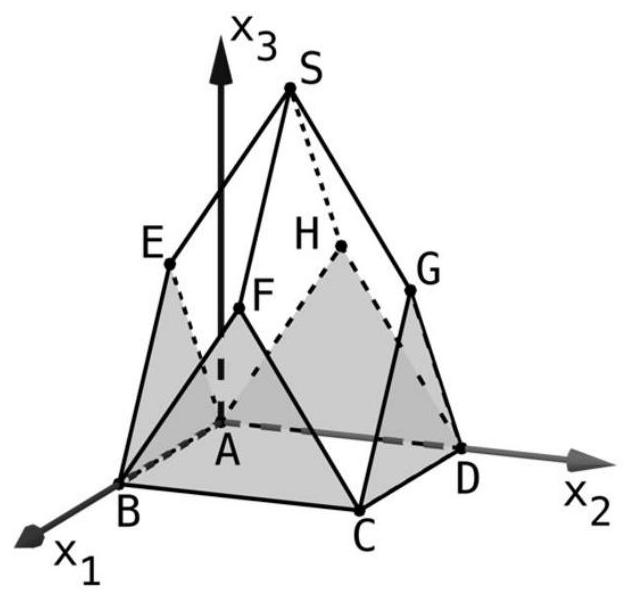
Die Ebene $L$ enthält die Punkte $C, G$ und $F$ .

Geben Sie eine Gleichung von $L$ in Parameterform an und zeigen Sie, dass auch $S$ in $L$ liegt. (4BE)

Weisen Sie nach, dass das Viereck $CGSF$ eine Raute ist. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Das Viereck $CGSF$ ist eine Raute
Eine Raute ist ein Viereck, bei dem alle vier Seiten gleich lang sind.
$\overrightarrow{CF}=\begin{pmatrix}0\\-4\\6\end{pmatrix}\;\Rightarrow\;\left|\overrightarrow{CF}\right|=\sqrt{0^2+(-4)^2+6^2}=\sqrt{52}$
$\overrightarrow{CG}=\begin{pmatrix}-4\\0\\6\end{pmatrix}\;\Rightarrow\;\left|\overrightarrow{CG}\right|=\sqrt{(-4)^2+0^2+6^2}=\sqrt{52}$
$\overrightarrow{FS}=\left(\begin{pmatrix}4\\4\\12\end{pmatrix}-\begin{pmatrix}8\\4\\6\end{pmatrix}\right)=\begin{pmatrix}-4\\0\\6\end{pmatrix}=\overrightarrow{CG}$
$\overrightarrow{GS}=\left(\begin{pmatrix}4\\4\\12\end{pmatrix}-\begin{pmatrix}4\\8\\6\end{pmatrix}\right)=\begin{pmatrix}0\\-4\\6\end{pmatrix}=\overrightarrow{CF}$
Also sind alle 4 Seiten gleich lang und das Viereck $CGSF$ ist eine Raute.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Eine Raute ist ein Viereck, bei dem alle vier Seiten gleich lang sind. Berechne die entsprechenden Seitenlängen.

Berechnen Sie die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$ sowie den gesamten Flächeninhalt der Dachflächen. (5BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen Vektoren, Geraden und Ebenen

Die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$

Für den Winkel zwischen den Vektoren $\overrightarrow{SF}$ und $\overrightarrow{SG}$ gilt:

$\cos \varphi=\left(\dfrac{\overrightarrow{SF} \circ\overrightarrow {SG}}{\left|\overrightarrow {SF}\right|\cdot\left|\overrightarrow {SG}\right|}\right)$

Dabei ist $\overrightarrow{SF}=\begin{pmatrix}4\\0\\-6\end{pmatrix}$ und $\overrightarrow{SG}=\begin{pmatrix}0\\4\\-6\end{pmatrix}$

Die Beträge der beiden Vektoren sind gleich $\sqrt{52}$ .

Dann folgt:

$\displaystyle \cos \varphi$	$=$	$\displaystyle \dfrac{\overrightarrow{SF} \circ\overrightarrow {SG}}{\left\|\overrightarrow {SF}\right\|\cdot\left\|\overrightarrow {SG}\right\|}$
	↓	Setze die bekannten Vektoren und Beträge ein.
	$=$	$\displaystyle \dfrac{\begin{pmatrix}4\\0\\-6\end{pmatrix} \circ\begin{pmatrix}0\\4\\-6\end{pmatrix}}{\sqrt{52}\cdot\sqrt{52}}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{36}{52}$

$\displaystyle \varphi=\arccos\left(\dfrac{36}{52}\right)\approx46{,}2^\circ$

Die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$ beträgt rund $46^\circ$ .

Flächeninhalt der Dachflächen

Die Dachflächen bestehen aus vier Rauten.

Der Flächeninhalt einer Raute ist die Hälfte des Produkts der Länge beider Diagonalen: $A_{Raute}=\frac12\cdot e\cdot f$

$\Rightarrow\;A_{ges}=4\cdot\dfrac{1}{2}\cdot\left|\overrightarrow{FG}\right|\cdot \left|\overrightarrow{CS}\right|$

$\overrightarrow{FG}=\begin{pmatrix}4\\8\\6\end{pmatrix}-\begin{pmatrix}8\\4\\6\end{pmatrix}=\begin{pmatrix}-4\\4\\0\end{pmatrix}$

$\left|\overrightarrow{FG}\right|=\sqrt{(-4)^2+4^2+0^2}=\sqrt{32}$

$\overrightarrow{CS}=\begin{pmatrix}4\\4\\12\end{pmatrix}-\begin{pmatrix}8\\8\\0\end{pmatrix}=\begin{pmatrix}-4\\-4\\12\end{pmatrix}$

$\left|\overrightarrow{CS}\right|=\sqrt{(-4)^2+(-4)^2+12^2}=\sqrt{176}$

Dann ist:

$A_{ges}=4\cdot\dfrac{1}{2}\cdot\sqrt{32}\cdot \sqrt{176}=2\cdot\sqrt{16\cdot 2\cdot8\cdot22}=2\cdot16\cdot\sqrt{22}=32\cdot\sqrt{22}\approx150\;\text{m}^2$

Der gesamte Flächeninhalt der Dachflächen beträgt rund $150\;\text{m}^2$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Die Gerade $q_{1}$ verläuft durch $S$ und $F$ , die Gerade $q_{2}$ durch $S$ und $G$ . Die beiden Geraden schneiden die $x_{1} x_{2}$ -Ebene in den Punkten $Q_{1}$ bzw. $Q_{2}$ .
Geben Sie das Verhältnis des Abstands von $Q_{1}$ und $Q_{2}$ zum Abstand von $F$ und $G$ an.
Begründen Sie Ihre Angabe, ohne die Koordinaten von $Q_{1}$ und $Q_{2}$ zu berechnen. (3BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strahlensatz oder Vierstreckensatz, Ähnlichkeit
Verhältnis des Abstands von $Q_{1}$ und $Q_{2}$ zum Abstand von $F$ und $G$
Die Dreiecke $SQ_1Q_2$ und $SFG$ haben bei $S$ einen gemeinsamen Innenwinkel.
Die Gerade $Q_1Q_2$ ist parallel zur Geraden $FG$ .
Begründung: Die Punkte $Q_1$ und $Q_2$ haben die gleichen z-Koordinaten ( $z=6$ ) und ebenso haben die Punkte $F$ und $G$ die gleichen z-Koordinaten ( $z=0$ ).
Damit sind die beiden Dreiecke ähnlich.
Die Strecke $\overline{SQ_1}$ ist doppelt so lang wie die Strecke $\overline{SF}$ , da die z-Koordinate von $S$ gleich $12$ und die z-Koordinaten von $F$ und $G$ gleich $6$ sind.
Folglich ist der Abstand von $Q_1$ und $Q_2$ doppelt so groß wie der Abstand von $F$ und $G$ .
Die folgende Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Welche Beziehung besteht zwischen den Dreiecken $SQ_1Q_2$ und $SFG$ ?
Finde einen Zusammenhang zwischen den beiden Strecken $\overline{SQ_1}$ und $\overline{SF}$ .
Zur Stabilisierung wird zwischen den durch $E$ und $G$ dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch $\overline{S F}$ dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, wird im Modell mit $R$ bezeichnet.
Berechnen Sie die Koordinaten von $R$ . (5BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Koordinaten von $R$
Die Mitte der Strecke $\overline{EG}$ ist der Punkt $M$ .
$\vec m =\dfrac{1}{2}\cdot\left(\overrightarrow{OE}+\overrightarrow{OG}\right)=\dfrac{1}{2}\cdot\left(\begin{pmatrix}4\\0\\6\end{pmatrix}+\begin{pmatrix}4\\8\\6\end{pmatrix}\right)=\begin{pmatrix}4\\4\\6\end{pmatrix}$
Der Punkt $M$ hat die Koordinaten $M(4|4|6)$ .
Für den Vektor $\overrightarrow{OR}$ gilt:
$\overrightarrow{OR}=\overrightarrow{OS}+t\cdot \overrightarrow{SF}$
Weiterhin muss gelten (kürzester Abstand):
$\left(\overrightarrow{OR}-\overrightarrow{OM}\right)\circ\overrightarrow{SF}=0\;\Rightarrow\;\left(\overrightarrow{OS}+t\cdot \overrightarrow{SF}-\overrightarrow{OM}\right)\circ\overrightarrow{SF}=0$
$\Rightarrow\;\left(\begin{pmatrix}4\\4\\12\end{pmatrix}+t\cdot \begin{pmatrix}4\\0\\-6\end{pmatrix}-\begin{pmatrix}4\\4\\6\end{pmatrix}\right)\circ \begin{pmatrix}4\\0\\-6\end{pmatrix}=0$
Vektoren zusammenfassen:
$\Rightarrow\;\left(\begin{pmatrix}0\\0\\6\end{pmatrix}+t\cdot \begin{pmatrix}4\\0\\-6\end{pmatrix}\right)\circ \begin{pmatrix}4\\0\\-6\end{pmatrix}=0$
Skalarprodukt berechnen:
$-36+t\cdot(16+36)=0\;\Rightarrow\;t=\dfrac{36}{52}=\dfrac{9}{13}$
Mit $t=\dfrac{9}{13}$ erhält man die Koordinaten des Punktes $R$ :
$\overrightarrow{OR}=\begin{pmatrix}4\\4\\12\end{pmatrix}+\dfrac{9}{13}\cdot \begin{pmatrix}4\\0\\-6\end{pmatrix}=\begin{pmatrix}4+\frac{36}{13}\\4+0\\12-\frac{54}{13}\end{pmatrix}=\begin{pmatrix}\frac{88}{13}\\4\\\frac{102}{13}\end{pmatrix}$
Die Koordinaten des Punktes $R$ lauten $R\left(\frac{88}{13}|4|\frac{102}{13}\right)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Mitte der Strecke $\overline{EG}$ ist der Punkt $M$ . Berechne $M$ .
Für den Vektor $\overrightarrow{OR}$ gilt: $\overrightarrow{OR}=\overrightarrow{OS}+t\cdot \overrightarrow{SF}$
Weiterhin steht der Vektor $\overrightarrow{OR}-\overrightarrow{OM}$ senkrecht auf dem Vektor $\overrightarrow{SF}$ . Löse die dazugehörende Gleichung nach $t$ auf und berechne dann die Koordinaten des Punktes $R$ .

$\displaystyle 0{,}7$	$=$	$\displaystyle 0{,}9\cdot (1-x)$	$\displaystyle :0{,}9$
$\displaystyle \dfrac{0{,}7}{0{,}9}$	$=$	$\displaystyle 1-x$	$\displaystyle +x$
$\displaystyle \dfrac{0{,}7}{0{,}9}+x$	$=$	$\displaystyle 1$	$\displaystyle -\dfrac{0{,}7}{0{,}9}$
$\displaystyle x$	$=$	$\displaystyle 1-\dfrac{7}{9}$
	$=$	$\displaystyle \dfrac{2}{9}$

$\displaystyle \begin{pmatrix}4\\4\\12\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix}8\\8\\0\end{pmatrix}+r\cdot\begin{pmatrix}0\\-4\\6\end{pmatrix}+s\cdot \begin{pmatrix}-4\\0\\6\end{pmatrix}$	$\displaystyle -\begin{pmatrix}8\\8\\0\end{pmatrix}$
$\displaystyle \begin{pmatrix}-4\\-4\\12\end{pmatrix}$	$=$	$\displaystyle r\cdot\begin{pmatrix}0\\-4\\6\end{pmatrix}+s\cdot \begin{pmatrix}-4\\0\\6\end{pmatrix}$

Wahlteil - GTR

Aufgabe 1A

Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht

Größter Wert

Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören

Hast du eine Frage oder Feedback?

Erläuterung zu den Berechnungen

Die beiden Zeitpunkte

Hast du eine Frage oder Feedback?

Vergleich der momentanen Änderungsraten

Hast du eine Frage oder Feedback?

Anzahl der im ersten Jahr verkauften Smartwatches

Zeitpunkt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden

Hast du eine Frage oder Feedback?

Koordinaten des Extrempunktes und des Wendepunktes

Hast du eine Frage oder Feedback?

Tangentengleichung aufstellen

Nullstelle der Tangente und Integrationsgrenze für später

Flächeninhalte bestimmen

Hast du eine Frage oder Feedback?

Gleichungen der beiden Ursprungsgeraden

Hast du eine Frage oder Feedback?

Begründung

Visualisierung

Hast du eine Frage oder Feedback?

Aufgabe 1B

Die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben

Hast du eine Frage oder Feedback?

Verfahren zur Bestimmung einer Funktion

Drei Schritte der Durchführung des Verfahrens

Hast du eine Frage oder Feedback?

Zeichnung des Graphen von fff

Hast du eine Frage oder Feedback?

Jährliche prozentuale Zunahme der Schulden

Zeitpunkt, zu dem die momentane Änderungsrate der Schulden größer als 250250250 Mrd. Euro pro Jahr ist

Hast du eine Frage oder Feedback?

Das Jahr, in dem die Schulden ihren Höchststand erreichen

Hast du eine Frage oder Feedback?

Begründung, dass sich die zu erwartenden Schulden zu Beginn des Jahres 2005+m2005+m2005+m mithilfe des folgenden Terms berechnen lassen: 1490+∫0mg(x) dx1490+\displaystyle\int_{0}^{m} g(x)\; d x1490+∫0m​g(x)dx

Das Jahr, in dem die Schulden vollständig abgebaut sind

Hast du eine Frage oder Feedback?

Zeitraum bestimmen

Hast du eine Frage oder Feedback?

Aufgabe 1C

Nachweis der Tangente

Hast du eine Frage oder Feedback?

Veranschaulichung der Graphen

I. Die Funktion fff ist überall monoton steigend.

II. An der Stelle x=6x=6x=6 hat die Funktion fff kein lokales Maximum.

III. Die Tangente an den Graphen von fff im Punkt (0,5∣f(0,5))(0{,}5 \mid f(0{,}5))(0,5∣f(0,5)) ist parallel zu zwei weiteren Tangenten an den Graphen von fff

Hast du eine Frage oder Feedback?

Die Symmetrie des Graphen von f′f^{\prime}f′

Begründung ausgehend vom Graphen von hhh

Hast du eine Frage oder Feedback?

Kann ein Wohnmobil mit einer Länge von 7,057{,}057,05 m und einer Höhe von 3,10 m3{,}10 \mathrm{~m}3,10 m vollständig im Carport untergestellt werden?

Hast du eine Frage oder Feedback?

Untersuche, ob die maximale Neigung des Carportdachs höchstens 25 %25\;\%25% beträgt

Hast du eine Frage oder Feedback?

Der Inhalt der verkleideten Fläche

Hast du eine Frage oder Feedback?

Die xxx-Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt

Hast du eine Frage oder Feedback?

Aufgabe 2A

Genau neun Pakete haben das Ziel B

Weniger als neun Pakete haben das Ziel B

Hast du eine Frage oder Feedback?

Prozentuale Abweichung der Anzahl vom Erwartungswert

Hast du eine Frage oder Feedback?

Anteil der Pakete mit dem Ziel C\mathrm{C}C unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden

Hast du eine Frage oder Feedback?

Geben Sie ein passendes Ereignis an

Hast du eine Frage oder Feedback?

Ist der Anteil der Pakete mit Ziel AAA unter den schweren Paketen ebenso groß ist wie unter den nicht-schweren Paketen?

Hast du eine Frage oder Feedback?

Anteil der schweren Pakete unter denen, die weder Ziel A noch Ziel B haben

Hast du eine Frage oder Feedback?

Aufgabe 2B

Nur runde Bälle sind in der Stichprobe enthalten

Die Stichprobe mindestens 190190190 runde Bälle enthält

Die Stichprobe genau einen oder genau zwei unrunde Bälle enthält

Zeichnung des Graphen von $f$

Zeitpunkt, zu dem die momentane Änderungsrate der Schulden größer als $250$ Mrd. Euro pro Jahr ist

Begründung, dass sich die zu erwartenden Schulden zu Beginn des Jahres $2005+m$ mithilfe des folgenden Terms berechnen lassen: $1490+\displaystyle\int_{0}^{m} g(x)\; d x$

I. Die Funktion $f$ ist überall monoton steigend.

II. An der Stelle $x=6$ hat die Funktion $f$ kein lokales Maximum.

III. Die Tangente an den Graphen von $f$ im Punkt $(0{,}5 \mid f(0{,}5))$ ist parallel zu zwei weiteren Tangenten an den Graphen von $f$

Die Symmetrie des Graphen von $f^{\prime}$

Begründung ausgehend vom Graphen von $h$

Kann ein Wohnmobil mit einer Länge von $7{,}05$ m und einer Höhe von $3{,}10 \mathrm{~m}$ vollständig im Carport untergestellt werden?

Untersuche, ob die maximale Neigung des Carportdachs höchstens $25\;\%$ beträgt

Die $x$ -Koordinate des Punkts, der den Endpunkt der zweiten Stütze am Dach darstellt

Anteil der Pakete mit dem Ziel $\mathrm{C}$ unter allen Paketen, die pro Jahr im Paketzentrum angeliefert werden

Ist der Anteil der Pakete mit Ziel $A$ unter den schweren Paketen ebenso groß ist wie unter den nicht-schweren Paketen?

Die Stichprobe mindestens $190$ runde Bälle enthält

Bedeutung des Terms $0{,}98 \cdot 0{,}05 \cdot 2000$ im Sachzusammenhang

Nachweis der Wahrscheinlichkeit: $0{,}02 \cdot 0{,}1^{2}$

Das größte Gewicht an, das ein zufällig ausgewählter Ball mit einer Wahrscheinlichkeit von höchstens $20\;\%$ unterschreitet

Wahrscheinlichkeit, dass in einer Stichprobe von $24$ zufällig ausgewählten Bällen höchstens einer ein Gewicht aufweist, das kleiner als $2{,}67$ g oder größer als $2{,}77$ g ist

Ermitteln Sie den im Baumdiagramm genannten Anteil $x$

Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Elektroauto des Herstellers das Merkmal $B$ aufweist

Ermitteln Sie, wie viele Autos mit dem Merkmal $A$ sich unter diesen zehn Autos mindestens befinden müssen, damit mit einer Wahrscheinlichkeit von mindestens $90\; \%$ von den ersten drei betrachteten Autos mindestens eines das Merkmal $A$ aufweist

Länge der Strecke $\overline{D F}$

Koordinaten des Mittelpunktes der Strecke $\overline{D F}$

Ansatz zur Berechnung der Koordinaten der Pyramidenspitze $S(0|0| 16)$

Koordinaten eines Bildpunktes $H^{\prime}$ angeben

Wert von $w$

Werte von $w$

Gleichung von $L$ in Parameterform

Nachweis, dass auch $S$ in $L$ liegt

Das Viereck $CGSF$ ist eine Raute

Die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$

Verhältnis des Abstands von $Q_{1}$ und $Q_{2}$ zum Abstand von $F$ und $G$

Koordinaten von $R$