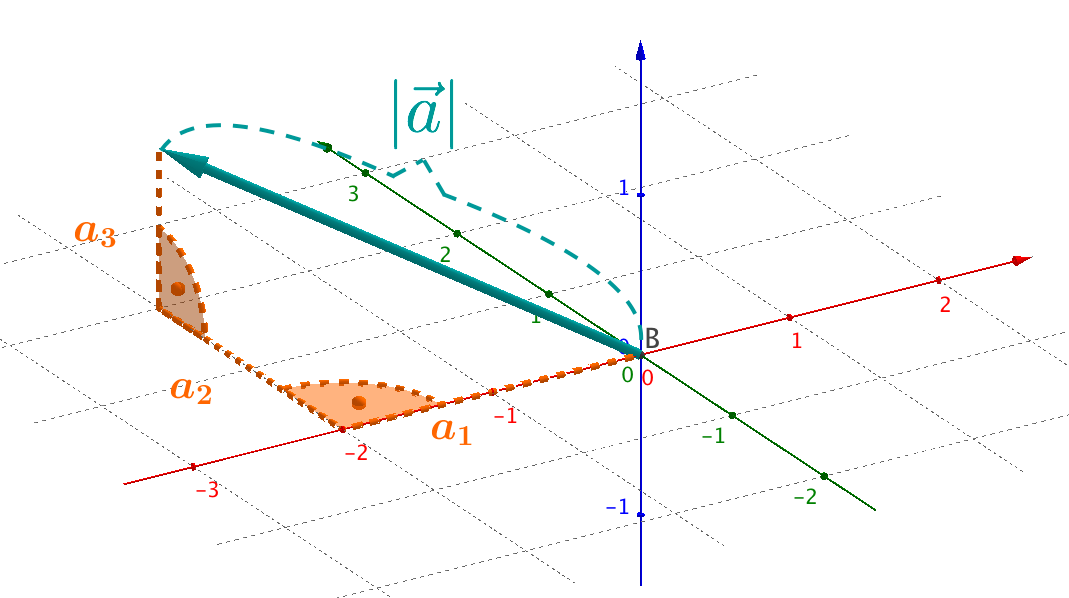
Stellt man sich einen Vektor als einen Pfeil vor, so bezeichnet man als seinen Betrag die Länge der Strecke vom Fuß bis zur Spitze. Man spricht daher auch oft von der Länge des Vektors.
Notation: Für den Betrag eines Vektors benutzt man das Symbol . In vielen Büchern findet man auch die Schreibweise .

Vektor und seine Länge
Berechnung
Der Betrag eines Vektors wird durch den Satz des Pythagoras berechnet. Die einzelnen Koordinaten werden dabei quadriert und addiert, dann wird aus dem Ergebnis die Wurzel gezogen.
In der Ebene
Für ist die Länge von :

Der Betrag eines Vektors ist auch gleich der Wurzel aus dem Skalarprodukt des Vektors mit sich selbst, also
Im Raum
Für ist die Länge von :
Der Betrag eines Vektors ist auch gleich der Wurzel aus dem Skalarprodukt des Vektors mit sich selbst, also
Beispiele
Die Länge beider Vektoren und ist gleich .
Die Länge des Vektors ist .
Bezug zum Betrag von reellen Zahlen
Wie der Betrag einer reellen Zahl, kann auch der Betrag eines Vektors als der Abstand des Vektors "zur Null" (also zum Ursprung) verstanden werden. Daher benutzt man das Symbol für die Länge des Vektors .
Wie bei den reellen Zahlen gilt:
Die Vektoren und haben immer den gleichen Betrag.
Der Betrag von einem Vielfachen von ist gleich dem Betrag der reellen Zahl (!) , mal den Betrag des Vektors .
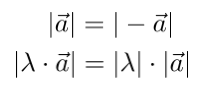
Anwendungen
Vektoren spielen in vielen Aspekten des realen Lebens eine Rolle. So lassen sich zum Beispiel
Flugbahnen von Flugzeugen und Planeten, sowie
physikalische Kräfte wie die Schwerkraft oder ein Magnetfeld
mithilfe von Vektoren beschreiben.
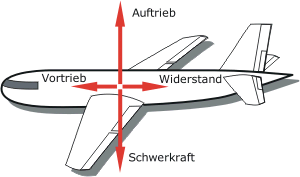
Auf ein Flugzeug wirkende Kräfte
Die Länge der Vektoren, beschreibt dann
die Geschwindigkeit eines Flugzeugs (oder eines Planeten) zu einem gewissen Zeitpunkt, oder auch
das Gewicht eines Objekts (oder die Stärke eines Magnetfeldes)
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Länge eines Vektors
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
