Teil 2 Lineare Algebra und analytische Geometrie I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In einer Kletterhalle für Kinder soll eine Wand mit Überhang gebaut werden, welche modellhaft in einem geeignet gewählten kartesischen Koordinatensystem des $ℝ^{3}$ betrachtet wird. Der Boden der Kletterhalle liegt in der $x_{1} - x_{2}$ -Koordinatenebene. Die Ebene $G$ , die den Überhang bildet, ist durch die Punkte $E (15 | 0 | 5)$ , $C (12 | 9 | 12)$ und $D (- 1 | 9 | 12)$ festgelegt. Zudem sind die Punkte $A (15 | 0 | 25)$ , $B (- 11 | 0 | 25)$ und $F (- 2 | 0 | 5)$ gegeben. Die Koordinaten der Punkte sind Längenangaben in der Einheit Dezimeter.
Auf die Mitführung von Einheiten während der Rechnung kann verzichtet werden. Ergebnisse sind gegebenenfalls auf eine Nachkommastelle zu runden.
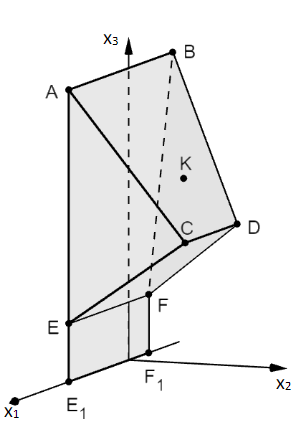
1. Bestimmen Sie eine Gleichung der Ebene $G$ in Koordinatenform und beschreiben Sie die besondere Lage von $G$ im Koordinatensystem.
  [Mögliches Ergebnis: $G$ : $7 x_{2} - 9 x_{3} + 45 = 0$ ]
2. Berechnen Sie den Neigungswinkel der Ebene $G$ zum Boden.
3. Berechnen Sie die Maßzahl des Flächeninhalts des dreieckigen Seitenteils $A E C .$
4. Die Decke der Halle, an der eine Überwachungskamera angebracht werden soll, liegt in der Ebene $H : x_{3} - 26 = 0$ . Um alle Bereiche der Kletterwand zu erfassen, muss die Kamera weit genug von der Rückwand $A E_{1} F_{1} B$ entfernt sein. Bestimmen Sie eine Gleichung der Schnittgeraden $s$ der Ebene $G$ und der Ebene $H$ . Der Abstand dieser Schnittgeraden $s$ zur $x_{1}$ - $x_{3}$ -Koordinatenebene entspricht dem Mindestabstand der Kamera von der Rückwand $A E_{1} F_{1} B$ in Dezimeter. Geben Sie diesen Abstand an.
5. Der Punkt $K$ ist der Schnittpunkt der beiden Diagonalen des Vierecks $A C D B$ . Zur Stabilisierung wird innerhalb der Kletterwand ein Stahlträger am Punkt $K$ angebracht, der senkrecht zur Kletterfläche $A C D B$ steht. Beschreiben Sie, wie der Montagepunkt des Stahlträgers an der Rückwand $A E_{1} F_{1} B$ ermittelt werden kann, ohne die Rechnung durchzuführen.
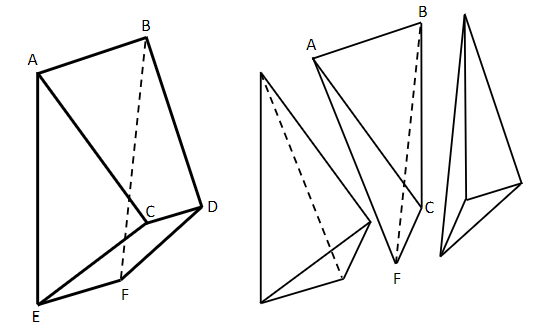
6. Der Körper $A B C D E F$ kann in drei Teilkörper zerlegt werden (siehe Skizze). Berechnen Sie die Maßzahl des Volumens der dreiseitigen Pyramide $A B C F$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?