B2 - lernen mit Serlo!

Aufgabe 5

Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.

Zur Modellierung der oberen Randlinie von Element E2 verwendet das Architekturbüro für $-4 \leq x \leq 4{,}8$ die Funktion $f$ mit $f(x)=-\frac{1}{256} x^{4}+\frac{1}{8} x^{2}+1{,}2, \quad x \in \mathbb{R}$ .

Dabei entspricht eine Längeneinheit im Koordinatensystem $1\;\mathrm{~m}$ in der Realität.

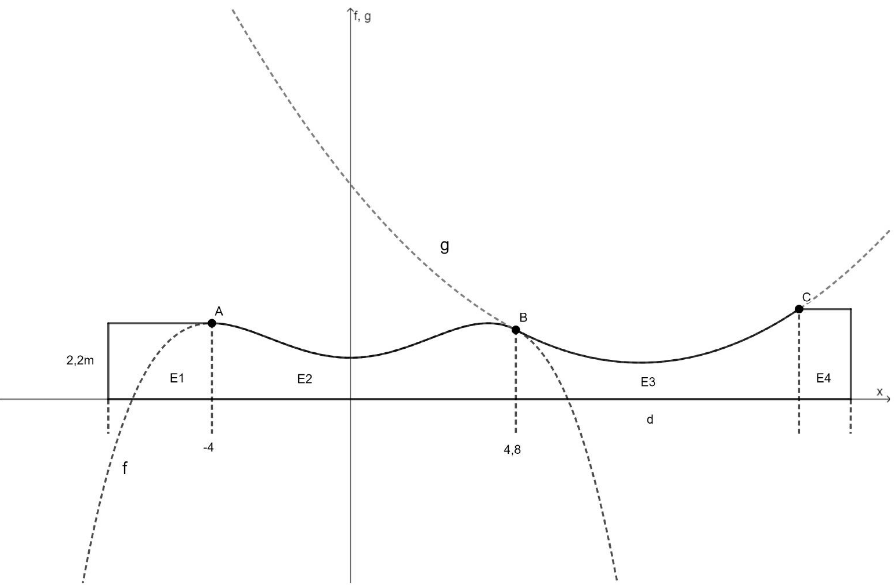
Siehe Abbildung 2:

Der Abschnitt E3 wird schließlich mit einer Länge von $d=7{,}5\mathrm{~m}$ gebaut.

Eine Kamera soll in einer Höhe von $5\mathrm{~m}$ über der unteren Randlinie von E3 befestigt werden, um die Fahrten der Skater auf E3 zu filmen. Die Position der Kamera wird vereinfacht durch den Punkt $K\left(x_{K} \mid 5\right)$ dargestellt.

Ermitteln Sie den Wert von $x_{K}$ , für den die Punkte $B$ und $C$ gleich weit von $K$ entfernt sind. (4 P)

Ermittele den Wert von $x_{K}$ , für den die Punkte $B$ und $C$ gleich weit von $K$ entfernt sind
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimmen Sie die minimale Entfernung des Punktes $K(8{,}49 \mid 5)$ vom Graphen von $g$ . (4 P)

Bestimme die minimale Entfernung des Punktes $K(8{,}49 \mid 5)$ vom Graphen von g
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen → Was bedeutet das?

Aufgabe 5

Ermittele den Wert von xKx_{K}xK​, für den die Punkte BBB und CCC gleich weit von KKK entfernt sind

Hast du eine Frage oder Feedback?

Bestimme die minimale Entfernung des Punktes K(8,49∣5)K(8{,}49 \mid 5)K(8,49∣5) vom Graphen von g

Hast du eine Frage oder Feedback?

Ermittele den Wert von $x_{K}$ , für den die Punkte $B$ und $C$ gleich weit von $K$ entfernt sind

Bestimme die minimale Entfernung des Punktes $K(8{,}49 \mid 5)$ vom Graphen von g