Teil 2 Lineare Algebra und analytische Geometrie I: mit Hilfsmitteln
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Für die Bühnenbeleuchtung einer Theateraufführung an einer Beruflichen Oberschule wird ein Scheinwerfer (siehe Bild 1) installiert. Die Position des Scheinwerfers und der von ihm ausgeleuchtete Raum auf der Bühne wird modellhaft in einem kartesischen Koordinatensystem des beschrieben. Die --Ebene des Koordinatensystems wird durch den Bühnenboden festgelegt. Die rechteckige Glasfläche des Scheinwerfers hat die Ecken , , und .
Die Vollausleuchtung mit dem Scheinwerfer ohne Berücksichtigung des Halbschattens kann in guter Näherung durch den Körper (siehe Bild 2) beschrieben werden.
Die Punkte , und sind die Eckpunkte der ausgeleuchteten Fläche auf dem Bühnenboden.
Die Koordinaten sind Längenangaben in der Einheit Dezimeter ().
Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden. Die Ergebnisse sind sinnvoll zu runden.
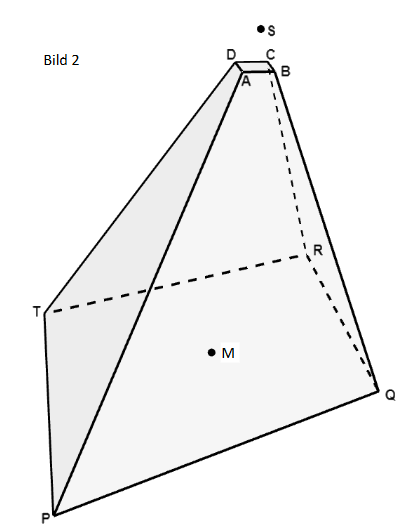
Die Gerade verläuft durch die Punkte und . Die Gerade verläuft durch die Punkte und . Die Geraden und g schneiden sich im Punkt . Berechnen Sie die Koordinaten des Punktes . [ Ergebnis: ]
(6 BE)
Stellen Sie eine Gleichung der Lotgeraden zur Ebene , in der sich die Glasfläche befindet, durch den Punkt auf und bestimmen Sie den Abstand des Punktes zur Ebene .
[ Mögliches Teilergebnis: : , ]
(8 BE)
Die Diagonalen des Vierecks schneiden sich im Punkt . (Nachweis nicht erforderlich). Zeigen Sie, dass der Punkt auf der Geraden liegt. Berechnen Sie die Größe des Schnittwinkels der Geraden mit der -- Koordinatenebene.
(4 BE)
Der Scheinwerfer besitzt einen Flügelbegrenzer (siehe Bild 3). Der einzustellende Winkel soll für den rechten Flügel berechnet werden. Vereinfachend soll angenommen werden, dass der rechte Flügel in der Ebene liegt, die durch die Punkte und festgelegt ist. Berechnen Sie die Größe des Schnittwinkels zwischen der Ebene und der Ebene .
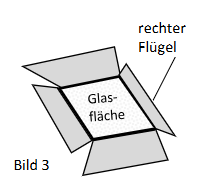
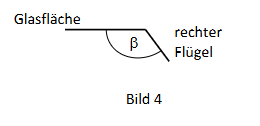
Schließen Sie anschließend auf die Größe des einzustellenden Winkels zwischen der Glasfläche des Scheinwerfers und dem rechten Flügel des Flügelbegrenzers (siehe Bild 4).
(5 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
