Teil 2 Lineare Algebra und analytische Geometrie II: mit Hilfsmitteln

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
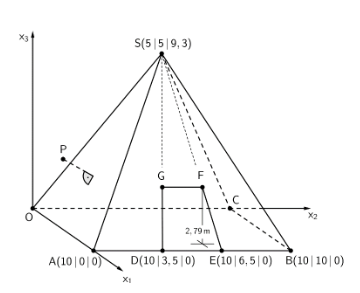
Für einen Stand auf der nächsten Reisemesse in München plant ein Veranstalter ein Zelt, das in einem kartesischen Koordinatensystem des $ℝ^{3}$ (vgl. Abbildung) modellhaft durch eine Pyramide $O A B C S$ mit quadratischer Grundfläche dargestellt wird. Die Zeltwand $O A S$ liegt in der Ebene $H : - 93 x_{2} + 50 x_{3} = 0$
Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter. Auf die Mitführung von Einheiten kann bei den Rechnungen verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.
1. Auch nach der Corona-Pandemie wird in den Zelten auf der Reisemesse auf eine
  Beschränkung der Anzahl der sich gleichzeitig im Zelt aufhaltenden Personen geachtet. Die Kenndaten der eingebauten Lüftungsanlage geben für das hier betrachtete Zelt eine Obergrenze von $0,2$ Personen pro Kubikmeter Raumvolumen vor. Ermitteln Sie, wie viele Personen sich gleichzeitig im betrachteten Zelt aufhalten dürfen.
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Ermittle, wie viele Personen sich gleichzeitig im betrachteten Zelt aufhalten dürfen
  Gegeben sind die quadratische Grundfläche mit der Kantenlänge $10 m$ und die Pyramidenhöhe $9,3 m$ (aus der Abbildung entnommen).
  $V = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot 10^{2} \cdot 9,3 = 310$
  Die Pyramide hat ein Volumen von $310 m^{3}$ .
  Personenanzahl $= 300 \cdot 0,2 = 62$
  Es dürfen sich 62 Personen gleichzeitig im betrachteten Zelt aufhalten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Gegeben sind die quadratische Grundfläche mit der Kantenlänge $a$ und die Pyramidenhöhe $h$ (die Werte können aus der Abbildung entnommen werden).
  $V = \frac{1}{3} \cdot G \cdot h \Rightarrow V_{1}$
  Personenanzahl $= V_{1} \cdot 0,2$
2. Die Zeltwände dienen als Projektionsflächen für Beamer, die außerhalb des Zelts montiert sind. Auf die Zeltwand, an der sich der Zelteingang befindet, wird nicht projiziert.
  1) Damit die Projektionen gut sichtbar sind, werden die drei Zeltwände vollständig mit einer speziellen Folie beklebt. Ein Quadratmeter dieser Folie kostet $15,30$ Euro. Ermitteln Sie die hierfür anfallenden Materialkosten.
  (4 BE)
  2) Das Objektiv des Beamers, welcher auf die Zeltwand $O A S$ projiziert, befindet sich im Punkt $P (5 | 0 | 4)$ . Laut Herstellerangabe soll zwischen dem Objektiv des Beamers und der Projektionsfläche ein Mindestabstand von $1,8$ Meter eingehalten werden. Überprüfen Sie rechnerisch, ob diese Vorgabe hier erfüllt ist.
  (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung von Punkten, Geraden und Ebenen
  1) Ermitteln Sie die hierfür anfallenden Materialkosten
  Gegeben: Ein Quadratmeter Folie kostet $15,30$ Euro.
  Berechne den Flächeninhalt von drei Pyramidenwänden. (Auf die Zeltwand, an der sich der Zelteingang befindet, wird nicht projiziert.)
  $A = 3 \cdot \frac{1}{2} \cdot | \vec{O A} \times \vec{O S} | = 1,5 \cdot | (\begin{array}{c} 10 \\ 0 \\ 0 \end{array}) \times (\begin{array}{c} 5 \\ 5 \\ 9,3 \end{array}) | = 1,5 \cdot | (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) | = 1,5 \cdot \sqrt{0^{2} + (- 93)^{2} + 50^{2}}$
  $A = 1,5 \cdot \sqrt{11149} \approx 158,38$
  Die drei Pyramidenwandflächen haben einen Flächeninhalt von rund $158,38 m^{2}$ .
  Die Materialkosten betragen $158,38 \cdot 15,30 = 2423,21 €$ .
  2) Überprüfe rechnerisch, ob diese Vorgabe hier erfüllt ist
  Der Punkt $P$ befindet sich vor der Seitenfläche $O A S$ .
  Weiterhin gegeben sind der Punkt $P (5 | 0 | 4)$ , ein Mindestabstand von $1,8$ Meter und die Zeltwand $O A S$ liegt in der Ebene $H : - 93 x_{2} + 50 x_{3} = 0$ .
  $\Rightarrow {\vec{n}}_{H} = (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array})$
  Erstelle die Gleichung einer Lotgeraden $l : \vec{x} = \vec{O P} + r \cdot {\vec{n}}_{H} = (\begin{array}{c} 5 \\ 0 \\ 4 \end{array}) + r \cdot (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array})$ .
  Setze $l$ in $H$ ein, um den Lotfußpunkt $F$ zu erhalten:
  $\Rightarrow - 93 \cdot (- 93 r) + 50 \cdot (4 + 50 r) = 0 \Rightarrow 8649 r + 200 + 2500 r = 0$
  $\Rightarrow 11149 r = - 200 \Rightarrow r = - \frac{200}{11149}$
  $\vec{O F} = (\begin{array}{c} 5 \\ 0 \\ 4 \end{array}) - \frac{200}{11149} \cdot (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array})$
  Der Abstand des Punktes P von der Ebene $E_{O A S}$ ist gleich dem Betrag des Vektors $\vec{P F}$ .
  $| \vec{P F} | = | \vec{O F} - \vec{O P} | = | (\begin{array}{c} 5 \\ 0 \\ 4 \end{array}) - \frac{200}{11149} \cdot (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) - (\begin{array}{c} 5 \\ 0 \\ 4 \end{array}) | = | - \frac{200}{11149} \cdot (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) |$
  $| \vec{P F} | = \frac{200}{11149} \cdot | (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) | = \frac{200}{11149} \cdot \sqrt{11149} \approx 1,89$
  Der Abstand des Punktes $P$ von der Zeltwand beträgt rund $1,89 m$ .
  Der Mindestabstand von $1,8$ Meter ist also erfüllt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Berechne den Flächeninhalt von drei Pyramidenwänden $\Rightarrow A_{1}$ .
  Die Materialkosten betragen $A_{1} \cdot 15,30 €$ .
  Teil 2
  Der Punkt $P$ befindet sich vor der Seitenfläche $O A S$ .
  Erstelle die Gleichung einer Lotgeraden $l$ .
  Setze $l$ in $H$ ein, um den Lotfußpunkt $F$ zu erhalten.
  Der Abstand des Punktes P von der Ebene $E_{O A S}$ ist gleich dem Betrag des Vektors $\vec{P F}$ .
  Überprüfe, ob $| \vec{P F} | > 1,8$ ist.
3. Jeweils zwei benachbarte Zeltwände schließen im Inneren des Zelts einen stumpfen Winkel ein. Ermitteln Sie die Größe dieses Winkels.
  (5 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie
  Ermittle die Größe dieses Winkels
  Nach Aufgabe b) ist ${\vec{n}}_{H} = (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) \Rightarrow | {\vec{n}}_{H} | = \sqrt{11149}$
  Betrachte die Zeltseite $A B S$ .
  Der Normalenvektor der Ebene $E_{A B S}$ ist ${\vec{n}}_{K}$ .
  ${\vec{n}}_{K} = \vec{A S} \times \vec{A B} = (\begin{array}{c} 5 - 10 \\ 5 - 0 \\ 9,3 - 0 \end{array}) \times (\begin{array}{c} 10 - 10 \\ 10 - 0 \\ 0 - 0 \end{array}) = (\begin{array}{c} - 5 \\ 5 \\ 9,3 \end{array}) \times (\begin{array}{c} 0 \\ 10 \\ 0 \end{array}) = (\begin{array}{c} - 93 \\ 0 \\ - 50 \end{array}) \Rightarrow | {\vec{n}}_{K} | = \sqrt{11149}$
  Für den Winkel $φ$ zwischen den beiden Ebenen gilt:
  $\cos φ = \frac{| \vec{n_{H}} \circ \vec{n_{K}} |}{| \vec{n_{H}} | \cdot | \vec{n_{K}} |} = \frac{| (\begin{array}{c} 0 \\ - 93 \\ 50 \end{array}) \circ (\begin{array}{c} - 93 \\ 0 \\ - 50 \end{array}) |}{\sqrt{11149} \cdot \sqrt{11149}} = \frac{2500}{11149}$
  $φ = \cos^{- 1} (\frac{2500}{11149}) \approx {77,04}^{°}$
  Der gesuchte Winkel ist aber laut Aufgabenstellung ein stumpfer Winkel der zwischen $90^{°}$ und $180^{°}$ liegt, d.h. der gesuchte Winkel ist der Nebenwinkel von $φ$ .
  Der Winkel zwischen zwei benachbarten Zeltwänden ist dann $180^{°} - {77,04}^{°} = {102,96}^{°}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Normalenvektor der Ebene $E_{A B S}$ $\Rightarrow {\vec{n}}_{K}$ .
  Für den Winkel $φ$ zwischen den beiden Ebenen gilt: $\cos φ = \frac{| \vec{n_{H}} \circ \vec{n_{K}} |}{| \vec{n_{H}} | \cdot | \vec{n_{K}} |}$
  Der gesuchte Winkel ist aber laut Aufgabenstellung ein stumpfer Winkel, d.h. der gesuchte Winkel ist der Nebenwinkel von $φ$ .
4. Der Zelteingang $D E F G$ hat eine Durchgangshöhe von $2,79 m$ . Der Punkt $G$ liegt auf der Strecke $D S$ und der Punkt $F (8,5 | 6,05 | 2,79)$ auf der Strecke $E S$ . Ermitteln Sie die Koordinaten des Punktes $G$ und zeigen Sie mit Ihrem Ergebnis, dass das Viereck $D E F G$ ein gleichschenkliges Trapez ist.
  [ Teilergebnis: $G (8,5 | 3,95 | 2,79)$ ]
  (6 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
  Ermittle die Koordinaten des Punktes $G$
  Gegeben sind:
  $D (10 | 3,5 | 0)$ , $S (5 | 5 | 9,3)$ und die Durchgangshöhe beträgt $2,79 m$ . Der Punkt $G$ liegt auf der Strecke $D S$ .
  Erstelle die Gleichung der Geraden durch die Punkte $D$ und $S$ .
  Gerade $g_{D S} : \vec{x} = \vec{O D} + r \cdot \vec{D S} = (\begin{array}{c} 10 \\ 3,5 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 5 - 10 \\ 5 - 3,5 \\ 9,3 - 0 \end{array}) = (\begin{array}{c} 10 \\ 3,5 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 5 \\ 1,5 \\ 9,3 \end{array})$
  Der Punkt $G$ liegt in der Ebene $J : x_{3} = 2,79$
  Setze $g_{D S}$ in $J$ ein:
  $0 + 9,3 r = 2,79 \Rightarrow r = \frac{2,79}{9,3} = 0,3$
  Setze $r = 0,3$ in $g_{D S}$ ein:
  $\vec{O G} = (\begin{array}{c} 10 \\ 3,5 \\ 0 \end{array}) + 0,3 \cdot (\begin{array}{c} - 5 \\ 1,5 \\ 9,3 \end{array}) = (\begin{array}{c} 10 + 0,3 \cdot (- 5) \\ 3,5 + 0,3 \cdot 1,5 \\ 0 + 0,3 \cdot 9,3 \end{array}) = (\begin{array}{c} 8,5 \\ 3,95 \\ 2,79 \end{array}) \Rightarrow G (8,5 | 3,95 | 2,79)$
  Zeige mit Deinem Ergebnis, dass das Viereck $D E F G$ ein gleichschenkliges Trapez ist
  Bekannt: $D (10 | 3,5 | 0), E (10 | 6,5 | 0),$ $F (8,5 | 6,05 | 2,79)$ und $G (8,5 | 3,95 | 2,79)$ .
  Dann ist $\vec{G F} = \vec{O F} - \vec{O G} = (\begin{array}{c} 8,5 \\ 6,05 \\ 2,79 \end{array}) - (\begin{array}{c} 8,5 \\ 3,95 \\ 2,79 \end{array}) = (\begin{array}{c} 0 \\ 2,1 \\ 0 \end{array})$ und
  $\vec{D E} = \vec{O E} - \vec{O D} = (\begin{array}{c} 10 \\ 6,5 \\ 0 \end{array}) - (\begin{array}{c} 10 \\ 3,5 \\ 0 \end{array}) = (\begin{array}{c} 0 \\ 3 \\ 0 \end{array})$
  Für ein Trapez muss $\vec{G F} ∥ \vec{D E}$ sein, d.h.
  $\vec{G F} = k \cdot \vec{D E} \Rightarrow (\begin{array}{c} 0 \\ 2,1 \\ 0 \end{array}) = k \cdot (\begin{array}{c} 0 \\ 3 \\ 0 \end{array}) \Rightarrow k = 0,7$ , also parallel.
  Wenn das Viereck $D E F G$ ein gleichschenkliges Trapez sein soll, dann muss $| \vec{D G} | = | \vec{E F} |$ sein.
  $\vec{D G} = \vec{O G} - \vec{O D} = (\begin{array}{c} 8,5 \\ 3,95 \\ 2,79 \end{array}) - (\begin{array}{c} 10 \\ 3,5 \\ 0 \end{array}) = (\begin{array}{c} - 1,5 \\ 0,45 \\ 2,79 \end{array})$ und $| \vec{D G} | = \sqrt{(- 1,5)^{2} + {0,45}^{2} + {2,79}^{2}} = \sqrt{10,2366}$
  $\vec{E F} = \vec{O F} - \vec{O E} = (\begin{array}{c} 8,5 \\ 6,05 \\ 2,79 \end{array}) - (\begin{array}{c} 10 \\ 6,5 \\ 0 \end{array}) = (\begin{array}{c} - 1,5 \\ - 0,45 \\ 2,79 \end{array})$ und $| \vec{E F} | = \sqrt{(- 1,5)^{2} + (- 0,45)^{2} + {2,79}^{2}} = \sqrt{10,2366}$
  $\Rightarrow | \vec{D G} | = | \vec{E F} |$
  Es handelt sich um ein gleichschenkliges Trapez.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Erstelle die Gleichung der Geraden $g_{D S}$ durch die Punkte $D$ und $S$ .
  Der Punkt $G$ liegt in der Ebene $J : x_{3} = 2,79$
  Schneide die Gerade $g_{D S}$ mit J.
  Teil 2
  Für ein Trapez muss $\vec{G F} ∥ \vec{D E}$ sein.
  Wenn das Viereck $D E F G$ ein gleichschenkliges Trapez sein soll, dann muss $| \vec{D G} | = | \vec{E F} |$ sein.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Teil 2 Lineare Algebra und analytische Geometrie II: mit Hilfsmitteln

Ermittle, wie viele Personen sich gleichzeitig im betrachteten Zelt aufhalten dürfen

Hast du eine Frage oder Feedback?

1) Ermitteln Sie die hierfür anfallenden Materialkosten

2) Überprüfe rechnerisch, ob diese Vorgabe hier erfüllt ist

Hast du eine Frage oder Feedback?

Ermittle die Größe dieses Winkels

Hast du eine Frage oder Feedback?

Ermittle die Koordinaten des Punktes G

Zeige mit Deinem Ergebnis, dass das Viereck DEFG ein gleichschenkliges Trapez ist

Hast du eine Frage oder Feedback?

Ermittle die Koordinaten des Punktes $G$

Zeige mit Deinem Ergebnis, dass das Viereck $D E F G$ ein gleichschenkliges Trapez ist