12. Lineare Gleichungssysteme

Wir wollen lineare Gleichungen in mehreren Unbekannten $x_{1}, \dots, x_{n}$ lösen.

Eine (die $i$ -te) Gleichung hat folgendes Aussehen

a_{i, 1} x_{1} + a_{i, 2} x_{2} + \dots + a_{i, n} x_{n} = b_{i}

mit Koeffizienten $a_{i, 1}, a_{i, 2}, \dots, a_{i, n}, b_{i} \in ℝ$ .

Einfaches Beispiel für $n = 2$

2 x_{1} - x_{2} = - 2

Beschreibt eine Gerade in der $(x_{1}, x_{2})$ -Ebene durch die Punkte $(- 1 | 0)$ und $(0 | 2)$ .

Lösbarkeit von LGS

Um eine eindeutige Lösung zu erhalten, muss man auf jeden Fall $n$ Gleichungen für $n$ Unbekannte stellen. (Dadurch ist die eindeutige Lösbarkeit aber leider noch nicht garantiert!)

\begin{array}{rrcc} 2 x_{1} & - x_{2} & = & - 2 \\ x_{1} & + \frac{3}{2} x_{2} & = & 2 \end{array}

Graphisch suchen wir den Schnittpunkt zweier Geraden:

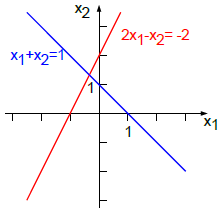
Recht einfach lässt sich das folgende LGS lösen

$\begin{array}{rrcc} 2 x_{1} & - x_{2} & = & - 2 \\ \frac{3}{2} x_{2} & = & 2 \end{array}$

Wir können sofort $x_{2} = \frac{4}{3}$ ablesen und das in die erste Gleichung einsetzen

2 x_{1} - \frac{4}{3} = - 2

was $x_{1} = - \frac{1}{3}$ gibt.

Gauß'sches Eliminationsverfahren

Schön wäre es natürlich, wenn alle unsere LGS in einer solchen Dreiecksform vorliegen würden. Glücklicherweise können wir ein allgemeines LGS leicht in eine solche Form bringen. Diesen Zustand des zweiten Systems können wir aus dem ersten System leicht herstellen, indem wir die erste Gleichung mit $\frac{1}{2}$ multiplizieren und das von der zweiten Gleichung abziehen - wir eliminieren mittels der ersten Gleichung $x_{1}$ aus der zweiten Gleichung.

Wir wollen ein LGS äquivalent umformen (ohne Änderung der Lösungsmenge) durch folgende Strategie:

Mittels der ersten Zeile $x_{1}$ aus Zeilen $2 \dots n$ eliminieren
Mittels der zweiten Zeile $x_{2}$ aus Zeilen $3 \dots n$ eliminieren
…
Mittels der $n - 1$ -ten Zeile $x_{n - 1}$ aus Zeile $n$ eliminieren
Aus dem so entstandenen gestaffelten Dreieckssystem kann man nacheinander $x_{n}$ , $x_{n - 1}$ ,… $x_{2}$ und $x_{1}$ ausrechnen.

Eine Komplikation kann auftreten: wenn im Schritt " $x_{i}$ eliminieren" der (derzeitige) Koeffizient $a_{i, i}$ Null ist, gelingt die Elimination nicht.

In diesem Fall Zeile $i$ mit einer darunter liegenden Zeile vertauschen, bei der in Spalte $i$ keine Null steht (gibt es keine solche Zeile, gibt es keine eindeutige Lösung des LGS).

Um Schreibarbeit zu sparen und zur Implementierung auf dem Computer, lässt man die $x_{i}$ und das $=$ weg. Speichere nur Koeffizienten $a_{i, j}$ und $b_{i}$ .

Beispiel

Bei dem linearen Gleichungssystem

$\begin{array}{rrrcc} x_{1} & - x_{2} & = & 2 \\ - x_{1} & + x_{2} & + x_{3} & = & 1 \\ 2 x_{1} & - x_{3} & = & 3 \end{array}$

sieht der Algorithmus so aus:

$(\begin{array}{ccc} 1 & - 1 & 0 \\ - 1 & 1 & 1 \\ 2 & 0 & - 1 \end{array} | \begin{array}{c} 2 \\ 1 \\ 3 \end{array}) ⇝$ $(\begin{array}{ccc} 1 & - 1 & 0 \\ 0 & 0 & 1 \\ 2 & 0 & - 1 \end{array} | \begin{array}{c} 2 \\ 3 \\ 3 \end{array})$

$⇝ (\begin{array}{ccc} 1 & - 1 & 0 \\ 0 & 0 & 1 \\ 0 & 2 & - 1 \end{array} | \begin{array}{c} 2 \\ 3 \\ - 1 \end{array})$ $⇝ (\begin{array}{ccc} 1 & - 1 & 0 \\ 0 & 2 & - 1 \\ 0 & 0 & 1 \end{array} | \begin{array}{c} 2 \\ - 1 \\ 3 \end{array})$

Wer an dieser Stelle Probleme hat, die Lösung abzulesen, kann sich das einfach wieder als Gleichungssystem hinschreiben:

$\begin{array}{rrrcc} x_{1} & - x_{2} & = & 2 \\ + 2 x_{2} & - x_{3} & = & - 1 \\ + x_{3} & = & 3 \end{array}$

gibt $x_{3} = 3$ , $x_{2} = (- 1 + 3) / 2 = 1$ und $x_{1} = 2 + 1 = 3$ .

Laden

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?