Die orthogonale Affinität beschreibt eine senkrechte Achsenstreckung. Dabei wird ein Punkt auf seinen Bildpunkt abgebildet.
Abbildungsgleichung zur orthogonalen Affinität
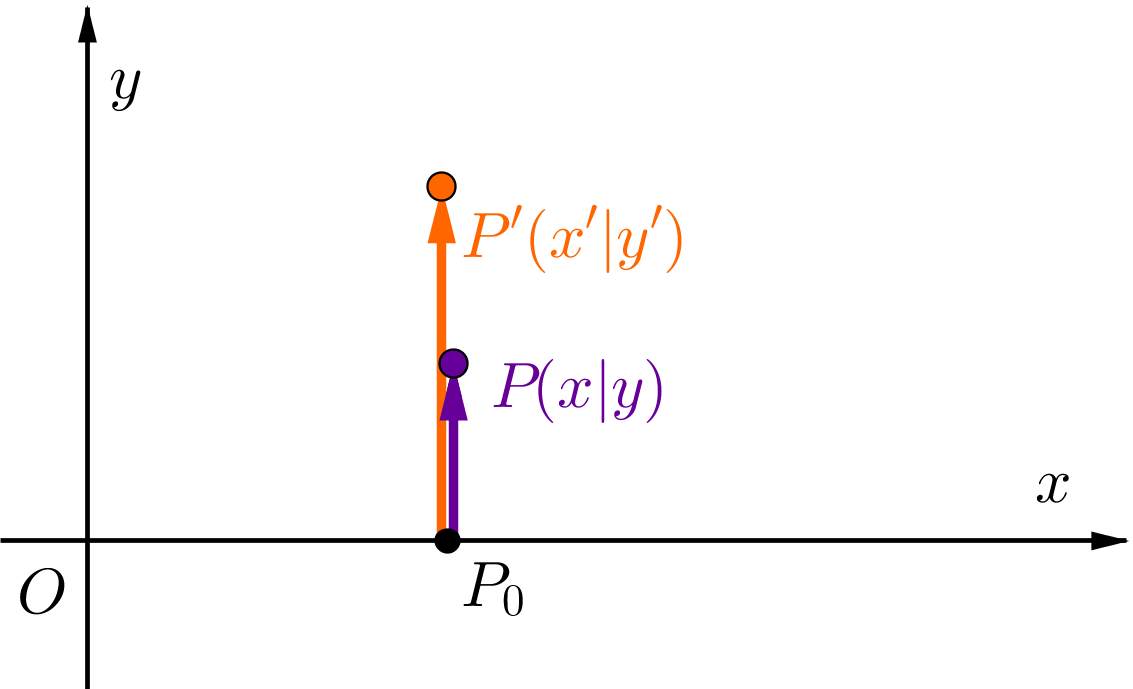
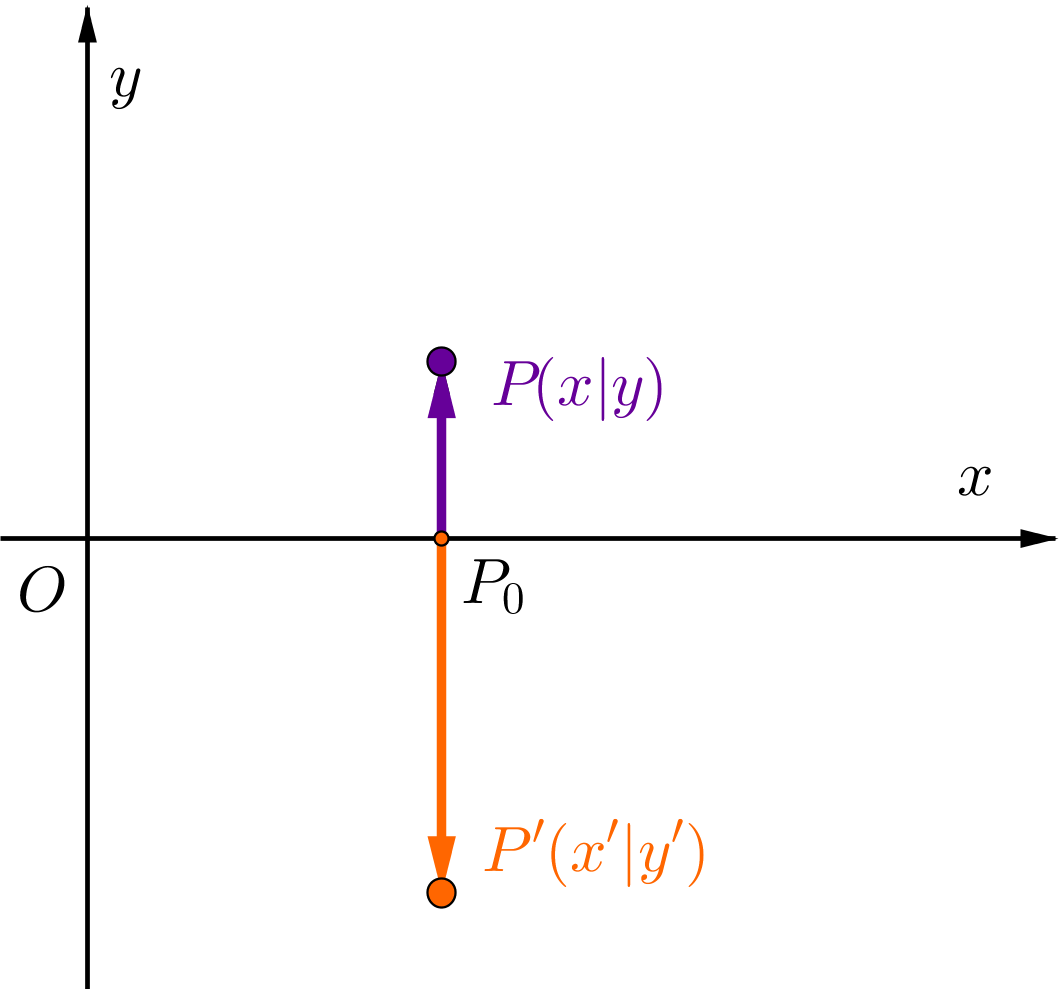
Koordinatenform:
Matrixform:
Beispiel im Applet
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
