6Intervallschachtelung (1/4)
Erklärung | Beispiel |
|---|---|
Betrachte die Wurzel, die du berechnen möchtest. Suche einen bekannten Wurzelwert, der kleiner als die gesuchte Wurzel ist. Suche einen zweiten, der größer als die gesuchte Wurzel ist. | zu berechnen: Du kennst bereits: , Außerdem weißt du: dann gilt, wenn du überall die Wurzel ziehst: |
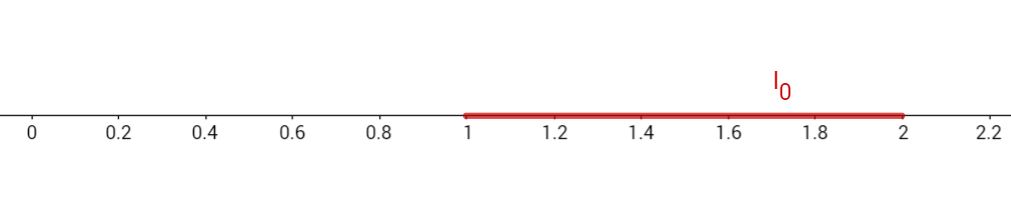
Mit den zwei bekannten Wurzelwerten kannst du nun ein Intervall definieren, in dem der gesuchte Wert liegen muss. | Intervall: |