1 Berechnung von Wurzeln
Inhalt
Der folgende Kurs handelt von Annäherungsverfahren für Wurzelberechnungen.
Am Ende kannst du zwei verschiedene Verfahren anwenden, die du für die Berechnung von Wurzeln nutzen kannst.
Vorwissen
Du solltest wissen:
Was eine Quadratwurzel ist.
Wie man den Mittelwert von zwei Zahlen berechnet.
Wie man den Flächeninhalt von Quadrat und Rechteck berechnet.
Was ein Intervall ist, und seine Bezeichnung.
Dauer
Der Kurs hat eine Dauer von ca. 2h.
2 Motivation
Wie gut kannst du eigentlich Kopfrechnen?
Wenn du gerade die Befürchtung hattest, Kopfrechnen zu müssen: Keine Sorge - es geht um Taschenrechner.
Der praktische Helfer macht den Schulalltag oft sehr angenehm. Doch wie funktioniert er eigentlich?
Bei der Multiplikation ist das ganz klar. Er berechnet das Ergebnis, indem er schriftlich multipliziert.

Auch die Addition von vielen Zahlen ist kein Problem. Per Hand würde man das durch schriftliches Addieren machen.

3 Motivation 2
Doch wie berechnet der Taschenrechner Wurzeln?
Manche Werte, wie , oder sind dir bestimmt schon bekannt. Aber der Taschenrechner liefert uns auch einen Wert für Rechnungen wie , oder .
Wie berechnet er diese?

4 Zwei Vorgehensweisen
Es gibt zwei verschiedene Methoden, mit denen Werte von Wurzeln angenähert werden können.
Das Ergebnis ist dabei oft eine irrationale Zahl, die unendlich viele Stellen hinter dem Komma hat. Diese Zahlen kann auch der Taschenrechner nur annähern und anschließend runden.
Die folgenden zwei Verfahren liefern Näherungswerte und werden auf den nächsten Kursseiten vorgestellt:
5 Intervallschachtelung Einführung
Die Intervallschachtelung ist eine Methode, um die Werte von Wurzeln anzunähern, ohne die Wurzel direkt zu berechnen.
Dabei versuchst du, ein Intervall zu finden, in dem der Wert der Wurzel liegen muss. Dieses Intervall kannst du bis zur gewünschten Genauigkeit schrittweise verkleinern.
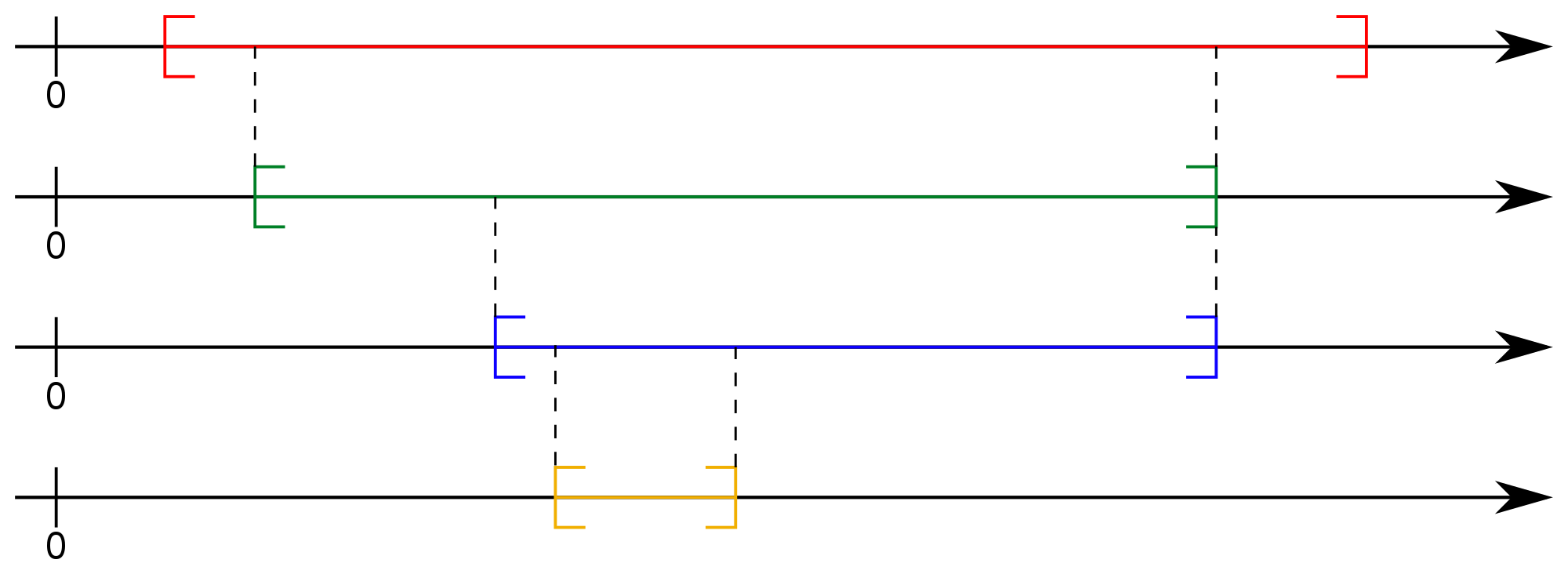
Auf diesem Bild siehst du, wie sich solche Intervalle verkleinern.
6 Intervallschachtelung (1/4)
Erklärung | Beispiel |
|---|---|
Betrachte die Wurzel, die du berechnen möchtest. Suche einen bekannten Wurzelwert, der kleiner als die gesuchte Wurzel ist. Suche einen zweiten, der größer als die gesuchte Wurzel ist. | zu berechnen: Du kennst bereits: , Außerdem weißt du: dann gilt, wenn du überall die Wurzel ziehst: |
Mit den zwei bekannten Wurzelwerten kannst du nun ein Intervall definieren, in dem der gesuchte Wert liegen muss. | Intervall: |
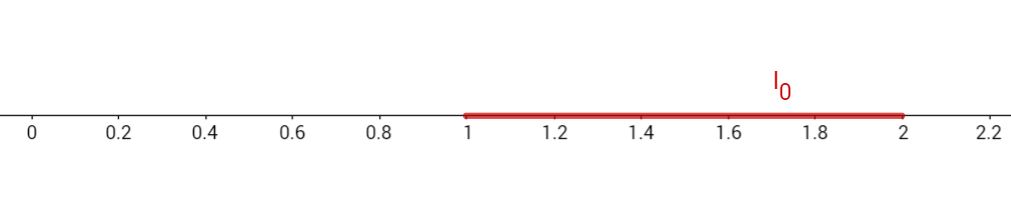
7 Intervallschachtelung (2/4)
Erklärung | Beispiel |
|---|---|
Zunächst suchst du einen neuen Wert, dessen Quadrat in diesem Intervall liegt, aber näher am gesuchten Radikanden ist. | altes Intervall: |
Aus diesem neuen Wert und einem der anderen Werte bildest du ein neues, kleineres Intervall. | |
Den neuen Wert erhältst du, indem du den Mittelwert der alten Werte bildest. Diesen Mittelwert verwendest du später als neue Unter- oder Obergrenze. | Neuer Wert: Mittelwert von und : |
Um dies zu entscheiden, musst du noch testen, ob das Quadrat dieses Wertes größer als der Radikand oder kleiner ist. | Teste, ob größer oder kleiner als ist. |
Wenn er kleiner ist, bildet er zusammen mit der Obergrenze von das neue Intervall . Wenn er größer ist, bildet er zusammen mit der Untergrenze von das neue Intervall . | Neues Intervall: |
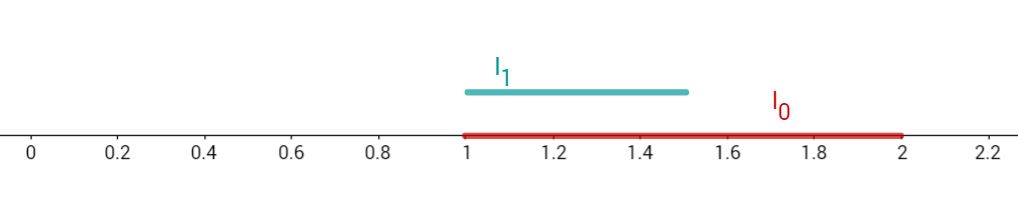
Dieses Verfahren der Verkleinerung von Intervallen wird nun so lange wiederholt, bis du die gewünschte Genauigkeit erreicht hast.
8 Intervallschachtelung (3/4)
In dieser interaktiven Grafik siehst du die Veränderung der Intervallgröße nach jedem Schritt.
Bewege den schwarzen Punkt oben von links nach rechts um einen Schritt weiter zu kommen!
9 Intervallschachtelung (4/4)
Beispiel
Bei würde die Intervallschachtelung folgendermaßen weitergehen:
liegt im Intervall
weil
Intervall | Berechnung |
|---|---|
mit | |
mit | |
mit | |
mit | |
mit |
Diese Tabelle kann man noch beliebig lange fortführen.
Wenn du hier abbrichst, erhältst du als Ergebnis, dass zwischen und liegt.
Oft wird aber noch nach einem Schätzwert gefragt. Jeder Wert aus diesem Intervall wäre ein gültiger Schätzwert. Ein Kandidat wäre hier der Mittelwert.
10 Intervallschachtelung - Aufgabe
Laden
11 Heron-Verfahren Einführung
Eine andere Möglichkeit, das Ergebnis einer Wurzel ungefähr zu bestimmen, liefert das sogenannte Heron-Verfahren.
Grundlage:
Um den Wert der Wurzel zu bestimmen, nutzt du Flächeninhalte. Wir suchen ein Quadrat, dessen Flächeninhalt genau dem Wert des Radikanden entspricht. Die Seitenlänge entspricht dabei genau dem Wert der Wurzel. Dieser Zusammenhang ergibt sich aus dem Flächeninhalt eines Quadrats:
Zum Beispiel zur Berechnung der :
Um dieses Quadrat anzunähern, verwendest du ein Rechteck, dessen Flächeninhalt gleich dem Radikanden ist.Der Flächeninhalt des Rechtecks ergibt sich aus
Um vom Rechteck auf ein Quadrat zu kommen, musst du die längere Seite verkürzen und die kürzere Seite verlängern. Wie genau du dabei vorgehst, lernst du auf den nächsten Seiten.
Dieses Vorgehen kannst du nach Belieben wiederholen, um immer näher an eine quadratische Form zu kommen.
Je geringer die Differenz zwischen und , desto genauer ist das Ergebnis, weil sich das Rechteck einem Quadrat annähert.
12 Heron-Verfahren (1/3)
Vorgehen anhand des Beispiels :
Vorgehen | Beispiel |
|---|---|
Wähle ein Rechteck, das den Flächeninhalt des Radikanden besitzt. Dazu suchst du einen Teiler des Radikanden, den du als erste Seite des Rechtecks nutzt. Die zweite Seite erhältst du durch: | Suche ein Rechteck mit Flächeninhalt . Du kannst z. B. die Seitenlängen und wählen. Ziel: Mache dieses Rechteck möglichst quadratisch. Das geht mit folgender Herangehensweise. |

13 Heron-Verfahren (2/3)
Vorgehen | Beispiel |
|---|---|
Die längere Seite veränderst du wie folgt: | |
Die kürzere Seite veränderst du wie folgt: | |
Damit ist gesichert, dass der Flächeninhalt gleich dem Radikanden ist.
Nun hast du nach diesem Schritt ein Rechteck mit Seitenlängen und .
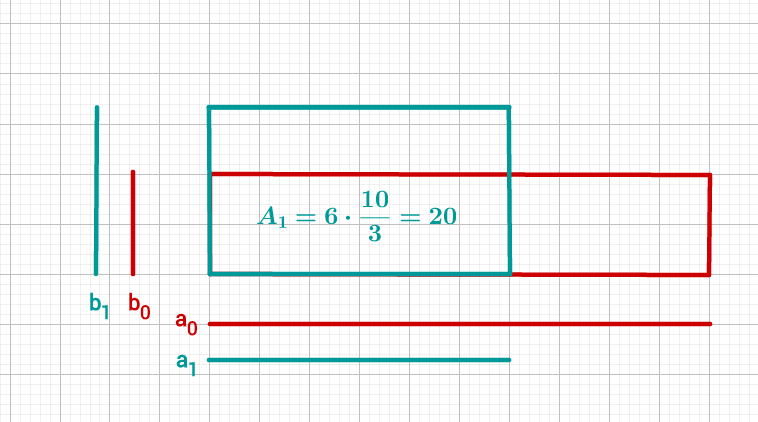
14 Heron-Verfahren (3/3)
Vorgehen | Beispiel |
|---|---|
Die längere Seite veränderst du wie folgt. | |
Die kürzere Seite veränderst du wie folgt. | |
Wiederhole die letzten beiden Schritte.
Nun hast du ein Rechteck mit den Seitenlängen und .

Du kannst sehen, dass sich die beiden Werte annähern.
Das exakte Ergebnis liegt zwischen diesen beiden Zahlen. Wiederholst du dieses Verfahren, so erhältst du .
Zum Vergleich: Der Taschenrechner liefert den gerundeten Wert .
15 Veranschaulichung des Heron-Verfahrens
Im folgenden Applet kannst du eine beliebige Wurzel von 1 bis 50 eingeben und für diese das Heron-Verfahren ansehen.
Den nächsten Schritt des Heron-Verfahrens kannst du ansehen, indem du „nächster Schritt” anklickst.
Die Wurzel, die du berechnen möchtest, änderst du durch Auswählen des Feldes unter der Wurzel. Hier kannst du Zahlen mit einer Nachkommastelle im Bereich zwischen und eingeben.
16 Heron-Verfahren Aufgaben
Aufgabe 1
Laden
Aufgabe 2
Vergleiche die Aufgabe zur Intervallschachtelung und die zum Heron-Verfahren.
Welche Methode der Abschätzung findest du besser und warum?
17 Vergleich Intervallschachtelung - Heron-Verfahren
In den Aufgaben hast du zwei verschiedene Verfahren angewendet und dabei unterschiedliche Werte für erhalten:
Wie kannst du jetzt entscheiden, welches Ergebnis genauer ist?
Du weißt: Quadriere die beiden berechneten Werte und vergleiche, welcher näher an ist.
Intervallschachtelung:
Heron-Verfahren:
Wie du siehst, ist der Wert des Heron-Verfahrens näher an . Auch der Taschenrechner gibt einen Wert von aus.
Außerdem hast du für das Heron-Verfahren weniger Schritte gebraucht als für die Intervallschachtelung.
Die meisten Taschenrechner nutzen das Heronverfahren, um Wurzeln anzunähern. Dieses erreicht mit gleich vielen Schritten eine höhere Genauigkeit. Den Näherungswert rundet er anschließend und zeigt eine bestimmte Anzahl an Dezimalstellen an.
