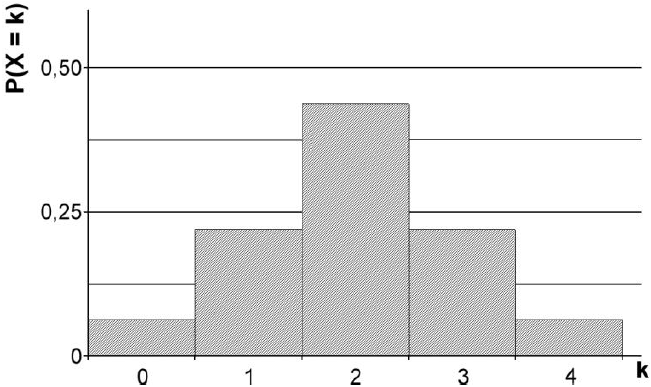
In der Abbildung ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße mit der Wertemenge und dem Erwartungswert dargestellt. Weisen Sie nach, dass es sich dabei nicht um eine Binomialverteilung handeln kann. (3 BE)

In der Abbildung ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße mit der Wertemenge und dem Erwartungswert dargestellt. Weisen Sie nach, dass es sich dabei nicht um eine Binomialverteilung handeln kann. (3 BE)