Es kann vorkommen, dass eine Fläche unter einem Funktionsgraphen betrachtet wird, die in einer Richtung unbeschränkt ist. Dies ist dann der Fall, wenn die Funktion an mindestens einer Integralgrenze nicht definiert ist. Solche Integrale nennt man uneigentliche Integrale und berechnet man über eine Grenzwertbetrachtung an der betroffenen Grenze.
Beispiele
Beispiele sind:
oder
Video zum uneigentlichen Integral
Laden
Beispiel eines uneigentlichen Integrals
Gesucht ist die Fläche, die der Graph der Funktion mit den beiden Koordinatenachsen aufspannt.
Wenn man versucht diese Fläche auf herkömmlichem Weg zu berechnen, stößt man auf das Problem, dass der Graph gar keine Nullstelle hat, er schneidet die x-Achse nicht.
Man lässt zur Berechnung eine feste Grenze gegen unendlich laufen.
Die Fläche ist also genau .
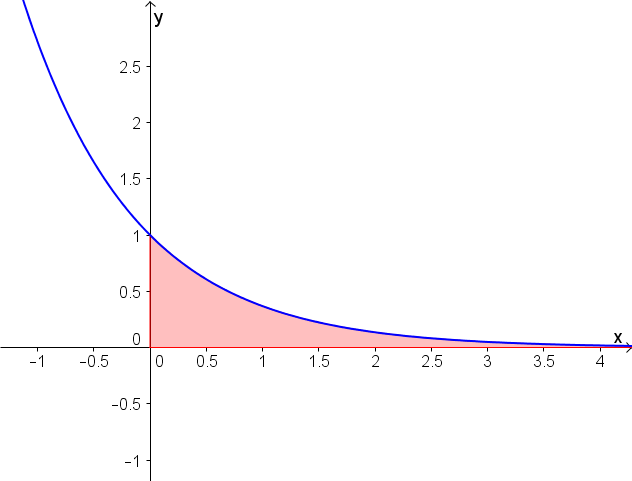
Im Allgemeinen muss ein uneigentliches Integral keine Lösung besitzen. Eine Lösung existiert nur, wenn die Stammfunktion gegen den betrachteten Wert einen endlichen Grenzwert besitzt, wie hier die . Ansonsten gibt es keine Lösung, oder man sagt, die Fläche besitzt keinen endlichen Flächeninhalt (nicht "Die Fläche besitzt unendlichen Flächeninhalt"!).
Analog zu oben, kann man das uneigentliche Integral auch für negative Grenzen bestimmen, oder Grenzen, bei denen der y-Wert gegen unendlich läuft.
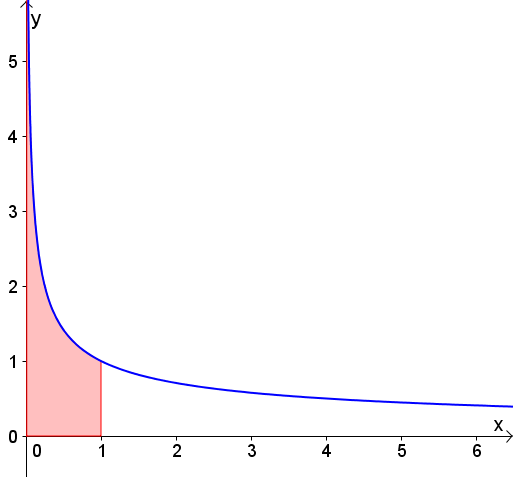
Ein Beispiel wäre die Funktion im Intervall bis .
Bei 0 würde der -Wert unendlich.
Mit einem uneigentlichen Integral lässt sich die Fläche berechnen:
Ein anderes Resultat ergibt sich jedoch für . In diesem Fall müssen beide Integralgrenzen separat als Limes betrachtet werden.
Das Integral
In diesem Abschnitt wird das unbestimmte Integral in Abhängigkeit einer rationalen Zahl betrachtet:
1. Fall: :
Dabei benutzt man, dass negativ ist.
2. Fall: :
Man verwendet: .
3. Fall: :
Dies ergibt sich, da für positiv ist.
Bemerkung: Eine ähnliche Betrachtung ist für möglich.
