2I. Ebenen als Lösungen von linearen Gleichungen mit drei Unbekannten
Eine lineare Gleichung mit drei Unbekannten - die Koordinatenform einer Ebene
Eine Alternative zu der Paramterform ist die Koordinatenform. Die Koordinatenform bietet eine Variante zur Darstellung einer Ebene, die im ersten Zugang nicht so anschaulich wirkt. Sie bietet dafür aber insgesamt sehr viele Rechenvorteile.
Im folgenden wird zuerst ein Beispiel für eine Ebenengleichung in Koordinatenform dargestellt. Hier wird der Fokus zuerst nur auf die algebraische Perspektive gelegt. Erst später wird dann im nächsten Unterkapitel die allgemeine Ebenengleichung hergeleitet und vollständig erklärt.
Ein Beispiel für eine Ebenengleichung ist:
Beispiel:
oder auch:
Hier stehen die drei Buchstaben , und (bzw. und ) für die drei Koordinaten eines Vektors. Wofür die drei Koeffizienten stehen, wird später im nächsten Teilkapitel erklärt. Auch warum diese Gleichung gerade eine Ebene im drei dimensionalen Raum beschreibt, wird erst im nächsten Teilkapitel erklärt. Hier soll die Ebenengleichung in einem ersten Schritt als eine lineare Gleichung mit drei Variablen betrachtet werden.
Lineare Gleichungen mit zwei Variablen kennst du bereits aus der Mittelstufe. Dort taucht schon eine ganz ähnliche Gleichung wie die obige auf, die dir vertraut sein sollte. Denn eine Gerade kann beschrieben werden durch:
Nur durch einfache Äquivalenzumformungen erhälst du hieraus folgende Darstellung:
Ersetzt du nun noch die Bezeichnungen durch und durch , so sieht die dir bekannte Geradengleichung der dir noch unbekannten Ebenengleichung schon sehr ähnlich:
Der einzige Unterschied besteht nun noch darin, dass in der Ebenengleichung noch ein weiterer Summand auftritt. Ihn brauchst du, um vom zwei-Dimensionalen ins drei-Dimensionale zu gelangen.
Sowohl eine lineare Gleichung mit zwei Variablen wie als auch eine lineare Gleichung mit drei Variablen wie haben unendlich viele Lösungen. Alle Lösungen von lassen sich als Punkte im zwei-dimensionalen Koordinatensystem visualisieren. Ebenso lassen sich alle Lösungen von als Punkte im dreidimensionalen Raum visualisieren. Beide Gleichungen beschreiben deshalb einmal eine Gerade und einmal eine Ebene, weil alle Lösungen der jeweiligen Gleichung einmal auf einer Geraden und beim anderen Mal auf einer Ebene liegen. Bevor erklärt wird, warum die Lösungen der Gleichung alle in einer Ebene liegen, sollst du noch lernen, wie solche Lösungen bestimmt werden können und wie überprüft werden kann, ob ein Zahlentriple eine Lösung ist oder nicht.
Bestimme mindestens drei Lösungen von
Auf genau die gleiche Weise kannst du auch Lösungen von bestimmen: Für zwei Variablen kannst du willkürliche Zahlen festlegen und die Zahl für die dritte Variable kannst du dann einfach durch das Lösen der linearen Gleichung bestimmen.
Bestimme in so, dass P eine Lösung von ist.
Gucke dir nun die beiden Punkte und mit und an. Wenn du die Koordinaten der beiden Punkte jeweils für die Variablen in der Ebenengleichung einsetzt, kanst du überprüfen, ob die Punkte in der Ebene liegen. Die Punkte liegen in der Ebene genau dann, wenn sie eine Lösung der Ebenengleichung sind. Dieses Verfahren nennt man, genauso wie auch bei Geraden, Punktprobe.
Probier es einmal aus!
Liegen und in ?
Im ersten Fall kommt eine unwahre Aussage heraus (), der Punkt P liegt also nicht in der Ebene. Im zweiten Fall kommt dagegen eine wahre Aussage heraus (), also liegt der Punkt in der Ebene.
Fazit:
Insgeamt ist es so, dass alle Punkte, die diese Gleichung der Ebene erfüllen, tatsächlich in der Ebene liegen. Die Ebene ensteht also durch unendliche viele Punkte, deren Koordinaten alle die Koordinatengleichung erfüllen.
Dieser Zusammenhang wird im folgenden Bild dargestellt: Du siehst drei rote Punkte. Diese Punkte sind die Schnittpunkte der Ebene mit den Koordinatenachsen. Sie heißen Spurpunkte. Ihre Koordinaten sind: , und . Wie man sie berechnet, erfährst du im nächsten Absatz. Weiterhin siehst du sehr viele blaue Punkte. Jeder Punkt mit seinen drei Koordinaten ist eine Lösung der Ebenengleichung. Die Ebene ensteht also durch unendlich viele von diesen Punkten. Im Bild sind freilich 'nur' ca. 200 solcher Punkte eingezeichnet:
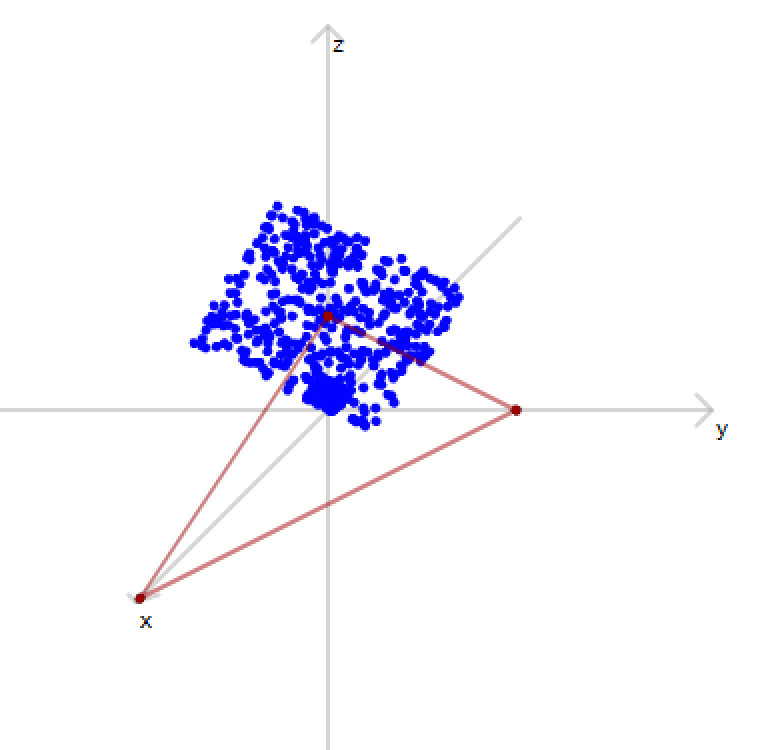
Du kannst dir also eine Ebene in der Koordinatenform gut vorstellen, als eine ebene Punktwolke, deren Punkte so dicht liegen, dass zwischen ihnen kein Platz mehr ist.
