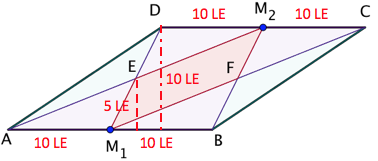
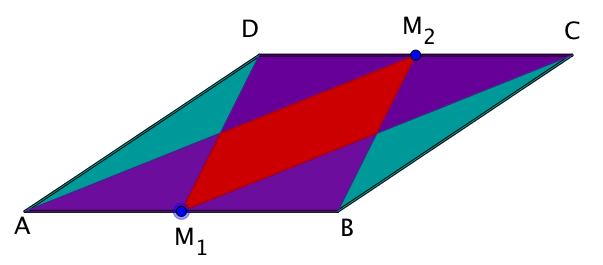
Parkettierung eines Parallelogramms
Unter einer Parkettierung einer geometrischen Figur versteht man die vollständige überschneidungsfreie Überdeckung der Figur mit Teilfiguren.
Für das gezeichnete Parallelogramm gelte , die zugehörige Höhe betrage . und seien Mittelpunkte der Parallelogrammseiten.
Berechne die Flächeninhalte der überdeckenden Teilfiguren.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?