Berechne die (rot markierten) gesuchten Größen. Runde das Ergebnis auf zwei Nachkommastellen.
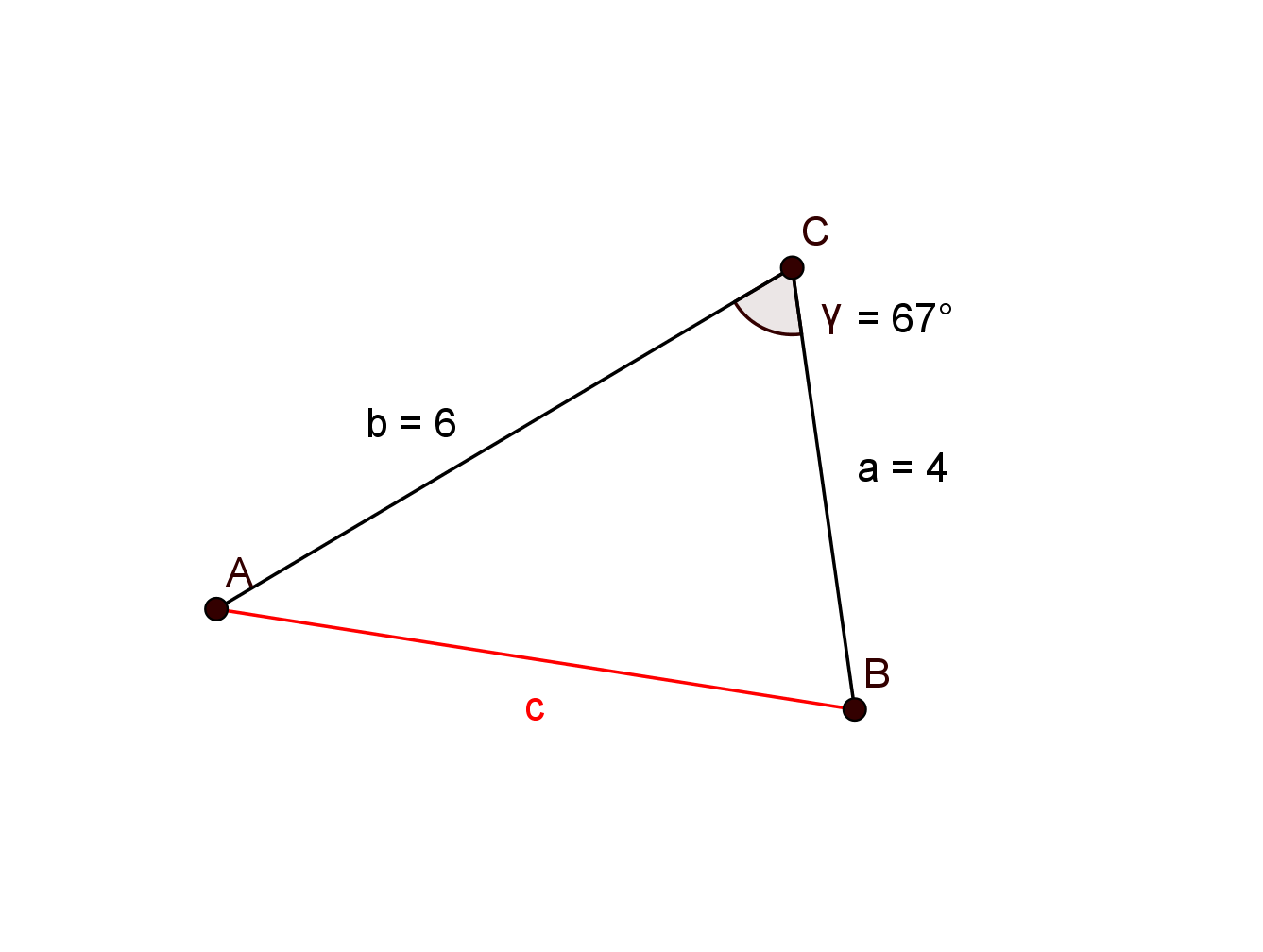
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kosinussatz
Gegeben:
Gesucht:
Der gegebene Winkel ist von den beiden gegebenen Seiten eingeschlossen. Verwende deshalb den Kosinussatz.
↓ Setze die gegebenen Werte ein.
↓ Rechne die rechte Seite zusammen.
↓ Ziehe die Wurzel. Runde auf 2 Nachkommastellen.
Hast du eine Frage oder Feedback?
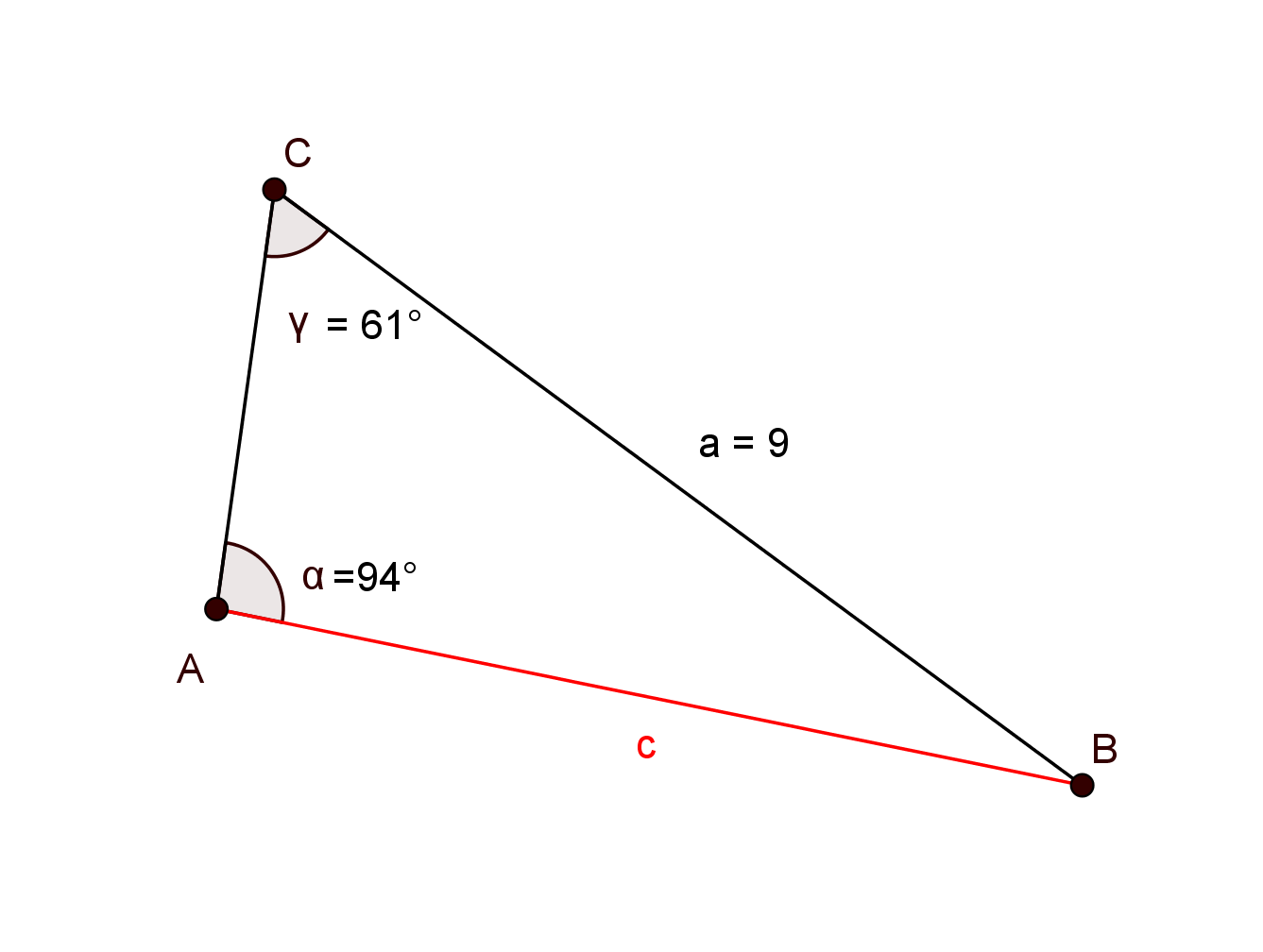
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz
Gegeben:
Gesucht:
Du hast zwei Winkel und eine (einem der Winkel gegenüberliegende) Seite gegeben. Verwende deshalb den Sinussatz. Schreibe die Unbekannte c links oben in die Gleichung.
↓ Forme nach der gesuchten Größe um. Multipliziere hierzu mit .
↓ Setze die Werte ein.
Hast du eine Frage oder Feedback?
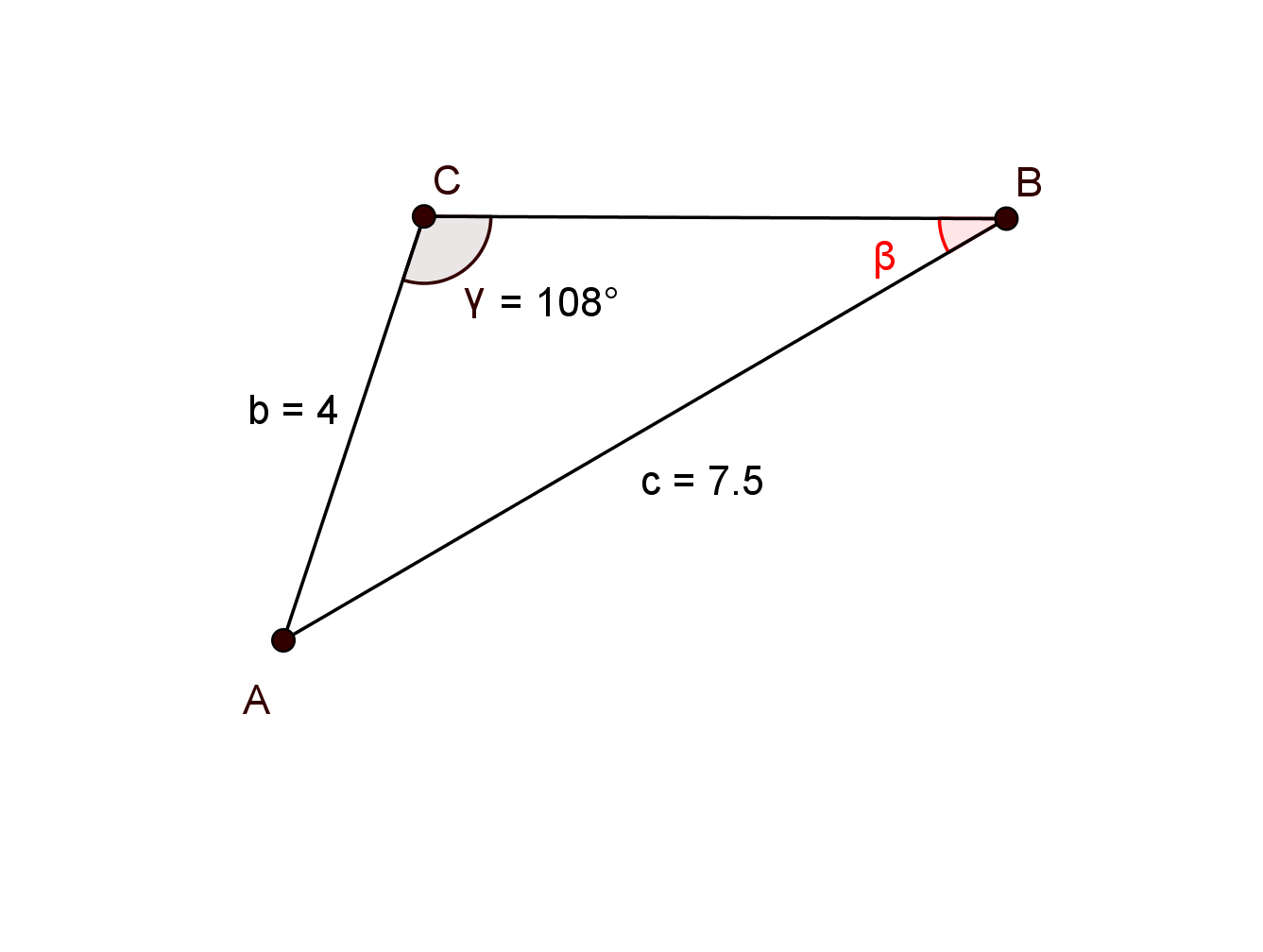 °
°Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz
Gegeben:
Gesucht:
Du hast ein Paar aus Winkel und gegenüberliegender Seite und die Seite gegenüber dem gesuchten Winkel gegeben. Verwende deshalb den Sinussatz.
↓ Tipp: Indem du von beiden Brüchen den Kehrbruch bildest, kannst du die gesuchte Größe in den Zähler bekommen.
↓ Löse nach der gesuchten Größe auf.
↓ Setze die gegebenen Werte ein.
↓ Rechne aus.
↓ Löse nach dem Winkel auf.
Hast du eine Frage oder Feedback?
 °
°Für diese Aufgabe benötigst Du folgendes Grundwissen: Kosinussatz
Gegeben:
Gesucht:
Du hast drei Seiten gegeben und suchst einen Winkel. Verwende deshalb den Kosinussatz. Da der gesuchte Winkel der Winkel ist, ist die gegenüberliegende Seite, die beim Kosinussatz allein steht.
↓ Forme nach um.
↓ Setze die gegebenen Werte ein.
↓ Rechne aus und runde auf 2 Nachkommastellen.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
