Der Begriff der Menge ist eines der wichtigsten und grundlegendsten Konzepte der Mathematik. Das ist auch der Grund, warum er dir schon so früh im Studium begegnet. Doch was ist eine Menge?
Hierzu möchten wir die originale Definition von Georg Cantor, dem Begründer der Mengenlehre, aus dem Jahr 1895 verwenden:
Cantors originale Mengendefinition
„Unter einer ‚Menge‘ verstehen wir jede Zusammenfassung von bestimmten wohlunterschiedenen Obje[k]ten uns[e]rer Anschauung oder unseres Denkens (welche die ‚Elemente‘ von genannt werden) zu einem Ganzen.“[1]
Eine Menge ist also der Zusammenschluss von verschiedenen Objekten zu einem neuen Objekt, welches all die zusammengeschlossenen Objekte umfasst. Betrachte hierzu folgende Polygone:
Diese Polygone wurden zu einer Menge zusammengeschlossen, was durch die Ellipse angedeutet wird. Hier könnte man sich die Menge als eine Art „Behältnis“ vorstellen, welche alle Polygone als Inhalt enthält. Dieses Bild ist jedoch nicht ganz korrekt. Ein Behältnis bleibt nämlich dasselbe, auch wenn man seinen Inhalt ändert. Dies ist bei Mengen anders: Diese ändern ihre Identität, wenn man neue Elemente hinzufügt oder bestehende entfernt.
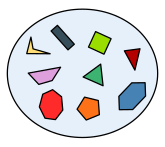 |  |  |
|---|---|---|
Eine Beispielmenge | Dieselbe Menge als imaginäre Box | Bessere Vorstellung: Menge als Inhalt einer imaginären Box |
Diese Vorstellung entspricht in etwa dem alltäglichen Gebrauch des Begriffs „Menge“. Nimm den alltäglichen Begriff einer „Menschenmenge in einem Stadion“ als anschauliches Beispiel: Eine Menschenmenge in einem Stadion.
Niemand würde diese Menge mit dem Stadion, was in unserem Beispiel quasi das Behältnis ist, gleichsetzen. Vielmehr entspricht die (Menschen-)Menge im Stadion der Zusammenfassung von allen Personen innerhalb des Stadions zu einem Ganzen. Diese Menge kann man dabei als „Inhalt des Stadions“ auffassen, wobei wir für dieses Beispiel alle anderen Gegenstände innerhalb des Stadions nicht beachten. Wenn neue Personen das Stadion betreten oder verlassen, dann ändert sich auch die Menge der Leute im Stadion. Genauso verändern Mengen in der Mathematik ihre Identität, wenn Elemente entfernt oder hinzugefügt werden.
Beachte, dass wir in diesem Beispiel mit der Menschenmenge im Stadion was anderes als die Anzahl der Leute im Stadion meinen. Unsere Menge ändert sich, wenn beispielsweise eine Person das Stadion verlässt und danach eine andere Person das Stadion betritt. Genauso ist es auch in der Mathematik: Wenn du innerhalb einer Menge ein Objekt mit einem anderen austauscht, dann veränderst du die Identität dieser Menge. Ignoriere bitte auch Unzulänglichkeiten, die in diesem anschaulichen Beispiel aus mathematischer Sicht stecken. Beispielsweise haben wir nicht geklärt, was ein Mensch ist und was seine Identität ausmacht...
Anders als in der realen Welt, wo Behältnisse und damit ihre Inhalte räumlich begrenzt sind, können Mengen beliebig groß sein und unendlich viele Elemente umfassen. Auch müssen ihre Elemente keine gemeinsamen Eigenschaften besitzen. Sie können sehr unterschiedlich sein.

Grundlegende Notationen für Mengen
Zur Bezeichnung von Mengen werden in der Regel Großbuchstaben verwendet. Wenn die Elemente einer Menge selbst keine Mengen sind, nutzt man für sie oft Kleinbuchstaben. Man schreibt – „ ist ein Element von “, wenn eines der Objekte bezeichnet, das in der Menge enthalten ist. Ist dies nicht der Fall, schreibt man – „ ist kein Element von “.
Das Element-Symbol wurde im Übrigen 1889 von Giuseppe Peano in seiner Arbeit Arithmetices principia nova methodo exposita eingeführt. Es ist eine veränderte Darstellung des Anfangsbuchstaben ε (Epsilon) vom griechischen Wort εστί („estí“, was „ist“ bedeutet)[2].

Beispiele für Mengen
Stelle dir folgende Ansammlung von Objekten vor:
Aus dieser Ansammlung können wir die vier Objekte Trommel, Spielkarte, Digitalkamera und Gitarre zu einer Menge zusammenfassen:
Wenn wir die gerade von uns gebildete Menge mit bezeichnen, so können wir aufschreiben:
„Die Trommel ist ein Element der Menge .“ | |
„Das Buch ist kein Element der Menge . |
Laden
Zahlenbereiche als Mengen
Auch Zahlenbereiche werden in der Mathematik als Mengen aufgefasst. So ist die Menge der natürlichen Zahlen die Zusammenfassung aller Zahlen zu einer Menge. Diese Menge wird mit dem Buchstaben mit (meistens links) doppelter Vertikalen notiert. Auch andere Zahlenbereiche werden als Mengen aufgefasst:
Zahlenbereich | Symbol |
|---|---|
Natürliche Zahlen |
|
Ganze Zahlen | |
Rationale Zahlen | |
Reelle Zahlen | |
Komplexe Zahlen |
Laden
Die Extensionalität von Mengen
Die Identität einer Menge manifestiert sich allein dadurch, welche Objekte sie enthält. Zwei Mengen sind nämlich genau dann gleich, wenn sie dieselben Elemente besitzen. Diese beiden Mengen sind dann ein- und dasselbe Objekt. So gibt es beispielsweise nur eine Menge, welche genau die Zahlen und enthält.
Mehrere Mengen mit denselben Elementen kann es nicht geben.
Wenn es auch nur ein Objekt gibt, welches Element der einen Menge, aber nicht der anderen ist, dann sind beide Mengen verschieden. Diese Eigenschaft von Mengen wird Extensionalitätsprinzip oder auch Extensionalitätsaxiom genannt. Sie lässt sich wie folgt formalisieren:
Für zwei beliebige Mengen und gilt:
Übersetzt bedeutet obige Formel:
Würden wir Mengen, die über unterschiedliche Eigenschaften definiert sind, als unterschiedlich betrachten (eine solche Mengenlehre wäre intensional), wäre sie für die Mathematik nicht brauchbar. Wie aber aus dem obigen Extensionalitätsprinzip hervorgeht, ist es für die Identität einer Menge egal, wie sie gebildet wurde. Es ist nur wichtig zu wissen, welche Elemente sie umfasst.
In unserer Mengenlehre ist die Menge aller Lösungen der Gleichung identisch mit der Menge aller Lösungen der Gleichung . Dies ist die Menge bestehend aus den Zahlen und . In einer intensionalen Mengenlehre wäre dies nicht zwangsläufig der Fall, da beide Mengen durch unterschiedliche Eigenschaften definiert sind.
Wozu braucht man Mengen in der Mathematik?
Mengen werden dir in allen Teilgebieten der Mathematik begegnen. Sie sind ein praktisches Hilfsmittel und mit ihnen können komplexe Sachverhalte kurz und prägnant ausgedrückt werden. Auch können mit Mengen neue Objekte konstruiert oder Konzepte modelliert werden. Beispielsweise nutzt die Topologie Mengen, um Nachbarschaftsbeziehungen auszudrücken und auch die in der Algebra studierten Strukturen wie Gruppen oder Körper werden als Mengen definiert.
Daneben ist die Mengenlehre selbst ein etabliertes Teilgebiet der Mathematik. Hier haben Mathematiker gezeigt, dass alle wesentlichen Konzepte der Mathematik allein mit Mengen modelliert werden können. Trotz des simplen Charakters ist der Mengenbegriff also sehr mächtig. So kann beispielsweise jede Zahl als ein komplexes Mengengebilde dargestellt werden[3]. Über die Mengenlehre können so Grundfragen der Mathematik beantwortet werden (eben weil man sich auf den Standpunkt stellen kann, alles in der Mathematik sei Menge)[4]. Beispielsweise besitzt die Mengenlehre Mittel, um für eine Aussage zu beweisen, dass sie innerhalb eines gegebenen Axiomensystems weder beweisbar noch widerlegbar ist[5].
Wenn man sich die Einfachheit und die Bedeutung der Mengenlehre vor Augen hält, dann wundert es schon ein wenig, dass die Mengenlehre eine für die Mathematik recht junge Theorie ist.
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Mengenlehre
