Das Zählprinzip hilft, die Anzahl der Möglichkeiten zu bestimmen, die es in einem Zufallsexperiment gibt.
Bei einem mehrstufigen Zufallsexperiment, gibt es in jeder Stufe eine bestimmte Anzahl von Möglichkeiten. Diese Anzahlen von Möglichkeiten werden miteinander multipliziert.
Bei einem Bücherregal gibt es noch freie Plätze. Darin möchte man Bücher hineinstellen, stellt jedoch fest, dass es verschiedene Möglichkeiten dafür gibt.
Das Zählprinzip:
3 Möglichkeiten für das erste Buch.
2 Möglichkeiten für das zweite.
1 Möglichkeit für das dritte.
Die Gesamtzahl der Möglichkeiten ist:

Beispiele zu mehrstufigen Möglichkeiten
Essen im Restaurant
In einem beliebten Restaurant kann man sein Menü selbst zusammenstellen. Man hat die Wahl aus 2 Vorspeisen (Suppe, Salat), 3 Hauptspeisen (Pasta, Schnitzel, Fisch) und 2 Nachspeisen (Eis, Tiramisu). Auf wie viele verschiedene Arten kann man sein Menü zusammenstellen?

Diese Aufgabe kann man lösen, indem man alle Möglichkeiten in einem Baumdiagramm darstellt.
Nun kann die Anzahl der Möglichkeiten am Baumdiagramm abgezählt werden. Es gibt insgesamt 12 Möglichkeiten, sein Menü zusammenzustellen.
Einfacher, als ein Baumdiagramm zeichnen zu müssen, ist der Weg über das Zählprinzip. Es werden drei Entscheidungen getroffen. Es gibt 2 Möglichkeiten für die Vorspeise, 3 Möglichkeiten für das Hauptgericht und zwei Möglichkeiten für den Nachtisch. Nach dem allgemeinen Zählprinzip der Kombinatorik ist die Anzahl der Möglichkeiten das Produkt der Möglichkeiten der einzelnen Entscheidungen.
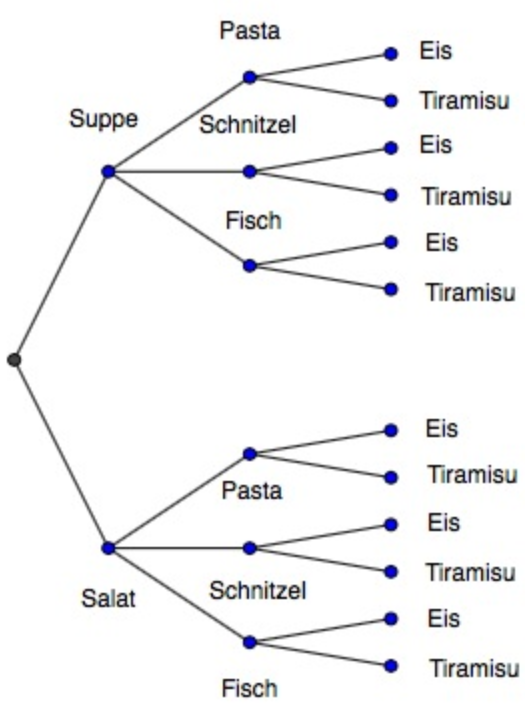
Insgesamt gibt es also Möglichkeiten.
Sitzordnungen
Wie viele Sitzordnungen sind bei einer Gruppe von 4 Schülern möglich?
Der erste Schüler hat vier verschiedene Möglichkeiten, sich hinzusetzen, da noch kein Stuhl besetzt ist.

Nachdem sich der erste Schüler hingesetzt hat, sind von den vier Stühlen nur noch drei frei. Daher gibt es für den zweiten Schüler nur noch drei Möglichkeiten, auf welchen Stuhl er sich setzen möchte.

Für den dritten Schüler gibt es dann nur noch 2 Möglichkeiten, auf welchen der beiden verbliebenen Stühle er sich setzen möchte. Der vierte Schüler muss sich auf den letzten verbliebenen Stuhl setzen, hat also genau 1 Möglichkeit.
Nach dem Zählprinzip ist die Anzahl der Möglichkeiten, eine Sitzordnung mit 4 Schülern aufzustellen, das Produkt aus den Möglichkeiten für die einzelnen Schüler.
Somit gibt es verschiedene Sitzordnungen.
Hierfür kann man auch mit der Schreibweise für die Fakultät schreiben.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
