Aufgaben zu zusammengesetzten Zufallsexperimenten
Wie gut kennst du dich aus? Lerne, mit diesen Aufgaben Wahrscheinlichkeiten von zusammengesetzten Zufallsexperimenten zu berechnen.
- 1
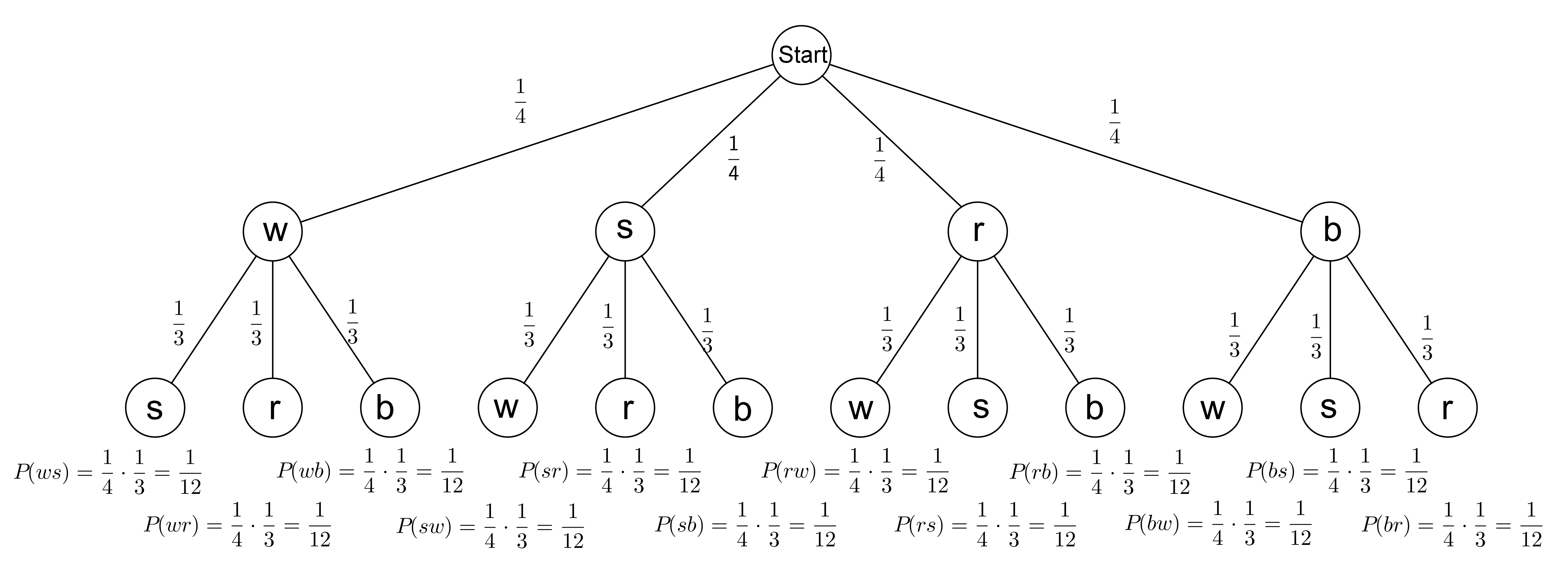
In einer Urne befinden sich eine weiße, eine schwarze, eine rote und eine blaue Kugel. Es werden nacheinander (und ohne Zurücklegen) zwei Kugeln entnommen.
Zeichne ein Baumdiagramm und lies den Ergebnisraum dieses Zufallsexperiments ab.
Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
A: Keine der gezogenen Kugeln ist rot.
B: Unter den gezogenen Kugeln ist eine rote.
C: Es werden zwei rote Kugeln gezogen.
D: Die gezogenen Kugeln sind weiß und schwarz.
Gib in Worten ein Ereignis E mit der Wahrscheinlichkeit und ein Ereignis F mit der Wahrscheinlichkeit an.
- 2
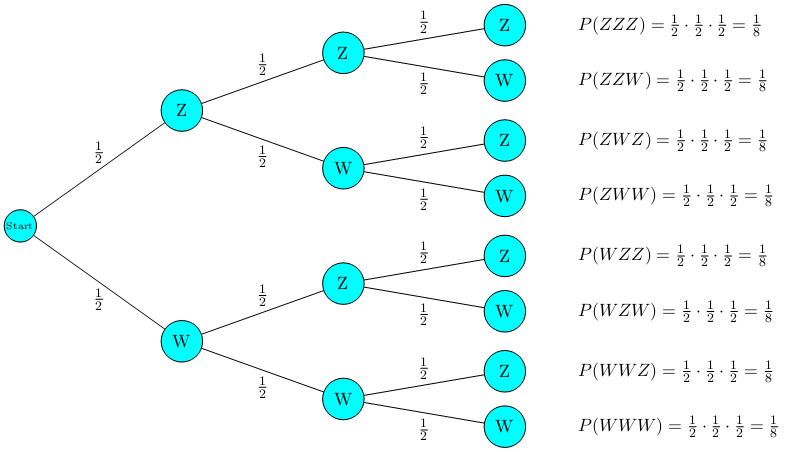
Zeichne den Baum für den dreifachen Münzenwurf Wappen(W) und Zahl(Z) und bestimme die Wahrscheinlichkeiten der einzelnen Ergebnisse.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?