Zunächst werden wir in einem einführenden Beispiel die vorkommenden Begriffe motivieren. Im zweiten Abschnitt werden wir dann die Äquivalenzrelation, Äquivalenzklasse und Zerlegung einer Menge definieren. Diese drei Begriffe werden wir im letzten Abschnitt untersuchen und nützliche Sätze beweisen.
Andere Eigenschaften von Relationen findest du in diesem Artikel.
Einführendes Beispiel
Oftmals verhalten sich verschiedene Objekte in bestimmten Aspekten gleich oder besitzen gleiche, beziehungsweise sehr ähnliche Eigenschaften.
Beispielsweise besitzen Exemplare von Büchern derselben ISB-Nummer denselben Inhalt und Autor.
Weiterhin ist das Ergebnis einer Drehung von dasselbe wie bei einer Drehung von .
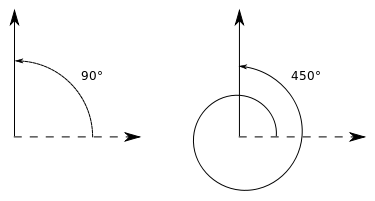
In diesem Kapitel wirst du die mathematischen Werkzeuge kennen lernen, mit denen du solche Äquivalenzen zwischen Objekten einer Grundmenge sauber beschreiben kannst.
Eine Beziehung, die die Gleichwertigkeit zwischen Objekten unter bestimmten Aspekten ausdrückt, wird Äquivalenzrelation genannt.
Wir werden sehen, dass folgende Relation auf der Grundmenge aller bisher gedruckter Buchexemplare eine Äquivalenzrelation ist:
Betrache die nebenstehende Menge mit acht Buchexemplaren und eingezeichneter Äquivalenzrelation " und besitzen dieselbe ISB-Nummer“ als Pfeildiagramm.
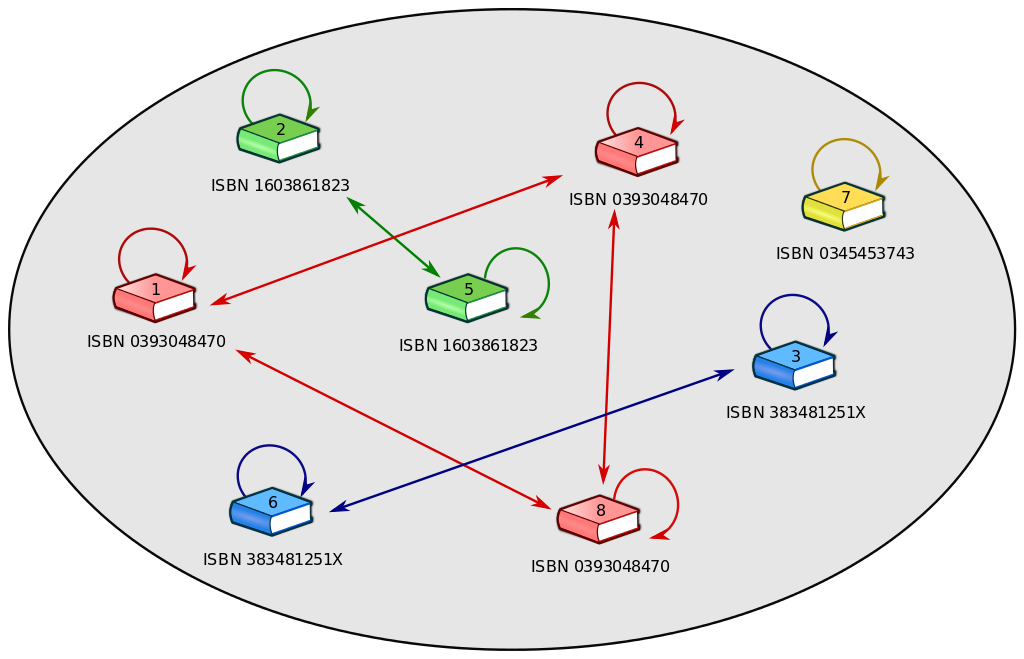
Wir werden sehen, dass die Eigenschaften der Reflexivität, Symmetrie und Transitivität der obigen Relation genau diejenigen sind, die hinreichend und notwendig für eine Äquivalenzrelation sind.
Es gibt eine weitere Möglichkeit Äquivalenzrelationen zu beschreiben: Die Möglichkeit die Grundmenge in verschiedene disjunkte Teilmengen zu zerlegen.
Nehmen wir wieder das obige Beispiel mit den Büchern. Stell dir vor, wir fassen alle Exemplare in eine Menge zusammen, die dieselbe ISB-Nummer besitzen.
Es kommen also genau dann zwei Bücher x und y in dieselbe Menge, wenn sie dieselbe ISB-Nummer besitzen, wenn also x in Relation zu y steht. Eine so entstandene Teilmenge werden wir später Äquivalenzklasse nennen.
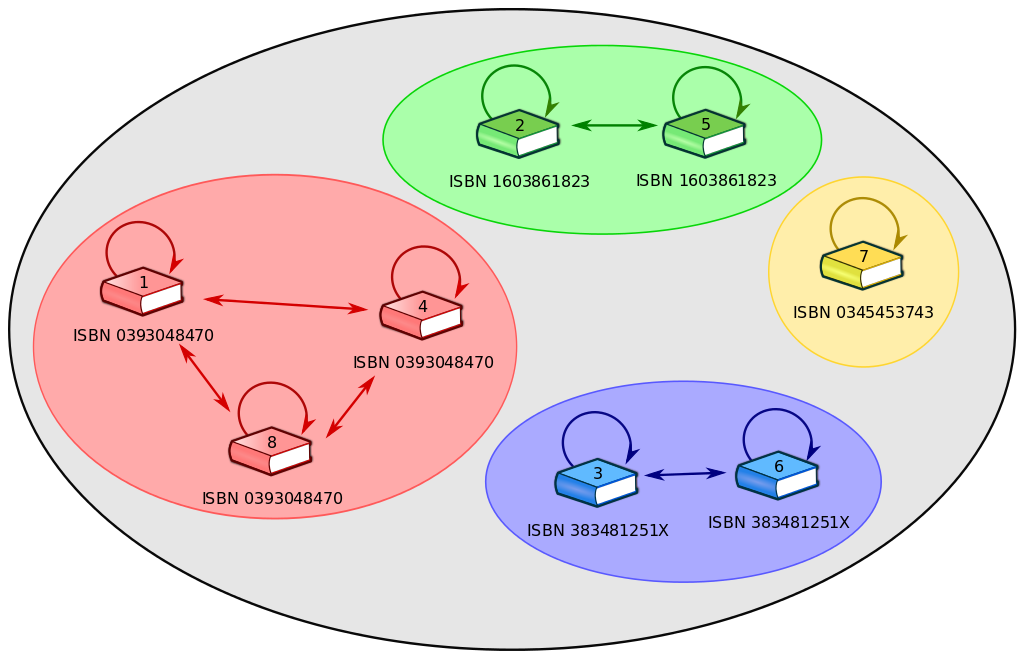
Das Ergebnis ist eine Zerlegung der Grundmenge aller gedruckter Buchexemplare in disjunkte Teilmengen. Jede dieser Teilmengen steht für ein konkretes Schriftwerk eines Autors. Denn jede ISB-Nummer bezeichnet eindeutig ein solches Schriftwerk und jede Teilmenge enthält genau diejenigen Exemplare, die dieselbe ISB-Nummer besitzen.
Man kann diese Teilmengen nun als neue Objekte betrachten. Dadurch erhältst du die Menge aller Schriftwerke. Jedes Schriftwerk ist dabei als Menge, nämlich der Menge aller Exemplare dieses Schriftwerks, modelliert. Durch eine Zerlegung einer Menge mithilfe einer Äquivalenzrelation können also neue Objekte modelliert werden (dies ist eine gängige Vorgehensweise in der Mathematik).
Definitionen
Äquivalenzrelation
Eine Äquivalenzrelation ist folgendermaßen definiert:
Definition: (Äquivalenzrelation) Eine Äquivalenzrelation ist eine homogene, binäre Relation auf einer Grundmenge, die folgende Eigenschaften besitzt:
reflexiv
symmetrisch
transitiv
Zwei Elemente, die bezüglich einer Äquivalenzrelation in Relation stehen, heißen ''äquivalent''. Wenn zwei Elemente und äquivalent zueinander bezüglich einer Äquivalenzrelation sind, schreibt man oft oder einfach anstatt der sonst üblichen Schreibweise beziehungsweise .
Äquivalenzklasse
Im obigen Beispiel haben wir durch die Äquivalenzrelation die Grundmenge in disjunkte Teilmengen zerlegt, indem wir alle Buchexemplare in einer Teilmenge zusammengefasst haben, die in Relation steht. Eine solche Teilmenge wird ''Äquivalenzklasse'' genannt und mit bezeichnet:
Eine Äquivalenzklasse ist die Menge aller Elemente der Grundmenge , die zum Element äquivalent sind:
Wenn du die Relation explizit angeben musst, kannst du auch schreiben. Es ist dann
Das Element in der Schreibweise nennt man ''Repräsentant'' oder ''Vertreter''. Ist unsere obige Definition für Äquivalenzklassen korrekt im Sinne, dass wenn und äquivalent zueinander sind? Dies beantwortet der folgende Satz:
Es gilt auch die Umkehrung des obigen Satzes:
Zusammen ergeben die vorherigen beiden Sätze folgenden wichtigen Satz:
Für Äquivalenzklassen und deren Vertreter gilt folgender Zusammenhang:
Zerlegung einer Menge
Oft haben wir bereits von der Zerlegung einer Menge gesprochen (welche in der Mengenlehre auch Partition genannt wird). Hier die Definition der Zerlegung einer Menge (im nächsten Abschnitt werden wir den Zusammenhang zwischen Äquivalenzrelation und der durch ihr definierten Zerlegung untersuchen):
Definition:(Zerlegung einer Menge) Eine Zerlegung einer Menge ist eine Menge von Teilmengen von , so dass
die Vereinigung aller Mengen von die Menge ergibt:
alle Mengen von paarweise disjunkt sind:
alle Mengen von nicht leer sind:
Zusammenhang zwischen Äquivalenzrelationen und der Zerlegung einer Menge
Wollen wir nun den Zusammenhang zwischen Äquivalenzrelationen und der Zerlegung einer Menge untersuchen.
Im einführenden Beispiel haben wir gesehen, dass eine Äquivalenzrelation eine Zerlegung der Grundmenge definiert, indem man alle äquivalenten Elemente in einer Teilmenge, der Äquivalenzklasse, zusammenfasst. Eine solche Zerlegung einer Menge durch eine Äquivalenzrelation wird mit bezeichnet und in bestimmten Kontexten der Mathematik ''Quotientenraum'' oder ''Faktorraum'' genannt. Die Zerlegung der Grundmenge ist also:
Doch ist dies wirklich eine Zerlegung im Sinne der obigen Definition? Beweisen wir es:
Satz: (Äquivalenzrelationen induzieren eine Zerlegung)
Sei eine Äquivalenzrelation auf der Grundmenge . Dann ist die Menge aller Äquivalenzklassen eine Zerlegung der Grundmenge.
Doch wie sieht es umgekehrt aus? Kannst du aus einer vorgegebenen Partition einer Menge so eine Äquivalenzrelation definieren, dass ist?
Satz: (Jede Zerlegung induziert eine Äquivalenzrelation)
Sei eine Menge und eine Zerlegung dieser Menge. Dann gibt es genau eine Äquivalenzrelation , die diese Zerlegung induziert, für die also ist. Diese Äquivalenzrelation ist definiert durch:
Dieses Kapitel basiert auf dem Artikel "Äquivalenzrelation" der freien Lehrbuchreihe „Mathe für Nicht-Freaks“. Die Autoren des Artikels kann der Versionsgeschichte entnommen werden. Dieser Kapitel steht wie das Original unter einer CC-BY-SA 3.0 Lizenz.
