Mit der schriftlichen Division werden zwei Zahlen dividiert, die zu groß für eine Rechnung im Kopf sind.
Bei der schriftlichen Division arbeitet man Stelle für Stelle des Dividenden ab und prüft, wie oft der Divisor in diesen Teil des Dividenden hineinpasst.
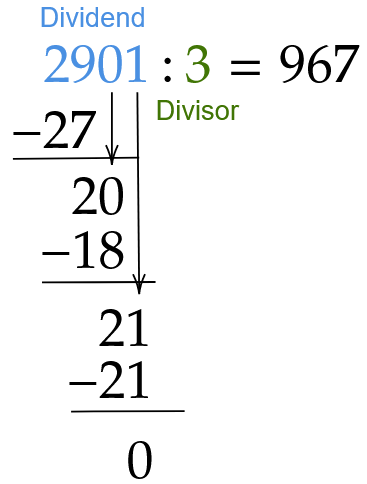
Beispiel für die schriftliche Division
Videoerklärung zur schriftlichen Division
Schriftliche Division am Beispiel
Mit dem Applet kannst du dir jeden Schritt des Beispiels genauer ansehen. Klicke es an:
Bei der Division ist zum Beispiel nicht gleich klar, wie oft der Divisor 17 den Dividenden teilt.
Hier hilft die 17-er Reihe als kleine Nebenrechnung:
Damit kann die Division selbst einfacher berechnet werden:
Division mit Rest am Beispiel
Der Divisor teilt den Dividenden nicht immer "ganz".
Bei dieser Division bleibt am Ende ein Betrag übrig, den wir Rest nennen.
Übungsaufgaben
Laden
