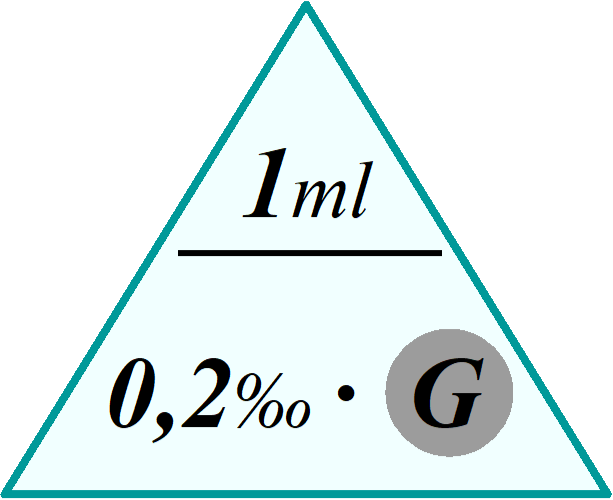Aufgaben zur Promillerechnung
Lerne hier mit Promille zu rechnen. Du liest unter anderem wichtige Informationen in Sachaufgaben heraus und rechnest Promille und Prozentangaben um.
- 1
Frau Miller trinkt auf einer familiären Silvesterparty alkoholische Getränke und nimmt dadurch 1 ml puren Alkohol zu sich. Sie misst ihren Alkoholpegel mit einem Messgerät. Das Messgerät zeigt einen Wert von 0,2 Promille an. Dadurch kann sie das Volumen ihres Blutes errechnen. Wie viel Blut fließt durch ihren Körper?
Liter - 2
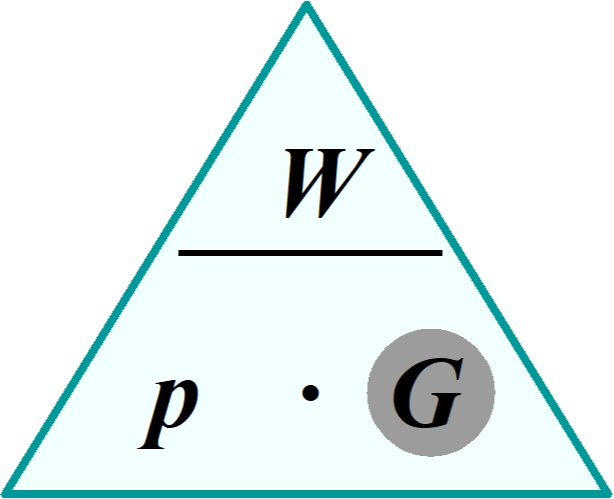
Ein Haus besitzt eine Versicherungssumme von 250.000 €. Jedes Jahr bekommt der Hausbesitzer eine Prämie von 2 ‰. Berechne die jährliche Prämie in Euro.
€ - 3
Rechne folgende Prozentangaben oder Dezimalzahlen in Promille um.
z.B.
5%
87%
- ‰
- ‰
- ‰
- ‰
- ‰
- ‰
- ‰
- ‰
- ‰
- ‰
- 4
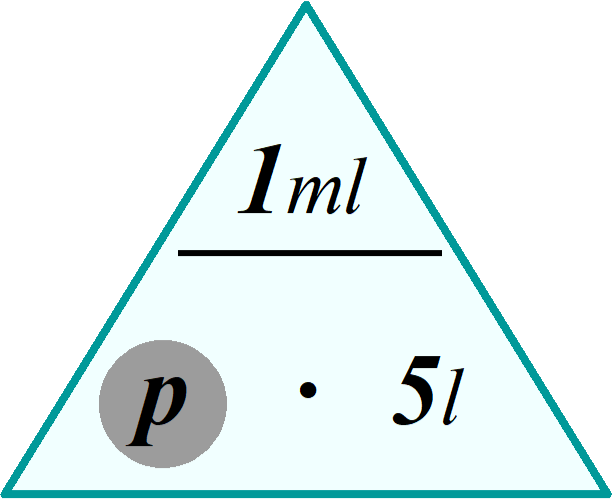
Frau Miller feiert ein Jahr später wieder mit ihren Eltern Silvester. In der Zwischenzeit ist das Messgerät kaputt gegangen. Sie weiß jedoch, dass sie insgesamt 1 ml puren Alkohol zu sich genommen hat. Ihr Blutvolumen beträgt 5 Liter. Wie hoch ist der Promilleanteil Alkohol in ihrem Blut?
‰ - 5
Frau Millers Alkoholpegel beträgt 0,2 Promille. Sie hat 5 Liter Blut im Körper. Diese werden als Grundmenge verwendet. Wie hoch ist die Menge Alkohol im Blut?
ml - 6
Die Tablette eines Medikaments wiegt insgesamt 200 mg. Davon sind 0,150 mg Wirkstoff. Wie viel Promille macht der Wirkstoff aus?
‰ - 7
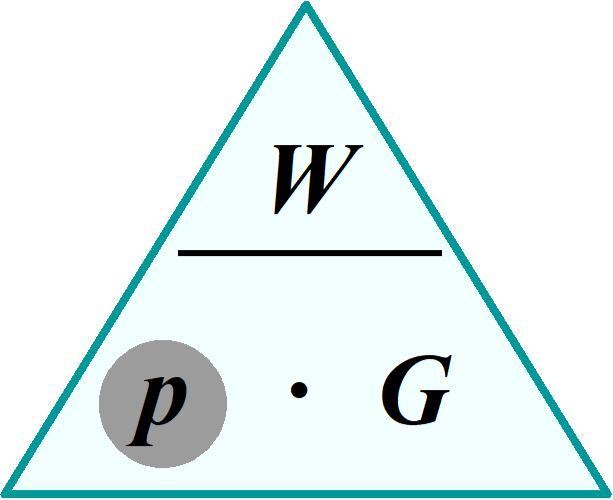
Bei Ringen aus Platin findet man häufig die Gravur 600. Das bedeutet, dass der Ring zu 600 ‰ aus Platin besteht. Der Rest enthält zum Beispiel Silber oder Palladium. Ein solcher Ring wiegt 12 Gramm. Berechne das Gewicht des Platinanteils vom Ring.
g - 8
Schreibe folgende Promilleangaben in Prozent und als Dezimalzahl.
z.B.
- 9
Bei einer Straße, die auf einen Berg führt, beträgt das Gefälle 7 ‰. Der zu überwindende Höhenunterschied ist 14 Meter. Berechne die Streckenlänge.
m - 10
Julia kauft sich ein Auto im Wert von 27.500 €. Jedes Jahr erhält sie eine Prämie im Wert von 55 €. Berechne die Versicherungsprämie in ‰.
‰
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?