Der Maßstab gibt ein Verhältnis an, in dem z. B. eine Karte zur Wirklichkeit steht. Je nach Größe der Karte ist der Maßstab anders gewählt. In dem rechten Bild hat man zum Beispiel einen Maßstab von "1 zu 15 500 000".
Mit einem Maßstab rechnen
Die Angabe eines Maßstabs 1:500 in einer Karte bedeutet:
1:500 bedeutet aber auch:
Und natürlich auch in jeder anderen Längeneinheit!
Also kann man folgendermaßen mithilfe des Maßstabs rechnen:
Länge in der Karte = Länge in der Wirklichkeit dividiert durch 500
Der Maßstab ist keine Zahl, sondern ein Verhältnis (z.B.: 1:500). Man kann deshalb nicht "mit dem Maßstab multiplizieren" oder "durch den Maßstab teilen", da man nicht durch ein Verhältnis teilen kann.
Typische Aufgaben und Beispiele
Bei einer Aufgabe, in der es um Maßstab und das Rechnen mit dem Maßstab geht, gibt es drei Größen, die eine Rolle spielen:
die Länge der Strecke in Wirklichkeit
die Länge der Strecke auf der Karte
der Maßstab der Karte.
Wenn zwei der drei Größen angegeben sind, kann man die dritte Größe ausrechnen. Wie das jeweils geht, wird in den folgenden Beispielen gezeigt.
1. Aufgabentyp: Die echte Länge ausrechnen
Gegeben ist
die Länge der Strecke in der Karte
der Maßstab der Karte
Gesucht ist
die Länge der Strecke in Wirklichkeit
Beispiel
Gegeben ist eine Karte mit dem Maßstab 1 : 20 000 000. Die gesuchte Entfernung auf dem Plan beträgt 2 cm. Wie weit sind die Orte in Wirklichkeit entfernt?
Da man mit 40 000 000 cm nicht viel anfangen kann, rechnet man diese Länge in geeignetere Einheiten um.
Die Rechenstrategie ist also:
Multipliziere die Länge in der Karte mit der zweiten Zahl des Maßstabs (1 : 20 000 000).
Wandle in sinnvolle Einheiten um (meistens Kilometer)
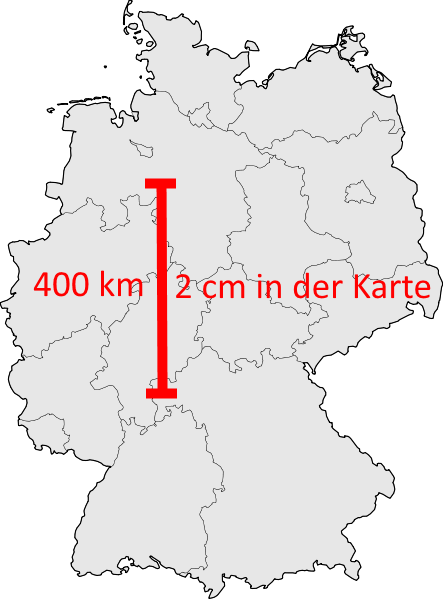
2. Aufgabentyp: Die Länge auf der Karte ausrechnen
Gegeben ist
die Länge der Strecke in Wirklichkeit
der Maßstab der Karte
Gesucht ist
die Länge der Strecke auf der Karte
Beispiel
Zwei Orte liegen in Wirklichkeit 100 km voneinander entfernt. Die Karte, auf der die Länge bestimmt werden soll, besitzt den Maßstab 1 : 500 000.
Um besser weiterrechnen zu können, wandelt man die km in cm um:
Damit ist die Entfernung in der Karte:
Die Rechenstrategie ist also:
Wandle die echte Länge in Zentimeter um
Teile diese Länge durch die größere Zahl des Maßstabs
3. Aufgabentyp: Den Maßstab der Karte ausrechnen
Gegeben ist
die Länge der Strecke in der Karte
die Länge der Strecke in Wirklichkeit
Gesucht ist
der Maßstab der Karte
Beispiel
Zwei Orte sind in der Wirklichkeit 200 km voneinander entfernt. Auf der Karte beträgt die Distanz nur 10 cm, welcher Maßstab wird in der Karte verwendet?
Um besser weiterrechnen zu können, wandelt man die km in cm um:
10 cm auf der Karte entsprechen also den 200 km = 20 000 000 cm in der Wirklichkeit
Damit ist der Maßstab 10 : 20 000 000 und das entspricht dem Maßstab 1 : 2 000 000.
Rechenstrategie ist also:
Wandle die Längen in eine gemeinsame Einheit um (hier Zentimeter)
Setze die Länge auf der Karte in ein Verhältnis zur Länge in Wirklichkeit und teile beides durch das kleinere (hier teile beides durch 10, weil 10 kleiner ist als 20 000 000)
Maßstäbe bei Vergrößerungen
Unter anderem in der Biologie werden häufig Dinge mithilfe eines Mikroskops vergrößert. Wie stark die Vergrößerung ist, wird meistens in Form eines Maßstabs angegeben. Der Maßstab 20:1 bedeutet:
Aber natürlich auch in jeder anderen Längeneinheit, also zum Beispiel:
20 mm im Mikroskop entsprechen 1 mm in der Wirklichkeit

Da das Mikroskop vergrößert und nicht wie eine Karte verkleinert, funktioniert die Umrechnung zwischen vergrößertem Bild und der Wirklichkeit genau andersherum wie bei einer Karte:
1. Beispiel: Die echte Größe einer Laus ausrechnen
Eine Laus erscheint durch das Mikroskop 10 cm groß. Eingestellt wurde das Mikroskop auf eine Vergrößerung im Maßstab 20 : 1. Wir berechnen die tatsächliche Länge:
Man teilt die Länge im Mikroskop durch die erste Zahl des Maßstabs:
Die Laus besitzt eine tatsächliche Länge von 5 mm.
Die Rechenstrategie ist also:
Überlege, wie viel kleiner etwas im Mikroskop ist als in Wirklichkeit (hier 20 mal).
Teile die Länge im Mikroskop durch diese Verkleinerung (hier Länge geteilt durch 20).
2. Beispiel: Die Größe einer Laus unter dem Mikroskop ausrechnen
Die Laus ist in Wirklichkeit 1 mm groß. Ein Mikroskop wird auf den Vergrößerungsmaßstab 15:1 eingestellt, wie groß erscheint die Laus jetzt?
Man rechnet die Länge in Wirklichkeit mal die erste Zahl des Maßstabs:
Die Rechenstrategie ist also:
Überlege, wie stark das Mikroskop etwas vergrößert (hier 15 mal).
Rechne die Länge im Mikroskop mal diese Vergrößerung (hier Länge mal 15).
3. Beispiel: Den Maßstab eines Mikroskops ausrechnen
Die Länge einer Laus beträgt in Wirklichkeit 5 mm. Dieselbe Laus wird durch das Mikroskop auf eine Größe von 10 cm vergrößert. Gesucht ist der Maßstab, mit dem das Mikroskop ein Objekt vergrößert.
Zum einfacheren Rechnen wandelt man die cm in mm um:
100 mm im Mikroskop entsprechen also 5 mm in der Wirklichkeit
Der Maßstab entspricht also dem Verhältnis 100 mm : 5 mm und man erhält als Maßstab
20 : 1.
Die Rechenstrategie ist also:
Wandle die Längen in eine gemeinsame Einheit um, um besser rechnen zu können.
Setze Länge in Wirklichkeit : Länge im Mikroskop als das Verhältnis des Maßstabs und teile dann beides durch das kleinere (hier: teile beides durch 5, weil 5 kleiner ist als 100).
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Thema Maßstab
