Zwischen zwei Körpern mit unterschiedlicher Ladung herrscht eine elektrische Spannung.
Die Spannung zwischen zwei Punkten A und B ist diejenige Energiemenge bzw. Arbeit, die benötigt wird, um eine Ladungseinheit von A nach B zu transportieren. Damit gibt uns die Spannung ein Größenverhältnis an wie "stark" der Strom einer Stromquelle ist.
Artikel in Arbeit
Spannung () = Arbeit () pro Ladung ()
(mit Spannung , Arbeit und Ladung )
Einleitung
Wir nehmen uns ein modellhaftes Beispiel, um die prinzipiellen Schritte zu verstehen und wichtige Begriffe kennenzulernen. Mit dem Schieberegler unten kannst du die einzelnen Schritte sehen.
1. Zwei isolierte Kugeln
Für den Anfang haben wir zwei isolierte ungeladene Metallkugeln. Sie sind nach außen elektrisch neutral.
2. Gleich viele Ladungen
Die Metallkugeln besitzen jedoch positive und negative Ladungsträger. Da die Anzahl ausgeglichen ist, hebt sich die Ladung nach außen auf. Bei Metall sollte außerdem bekannt sein, dass die Elektronen frei beweglich sind und die Protonen fest im Kern "sitzen".
3. Ladungstrennung
Durch Wegnahme von Elektronen wird die erste Kugel positiv aufgeladen.
4. Elektronentransfer
Durch Aufbringen von Elektronen wird die zweite Kugel negativ aufgeladen.
5. Pol
Von Außen betrachtet haben wir nun einen positiven und negativen Pol (Plus- und Minuspol). Es herrscht eine Spannung zwischen den beiden Körpern.
6. Stromfluss
Verbindet man die beiden Kugel durch einen Leiter so fließt Strom, bis sich die Ladung wieder gleich verteilt hat.
Elektrische Spannung entsteht durch Trennung von Ladungen.
Vergleich von elektrischer Spannung und potentieller Energie
Betrachten wir die Größe genauer. Dafür nehmen wir uns zwei unterschiedliche Ladungen vor. Analog vergleichen wir die potentielle Energie im Gravitationsfeld, die aus der Mechanik bekannt ist.
Elektrische Spannung | Potentielle Energie |
|---|---|
Zwischen zwei entgegengesetzten Ladungen wirkt eine Anziehungskraft. Um die beiden Ladungen zu trennen müssen wir daher eine Kraft aufwenden. | Durch die Gravitationskraft der Erde werden Gegenstände angezogen, so dass wir ebenso hier eine Kraft aufwenden müssen um z. B. eine Tafel Schokolade anzuheben. |
Üben wir diese Kraft über einen bestimmten Weg aus, so wird Arbeit geleistet. | Diese Arbeit ist vergleichbar mit der Hubarbeit . |
Wenn die Kraft nicht mehr wirkt, wird sich die Ladung, falls möglich, zurückbewegen (Strom fließt). | Lassen wir der Körper los, so fällt er und verliert an potentieller Energie. |
Die dabei abgegebene Energie entspricht | Mechanisch: |
Je höher die Spannung ist desto mehr Arbeit wird geleistet.
Potentialdifferenz
Wir betrachten zwei Punkte und in einem homogenen elektrischen Feld z. B. eines Plattenkondensators. Dort herrschen jeweils die Potentiale und . Die Spannung ist dann:
Herleitung
(In diesem Abschnitt fehlen noch Zeichnungen.)
Auf eine Ladung in einem elektrischen Feld mit der Feldstärke wirkt die Kraft
Nun soll die Ladung um die Strecke bewegt werden. Die Arbeit, die dabei verrichtet wird, ist . Aus der Mechanik ist bereits bekannt, dass (Arbeit = Kraft mal Weg) ist.
Wir stellen fest: Besaß die Ladung im Punkt 1 die Energie , so hat sich nun die Energie erhöht auf , wobei die Arbeit, die geleistet wurde, beträgt.
Wenden wir die Definition der Spannung an so erhalten wir:
Mit der Definition des elektrischen Potentials folgt daraus
Art der Ladungstrennung
In der Einleitung haben wir gesehen, dass Spannung durch Ladungstrennung erzeugt werden kann. Hier sind einige Beispiele, wie solch eine Trennung zustande kommt.
Ursache | Vorgang | Anwendung |
|---|---|---|
Reibung | Reibung von Isolierstoffen | Bandgenerator, Trennung von Stoffen (z. B. Kunststoff). Häufig aber unerwünschter Effekt in der Technik. |
Chemische Reaktion | Zwei Leiter werden in eine leitende Flüssigkeit getaucht | Autobatterie, Akkumulator, Batterien |
Induktion | Bewegung von Leitern im Magnetfeld | Generator in Kraftwerken, Fahrraddynamo |
Formeln und Berechnungen
Formelzeichen | Spannung | |
|---|---|---|
SI-Einheit | Volt | |
Formel | Arbeit pro Ladung |
Schaltsymbole
Schaltsymbol | Beschreibung |
|---|---|
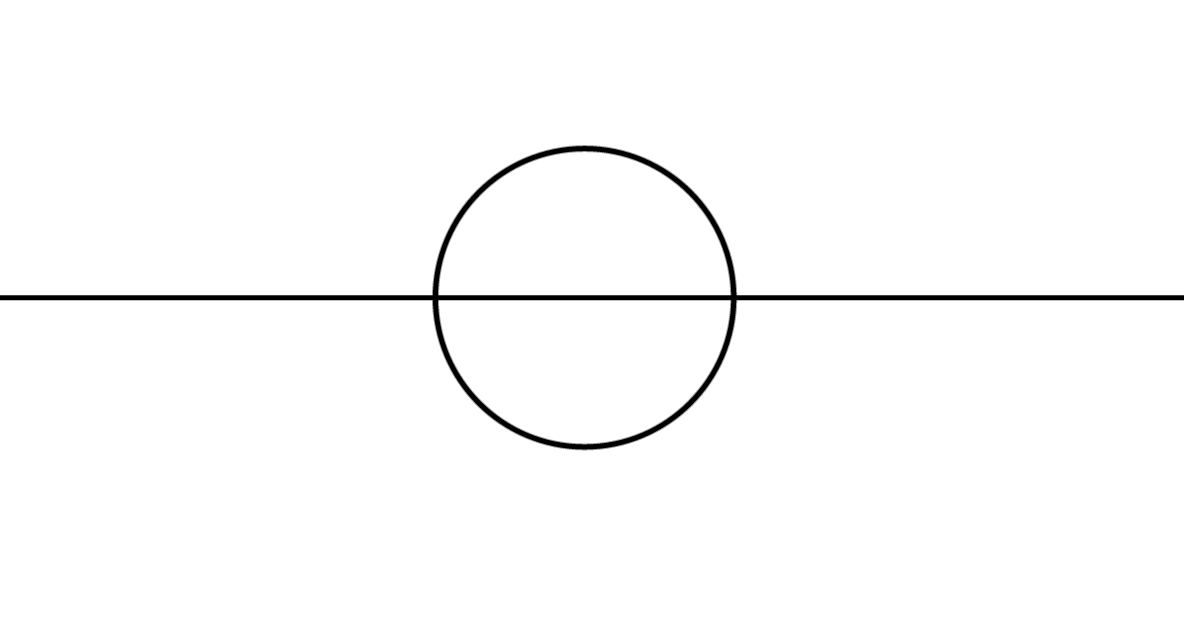 | Spannungsquelle Gleichstrom nach DIN-Norm |
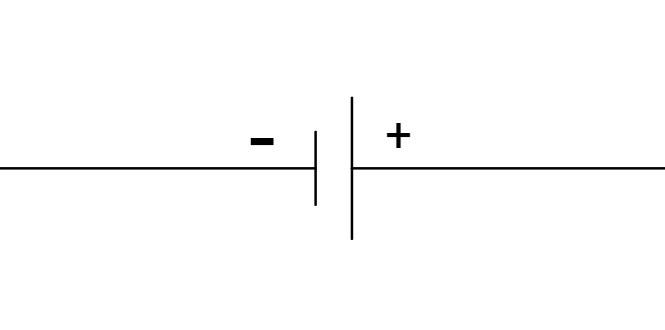 | Schaltsymbol Akkumulator |
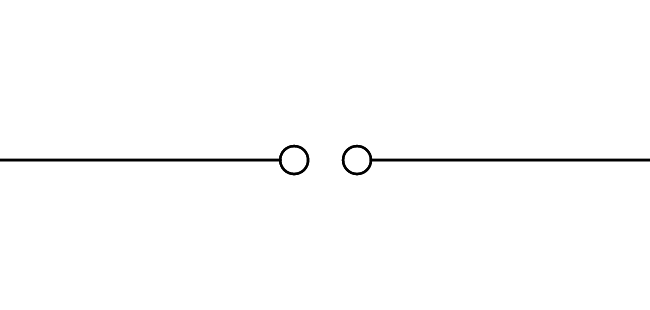 | Spannungsquelle Gleichstrom |
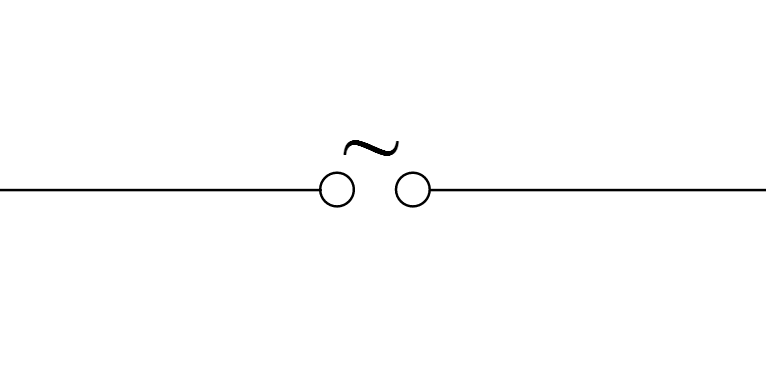 | Spannungsquelle Wechselstrom |
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
