Benannt ist dieser 1922 untersuchte Effekt nach seinem Entdecker Arthur Holly Compton. Es handelt sich dabei um das Phänomen, dass elektromagnetische Strahlung seine Wellenlänge bei Streuung an Elektronen ändert. Der Compton-Effekt dient damit als wichtiger Nachweis der Teilcheneigenschaften von Photonen.
Experimenteller Aufbau und Ablauf
A. H. Compton führte seine Experimente mit Röntgenstrahlung und Graphit durch. Dazu bestrahlte er einen Streukörper aus Graphit mit Röntgenstrahlen einer bekannten Wellenlänge und maß die Wellenlänge der gestreuten Strahlung in Abhängigkeit des Streuwinkels .
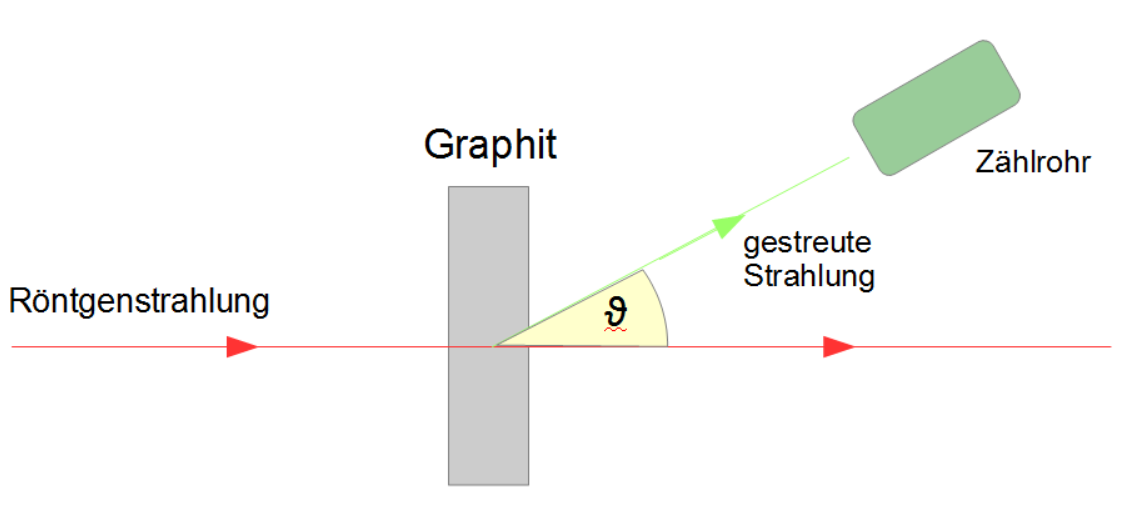
Abb. 1: Schematischer Aufbau zur Beobachtung des Compton-Effekts
Beobachtungen
Streustrahlung beinhaltet ursprüngliche Wellenlänge und eine neue Wellenlänge
je größer der Streuwinkel , desto größer der Wellenlängenunterschied
unabhängig von der Wellenlänge der Ausgangstrahlung, ausschleßlich von abhängig
unabhänigig vom Streukörper
Erklärung
Die Beobachtungen des Compton-Effektes lassen sich mit Hilfe von Stoßvorgängen erklären. Hierbei treten zwei verschiedene Arten auf. Das Photon der Röntgenstrahlung der Wellenlänge kann entweder auf ein Atom oder ein Elektron im Graphit treffen. Die Elektronen im Graphit sind dabei nur sehr schwach an die Atome gebunden und können als fast frei beweglich angesehen werden. Das Photon besitzt aufgrund seiner Wellenlänge und Frequenz eine bestimmte Energie . Trifft es nun auf ein Atom wird das Photon zwar abgelenkt, das heißt es ändert seine Richtung, aber es behält seine Energie und damit seine Wellenlänge bei. Dies geschieht aufgrund der großen Masse des Atoms. Man kann es sich vorstellen wie ein Ball, der auf eine Wand trifft. Dabei prallt er in entgegengesetze Richtung zurück, bleibt aber genauso schnell wie vorher. Dieser Stoßvorgang erklärt somit das Auftreten der ursprünglichen Wellenlänge in der gestreuten Strahlung.
Die neu zu beobachtbare Wellenlänge kann durch die zweite Stoßform erklärt werden. Hier trifft das Photon auf ein fast freies Elektron, das im Vergleich zu einem Atom eine viel geringere Masse besitzt. Bei diesem elastischen Stoß kommt es zu Energie- und Impulsübertragung. Das Elektron nimmt somit einen Teil der Energie des Photons auf und das Photon wird, wie in der Abbildung dargestellt, um den Winkel abgelenkt. Das Elektron besitzt nun eine kinetische Energie, mit der es sich nach dem Stoß bewegt. Die Energie des Photons nach dem Stoß ist somit die Differenz seiner Energie vor dem Stoß und der kinetischen Energie des Elektrons: . Wie viel Energie dabei an das Elektron übertragen wird ist abhängig von dem Winkel, unter welchem das Photon auf das Elektron trifft. Die Herleitung erfolgt über die Stoßgesetze bei nicht zentralen Stößen. Dies ergibt eine Formel für in Abhängigkeit des Streuwinkels .
Dabei ist die sogenannte Comptonwellenlänge (für Elektronen). Diese Formel zeigt deutlich, dass der Wellenlängenunterschied ausschließlich vom Streuwinkel und nicht von anderen Faktoren wie der ursprünglichen Wellenlänge abhängt.
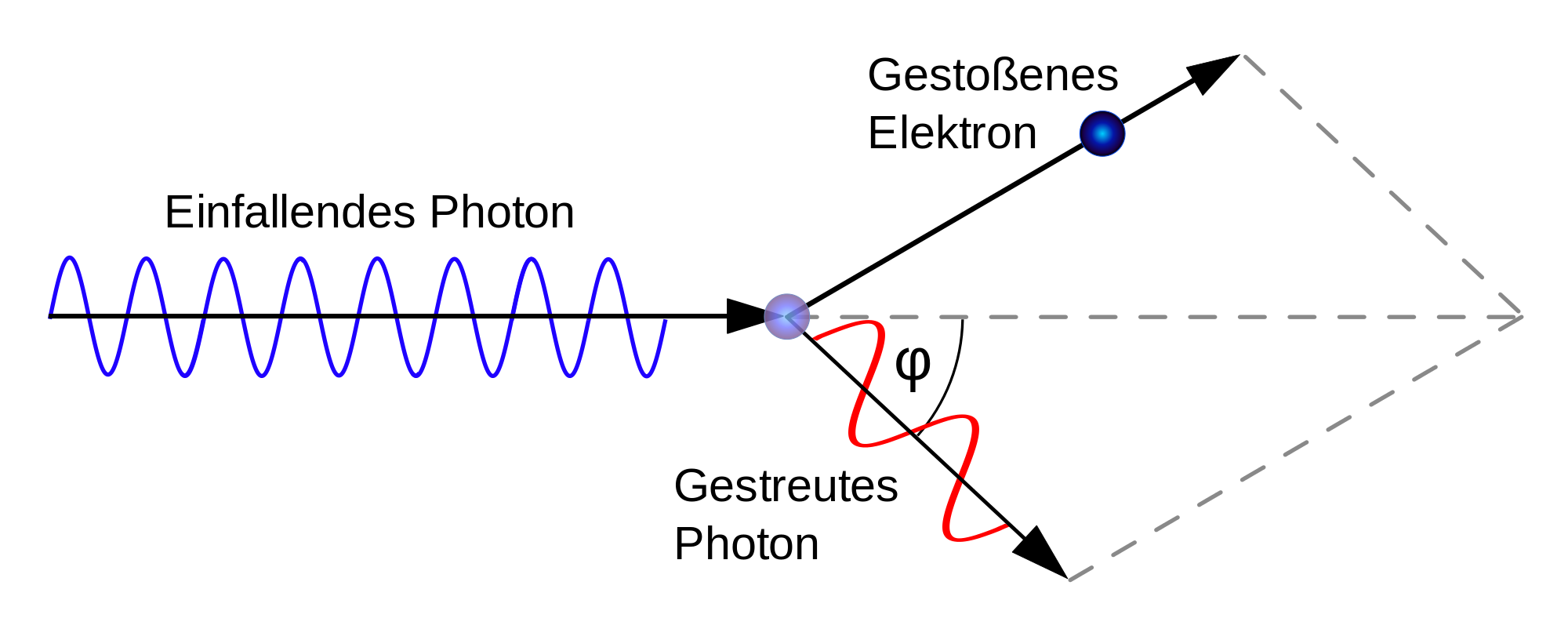
Abb. 2: Stoßprozess zwischen Photon und Elektron
Bedeutung für die Quantenmechanik
Eine Erklärung über Stöße, wie sie eben beschrieben wurde, kann nur zu den richtigen Ergebnissen führen, wenn es sich bei der einfallenden Strahlung tatsächlich um Teilchen handelt, denn Wellen sind nicht in der Lage mit Teilchen, wie den Elektronen, zu stoßen. Der Compton-Effekt belegt somit die von Einstein eingeführte Teilcheneigenschaft von Licht. Comptons Experimente waren ein wichtiger Faktor, um die neuen Ideen der Quantenmechanik in der breiten Masse der Physiker zu etablieren.
