Bei den Planungen zum Lagrange-Formalismus ergab sich die Frage, wieso die kinetische Energie ein Fixpunkt der Legendre-Transformation ist. Dieser Artikel gibt eine erste Antwort. Dabei betrachten wir den einfacheren Fall, dass wir nur ein Teilchen haben, dessen Bewegung vollständig durch Angabe einer generalisierten Koordinate beschrieben werden kann (wie beim mathematischen Pendel oder dem harmonischen Oszillator).
Erklärung
Der Impuls gibt an, wie stark sich die Bewegungsenergie durch eine Geschwindigkeitsänderung ändert (wenn die Gesamtenergie des Systems erhalten bleibt). Dieser Impuls ist streng monoton in :
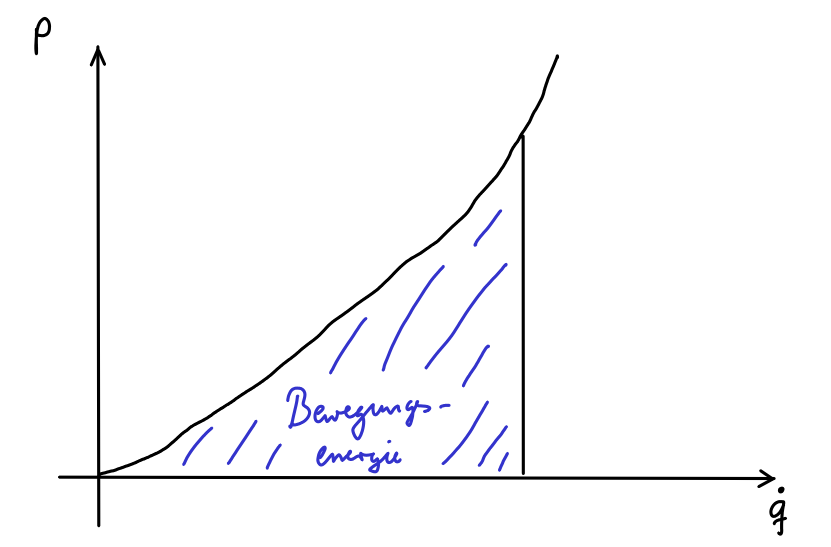
Betrachten wir eine Änderung der Geschwindigkeit:
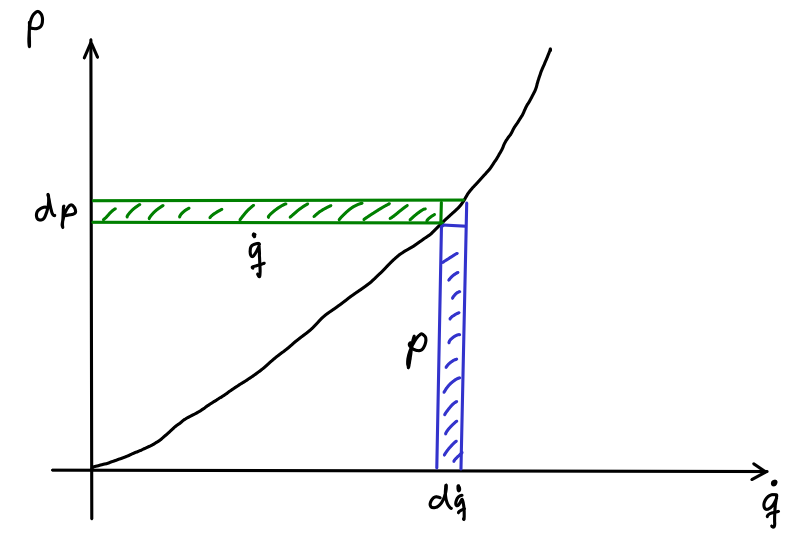
Die Rechtecksfläche gibt die Änderung der kinetischen Energie durch die Geschwindigkeitsänderung an.
Betrachten wir nun die durch gegebene Fläche. Hier ist
Wenn wir annehmen, dass wir in kartesischen Koordinaten sind, so ist und damit
Nun ist der Term gleich der Arbeit, die am Teilchen verrichtetet wird. Damit haben wir:
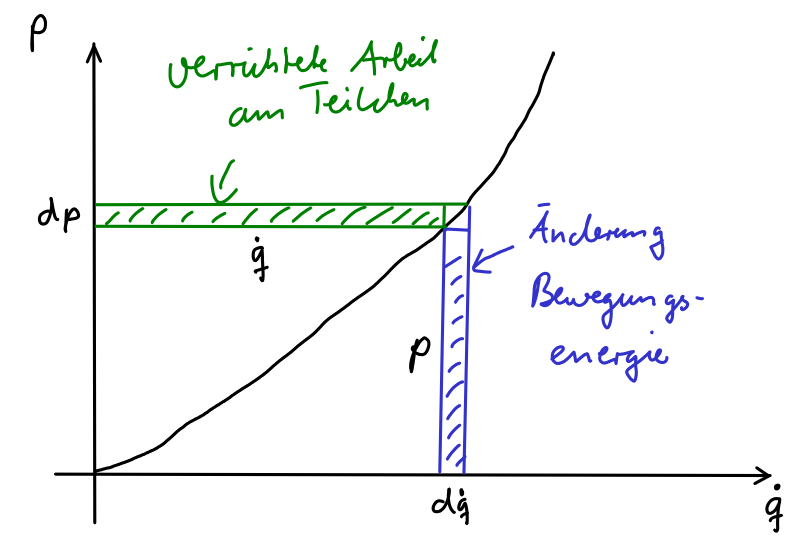
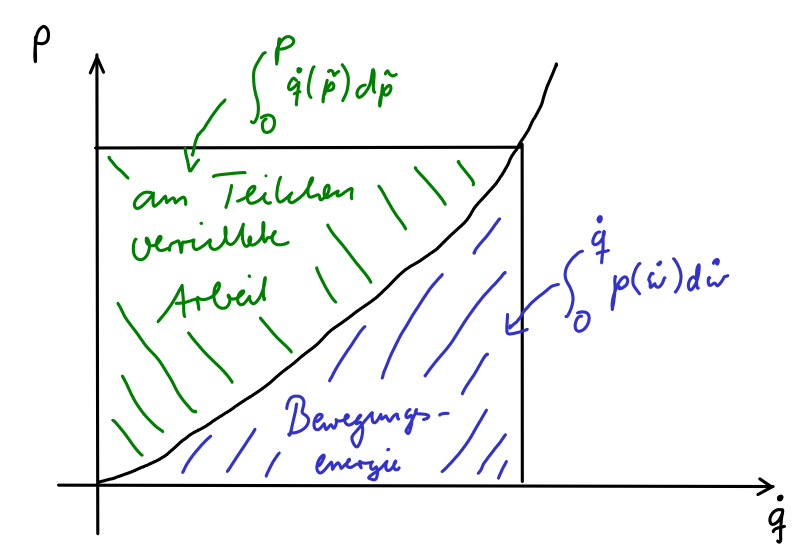
Auf der einen Seite ist gleich der kinetischen Energie des Teilchens. Wenn wir die Legendre-Transformation betrachten, so erhalen wir das Integral nach der obigen Herleitung ist dieses Integral gleich , also gleich der Arbeit, die am Teilchen verrichtet wird.
Der Term gibt also nicht die Bewegungsenergie, sondern die am Teilchen verrichtete Arbeit wieder. Aus Energieerhaltung sind beide Terme gleich.
Offene Fragen
Wie kann die Legendre-Transformation bei der Lagrange-Funktion interpretiert werden? Kann oder analog zu diesem Artikel interpretiert werden?
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
