In der Aufgabe soll eine Eigenschaft einer Integralfunktion einer ganzrationalen Funktion 2. Grades erfasst und ohne Rechnung begründet werden.

$x>3$

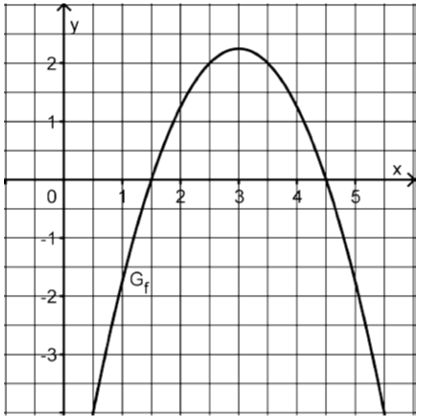
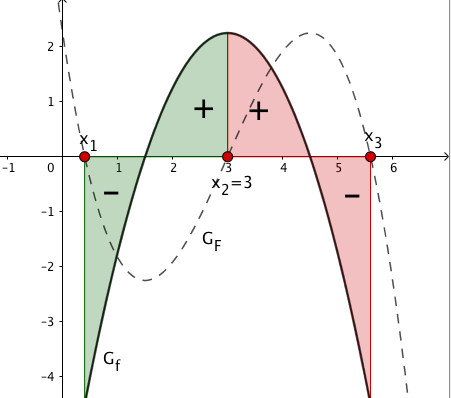
Wenn man von drei aus in positive $x$-Richtung geht , ist der Graph von $f$ positiv, daher "kommt Fläche dazu" und $F$ ist auch positiv. Ab ca. $x=\mathrm{4,5}$ ist die Fläche unter dem Graphen allerdings negativ. $F$ ist aber noch nicht an dieser Stelle negativ, sondern erst, wenn die negative Fläche betragsmäßig größer ist als die positive Fläche, die gesamte Flächenbilanz also negativ. An dieser Stelle gibt es dann eine Nullstelle ($x_1$ in der Zeichnung) und danach sinkt der Funktionswert von $F$ immer weiter, es gibt also rechts der $3$ keine weiteren Nullstellen mehr.

$x<3$

Zeit also, in der anderen Richtung nach Nullstellen zu suchen. Wenn man von $x=3$ aus in negative $x$-Richtung geht stellt auch hier fest, dass der Graph überhalb der $x$-Achse verläuft, weil man allerdings in die negative Richtung geht, wird diese Fläche nun negativ gewertet. Also ist $F$ erst negativ. Das Vorzeichen von $f$ ändert sich bei ca. $\mathrm{1,5}$ und $F$ hat eine Nullstelle, wenn die negative Fläche genauso groß ist, wie die positive Fläche (Flächenbilanz 0, $x_3$ in der Zeichnung oben), und wird danach immer größer (denke daran, weil wir in negative Richtung gehen trägt ein negativer Graph positiv zur Flächenbilanz bei), also haben wir alle Nullstellen gefunden.

$F$ hat also drei Nullstellen, eine bei $x=3$, eine bei einem kleineren $x$-Wert und eine bei einem größeren $x$-Wert. Der Ort der Nullstellen spielt aber für die Antwort keine Rolle.