Aufgabe 1
Vereinfache die folgende Schaltgleichung:
Aufgabe 2
Vereinfache die folgende Schaltgleichung:
Aufgabe 3
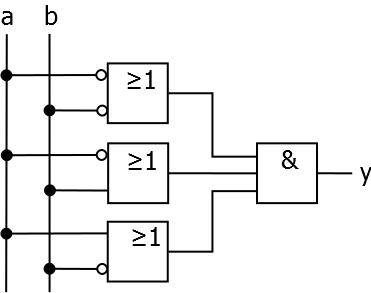
Ermittle für die angegebene Schaltung die zugehörige Schaltgleichung. Vereinfache diese anschließend weitestmöglich.
Zusatz: Versuche die vereinfachte Schaltgleichung so umzuformen, dass nur eine Sorte Logikgatter nötig ist.
Aufgabe 4
Ermittle aus der angegebenen Schaltbelegungstabelle eine Schaltgleichung. Wähle dafür eine sinnvolle Normalform.
Vereinfache diese Schaltgleichung rechnerisch mithilfe der Schaltalgebra.
Gib zu der vereinfachten Schaltgleichung eine Schaltung an.
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
