In diesem Artikel werden die Lagrange Gleichungen zweiter Art erklärt.
Die Formulierung der klassischen Mechanik nach Lagrange erlaubt es, die Bewegungsgleichungen eines mechanischen Systems mithilfe der Variationsrechnung aus dem Hamiltonschen Prinzip extremaler Wirkung herzuleiten, Ausgangspunkt ist die Lagrange-Funktion. Der Lagrange-Formalismus ist invariant unter Koordinatentransformationen, wodurch die Berücksichtigung von Zwangskräften einfacher ist als in der Newtonschen Mechanik.
Der quantenmechanische Pfadintegral-Formalismus nach Feynman basiert auf den selben Grundideen wie die Mechanik nach Lagrange.
Übersicht
Nach dem Hamiltonschen Prinzip - oft auch Prinzip der extremalen Wirkung oder etwas unpräzise Prinzip der kleinsten Wirkung genannt - wird die Dynamik jedes mechanischen Systems durch die Lagrange-Funktion
beschrieben. ist dabei die kinetische Gesamtenergie des Systems und die potentielle Gesamtenergie. Die Lagrange-Funktion hängt von den den generalisierten Koordinaten des Systems ab, sowie den generalisierten Geschwindigkeiten , auch die Zeit kann explizit in eingehen. Koordinaten und Geschwindigkeiten werden dabei als unabhängige Variablen gehandhabt.
Die Bewegungsgleichungen sind dann die sogenannten Euler-Lagrange-Gleichungen oder auch Lagrange-Gleichungen 2. Art,
Aus der Lagrange-Funktion kann der generalisierte oder kanonische Impuls
bestimmt werden. spielt eine wichtige Rolle beim Übergang zur Formulierung der Mechanik nach Hamilton, ebenso wie beim Übergang von der klassischen Physik zur Quantenmechanik.
Eigenschaften von
Schon allein aus den Überlegungen zum Hamiltonschen Prinzip und der Euler-Lagrange-Gleichung lassen sich einige nützliche Eigenschaften von formulieren.
Setzt sich ein System aus mehreren Teilsystemen zusammen, die untereinander nicht wechselwirken, ist die Lagrange-Funktion des Gesamtsystems die Summe der Lagrange-Funktionen der Teilsysteme. Das bedeutet anschaulich, dass die Bewegungsgleichungen der einzelnen Teilsysteme untereinander nicht gekoppelt sind. Die Teilsysteme entwickeln sich unabhängig voneinander.
Wird die Lagrange-Funktion eines mechanischen Systems mit einem beliebigen, konstanten Faktor multipliziert, ändern sich die Bewegungsgleichungen nicht. Damit können die Maßeinheiten der physikalischen Größen frei gewählt werden und haben keinen Einfluss auf die Dynamik des Systems. Durch die Additivität der Lagrange-Funktion wird aber festgelegt, dass in allen Teilsystemen die selben Einheiten gewählt werden müssen.
Zwei Lagrange-Funktionen und , die sich nur um die totale Ableitung einer beliebigen Funktion nach der Zeit unterscheiden, bringen die selbe Dynamik hervor, da sich die Wirkung nur um einen konstanten Zusatzterm von unterscheidet, der beim Ausführen der Variation wegfällt.
Beispiel
Der Lagrange-Formalismus soll an einem ebenen Fadenpendel demonstriert werden. Der Pendelkörper mit Masse wird durch die Aufhängung auf eine Kreisbahn mir Radius in der --Ebene gezwungen (Abb.1) und werde durch die Schwerkraft in die Ruhelage zurückgedrängt.
Da das System nur einen Freiheitsgrad hat, wird nur eine Koordinate benötigt. Hierfür bietet sich der Winkel an, der gegen die Vertikale gemessen wird. Ausgedrückt durch lautet die Tangentialgeschwindigkeit des Pendelkörpers und die kinetische Energie damit
Die potentielle Energie des Pendelkörpers im Gravitationsfeld ist
so dass die Lagrange-Funtion
lautet. Die Euler-Lagrange-Gleichung für das Fadenpendel ergibt sich aus :
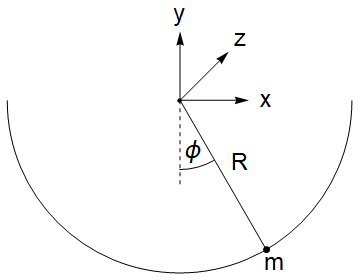

Abb.1: Ein Fadenpendel, das in einer Ebene auf eine Kreisbahn mit Radius R schwingen kann. Die Schwerkraft zeige in Richtung der negativen -Richtung.
Durch Kürzen auf beiden Seiten und die Näherung für kleine Winkel erhält man die Differentialgleichung für einen Harmonischen Oszillator mit Kreisfrequenz ,
Die Bewegungsgleichung wird gelöst durch die Funktion
Für kleine Auslenkungen führt das Fadenpendel also Oszillationen um den tiefsten Punkt der Kreisbahn herum aus. und können aus den Anfangsbedingungen bestimmt werden.
Der zum Winkel konjugierte kanonische Impuls ist der Drehimpuls
Der Vorteil der Methode nach Lagrange ist, dass keine Ausdrücke für die Kräfte oder Zwangskräfte gefunden werden müssen, um die Bewegungsgleichung aufzustellen, was sich vor allem bei komplizierten Systemen und Vielteilchensystemen auszahlt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
Quellen
- Sommerfeld, A. (1968). Vorlesungen über theoretische Physik I. Leipzig. Geest & Portig K.-G.
- Landau, L.D., Lifschitz E.M. (1997). Lehrbuch der theoretischen Physik I. Frankfurt a.M. Harri Deutsch
