Geometrie, Teil A, Aufgabengruppe 1

Für jeden Wert von $a$ mit $a\in\mathbb{R}$ ist eine Gerade $g_a$ gegeben durch

$g_a:\vec{X}=\begin{pmatrix}2\\a-4\\4\end{pmatrix}+\lambda\cdot \begin{pmatrix}2\\-2\\1\end{pmatrix},\;\lambda\in\mathbb{R}$ .

a)

(2 BE)

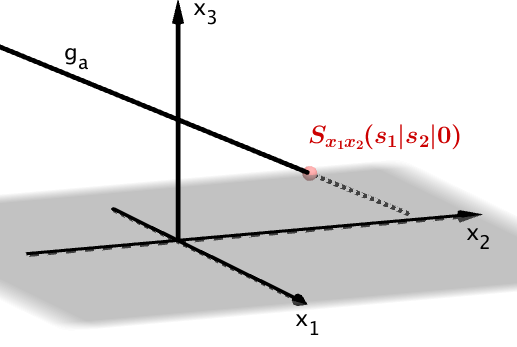
Bestimmen Sie in Abhängigkeit von $a$ die Koordinaten des Punktes, in dem $g_a$ die $x_1x_2$ -Ebene schneidet.

b)

(3 BE)

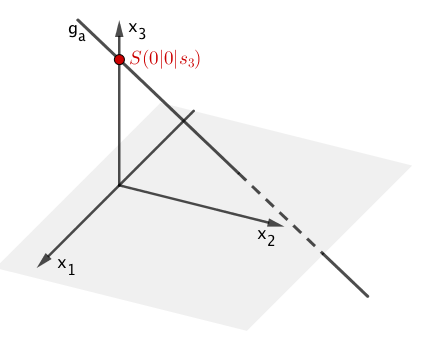
Für genau einen Wert von $a$ hat die Gerade $g_a$ einen Schnittpunkt mit der $x_3$ -Achse. Ermitteln Sie die Koordinaten dieses Schnittpunktes.