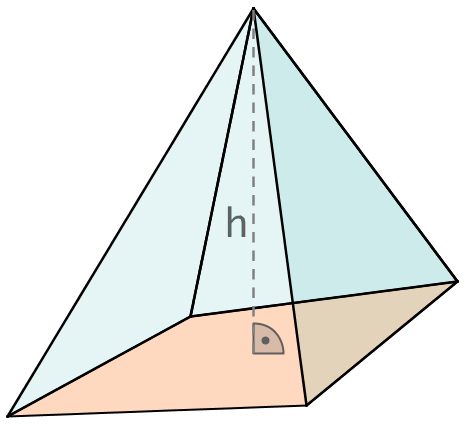
Eine Pyramide ist ein Körper, der durch Verbinden aller Ecken eines beliebigen Vielecks mit einem Punkt außerhalb der Ebene, in der das Vieleck liegt, entsteht.

Volumen

$V_\text{Pyramide} = \frac{1}{3}\cdot G \cdot h$

G: Grundfläche

h: Höhe

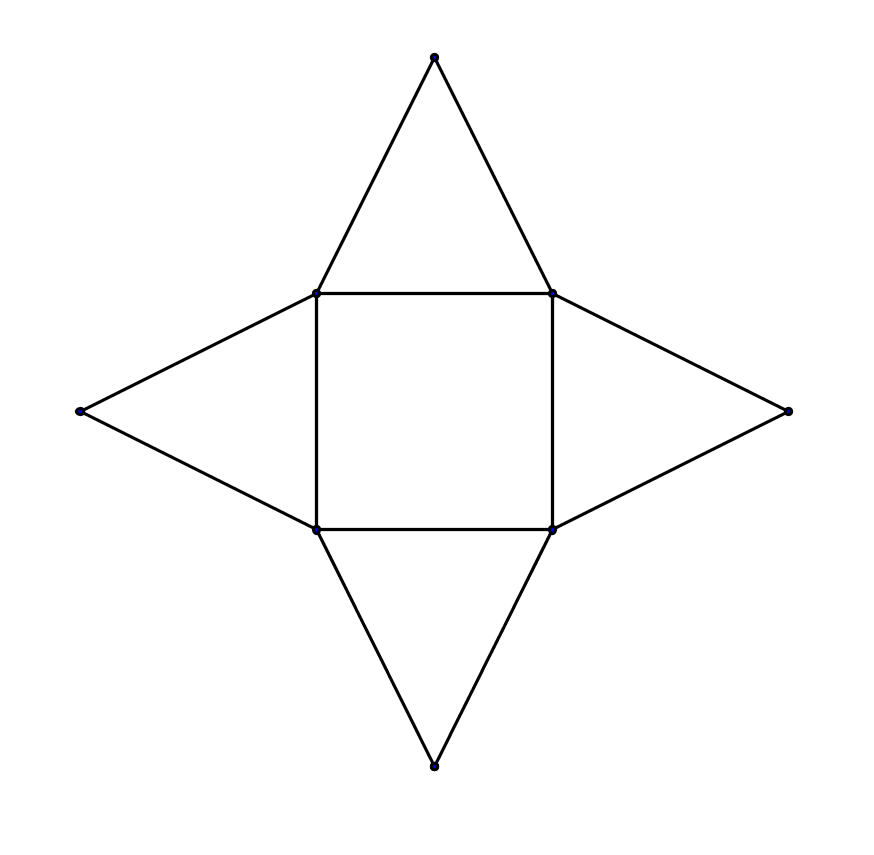
Oberflächeninhalt

$O_\text{Pyramide} = G + M$

M: Mantelfläche

Video zum Thema Oberfläche und VOlumen der Pyramide

Sonderformen der Pyramide

Bezeichnung

Eigenschaften

Beispiele

gerade Pyramide

• alle Kanten der Mantelfläche sind gleich lang

• die Spitze der Pyramide liegt senkrecht über dem Mittelpunkt der Grundfläche

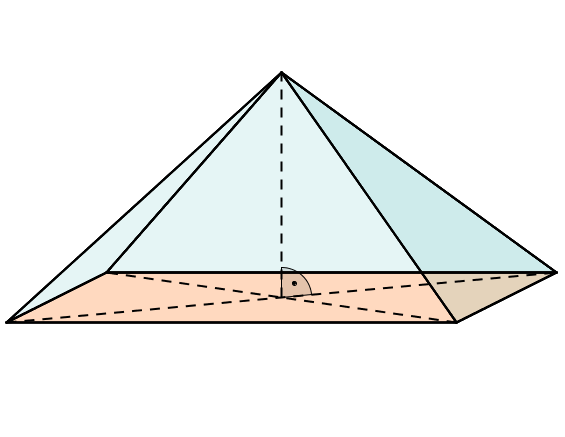
regelmäßige / reguläre Pyramide

• gerade Pyramide mit regelmäßigem Vieleck als Grundfläche

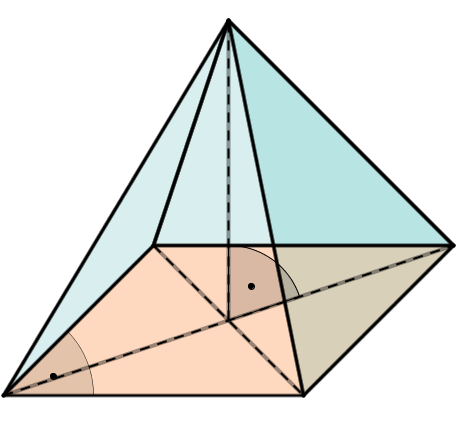
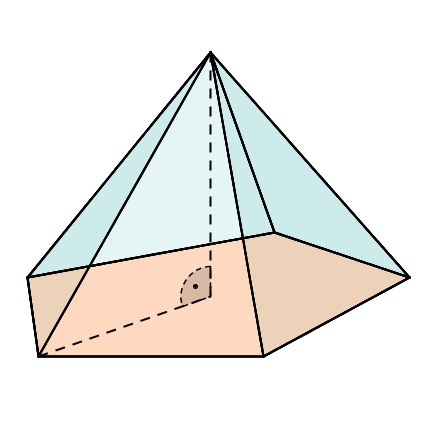
schiefe Pyramide

• Die Spitze liegt nicht genau über dem Mittelpunkt der Grundfläche.

• Sie hat das gleiche Volumen wie die gerade Pyramide mit gleicher Höhe

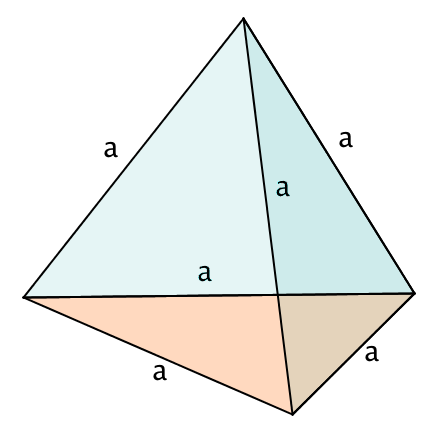
regulärer Tetraeder/36213

Pyramide, die

• vier kongruente gleichseitige Dreicke als Fläche hat

• sechs gleich lange Kanten hat

Bemerkungen

• Jede regelmäßige Pyramide ist eine gerade Pyramide. Die Umkehrung dieser Aussage ist nicht in jedem Fall richtig. Es gibt also gerade Pyramiden, die nicht regelmäßig sind (z.B. eine vierseitige Pyramide mit rechteckiger Grundfläche).

Berechnen des Volumens anderer Körper   

Im Artikel Volumenberechnung in der analytischen Geometrie/2099 findet man eine fortgeschrittenere Variante für die Berechnung des Volumens einer Pyramide. Auch das Volumen anderer Körper wird dort berechnet.